GAN对抗生成网络原始论文理解笔记
文章目录
- 论文:Generative Adversarial Nets
- 符号意义
- 生成器(Generator)
- 判别器(Discriminator)
- 生成器和判别器的关系
- GAN的训练流程简述
- 论文中的生成模型和判别模型
- GAN的数学理论
-
- 最大似然估计转换为最小化KL散度问题
- 定义 P G P_G PG
- 全局最优
论文:Generative Adversarial Nets
符号意义
- G()表示对生成器功能的一个封装函数
- D()表示对判别器功能的一个封装函数
- x表示真实数据
- z表示含噪音的数据
- x ‾ \overline x x表示G(z),将噪音数据输入到生成器得到的结果
- θ g θ_g θg表示生成器的参数
- θ d θ_d θd表示判别器的参数
- P d a t a ( x ) P_{data}(x) Pdata(x)表示真实数据分布
- P G ( x ; θ ) P_G(x;\theta) PG(x;θ)表示生成器生成的数据分布
生成器(Generator)
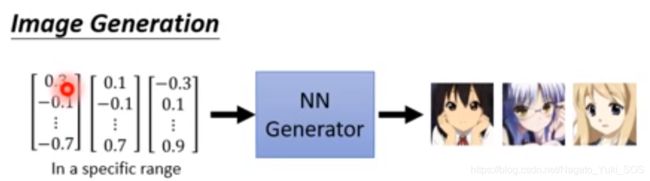
狭义的生成器就是输入一个向量,通过生成器,输出一个高维向量(代表图片、文字等)
其中输入向量的每一个维度都代表一个特征。如下图示例:
判别器(Discriminator)
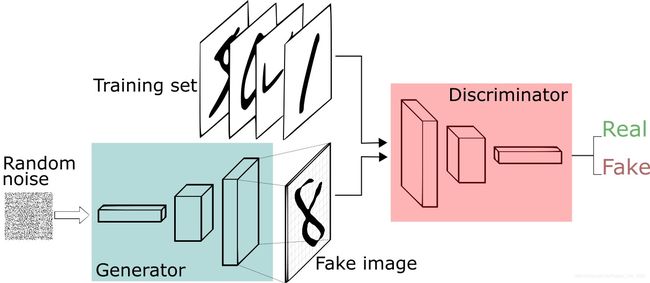
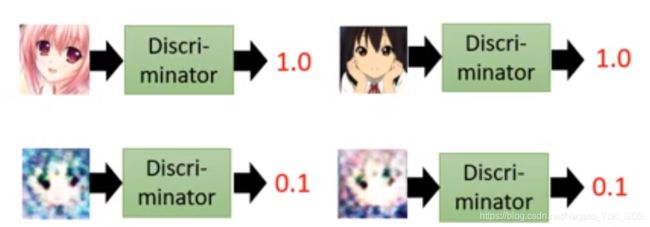
狭义的判别器就是输入数据(生成器产物或者真实数据),通过判别器,输出一个标量数值,输出的数值越大,则代表这个数据越真实。如下图示例(假设输出数值在0-1之间):
生成器和判别器的关系
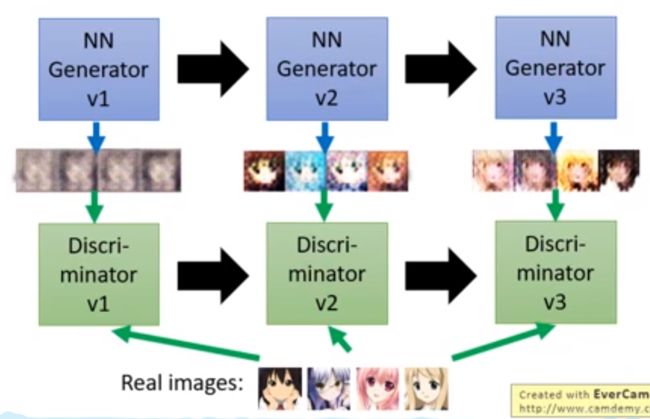
结合图来理解生成器和判别器的关系:
- 首先输入噪音让生成器v1生成图片
- 之后输入不同来源的图片到判别器v1,由判别器v1来判断图片是真实图片还是生成器生成的图片
- 然后为了骗过判别器,生成器v1升级为v2,再生成新的图片。
- 再将不同来源的图片输入到升级的判别器v2来判断图片是真实图片还是生成器生成的图片
- 依次循环下去,直到判别器无法区分图片来源,也就是生成器产生的图片真实度越来越接近真实图片的真实度。
GAN的训练流程简述
- 在每个训练迭代器中:
- 先训练判别器
- 从数万张图片(数据集)中采样出m个样本,即{ x 1 , x 2 , . . . , x m {x_1,x_2,...,x_m} x1,x2,...,xm}
- 随机从一个分布(高斯分布或均匀分布)里采样出有噪音的m个样本,即{ z 1 , z 2 , . . . , z m {z_1,z_2,...,z_m} z1,z2,...,zm}
- 通过生成器获得生成的数据,即{ x ‾ 1 , x ‾ 2 , . . . , x ‾ m {\overline x_1,\overline x_2,...,\overline x_m} x1,x2,...,xm},其中 x ‾ i \overline{x}_i xi=G( z i z_i zi)
- 更新判别器的参数使 v ‾ \overline v v最大。
- v ‾ = 1 m [ l o g D ( x i ) + l o g ( 1 − D ( x ‾ i ) ) ] \overline v=\frac{1}{m}[logD(x_i)+log(1-D(\overline x_i))] v=m1[logD(xi)+log(1−D(xi))]
- 梯度下降更新参数 θ d θ_d θd
- 再训练生成器
- 随机从一个分布(高斯分布或均匀分布)里采样出有噪音的m个样本,即{ z 1 , z 2 , . . . , z m {z_1,z_2,...,z_m} z1,z2,...,zm}
- 更新生成器的参数使 v ‾ \overline v v最小
- v ‾ = 1 m [ l o g D ( x i ) + l o g ( 1 − D ( x ‾ i ) ) ] \overline v=\frac{1}{m}[logD(x_i)+log(1-D(\overline x_i))] v=m1[logD(xi)+log(1−D(xi))]
- 梯度下降更新参数 θ g θ_g θg
- 先训练判别器
当训练判别器的时候,就相当于把生成器固定住了,当训练生成器的时候,就相当于把判别器固定住了,于是就有对上述关于 v ‾ \overline v v的讲解:
对于判别器,目标是提升辨认图片来源的能力,对真实图片输出大的数值,所以 D ( x i ) D(x_i) D(xi)越大越好, D ( x ‾ i ) D(\overline x_i) D(xi)越小越好,也就是 v ‾ \overline v v越大越好。
对于生成器:目的是希望自己生成的图片越来越真实,也就是要让 D ( x ‾ i ) D(\overline x_i) D(xi)越大越好,也就是 v ‾ \overline v v越小越好(另一项当成常数即可)。
论文中的生成模型和判别模型
GAN提出了两个模型:
-
生成模型(Generator)
生成模型主要是用来生成数据分布,目的是尽量与原数据分布接近。 -
判别模型(Discriminator)
判别模型主要是用来判断样本是来自真实分布还是生成模型生成的分布。目的是能够更加好地区分哪些样本来自真实数据,哪些样本来自生成模型的数据,越真实的数据得到的结果越大。
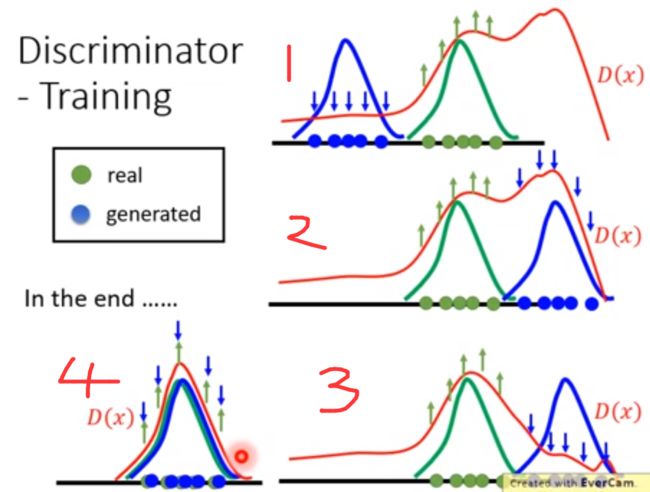
用数学来表示训练过程中两模型的变化,如下图:
绿色线表示真实数据的分布,蓝色线表示生成模型输出的数据分布,红色线表示判别器(越高就表示给的分数越大)
- 首先判别模型对真实数据的分布给高的分,对生成模型输出的数据分布给低分。
- 生成模型得出的分布就往分高的地方移动。
- 判别模型对生成模型得出的新分布进行打压,将它区域的分数压低。
- 不断执行2,3,最终生成模型输出数据的分布和真实数据的分布十分接近,判别器无法判断了。
GAN的数学理论
最大似然估计转换为最小化KL散度问题
真实数据的分布是 P d a t a ( x ) P_{data}(x) Pdata(x) ,我们定义一个分布 P G ( x i ; θ ) P_G(x_i;\theta) PG(xi;θ) ,我们想要找到一组参数 θ \theta θ,使得 P G ( x i ; θ ) P_G(x_i;\theta) PG(xi;θ)越接近 P d a t a ( x ) P_{data}(x) Pdata(x)越好。比如说, P G ( x i ; θ ) P_G(x_i;\theta) PG(xi;θ) 如果是一个高斯混合模型,那么 θ \theta θ就是均值和方差。
采用极大似然估计方法,我们从真实数据分布 P d a t a ( x ) P_{data}(x) Pdata(x)里面取样 m 个点, x 1 , x 2 , . . . , x m {x_1,x_2,...,x_m} x1,x2,...,xm,根据给定的参数 θ 我们可以算出某个x在该分布的概率 P G ( x i ; θ ) P_G(x_i;θ) PG(xi;θ),即:
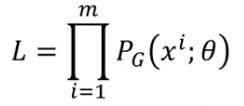
也可以将极大似然估计等价于最小化KL散度,我们需要找一个最大的 θ \theta θ使得 P G ( x i ; θ ) P_G(x_i;\theta) PG(xi;θ)接近 P d a t a ( x ) P_{data}(x) Pdata(x),就有下列式子:
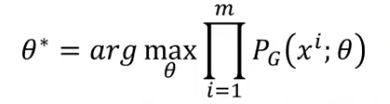
将其化简,得:
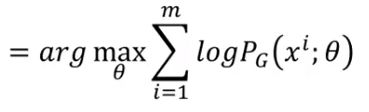
由于需要最大化概率的 θ \theta θ,也就是可以近似等价于原分布的期望,可得:
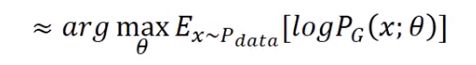
然后再展开成期望定义的形式,并且加减一项常数项(不含 θ \theta θ),不影响结果,有:
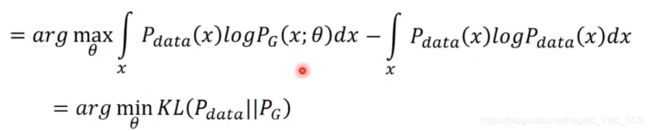
最终化成了最小化KL散度的形式。
其中KL散度用来衡量两种概率分布的相似程度,越小则表示两种概率分布越接近。形式为:
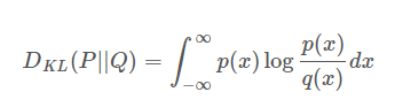
所以机器学习中的最大似然估计,其实就是最小化我们要寻找的目标分布 P G P_G PG与 P d a t a P_{data} Pdata的KL散度。
定义 P G P_G PG
如何来定义 P G P_G PG呢?
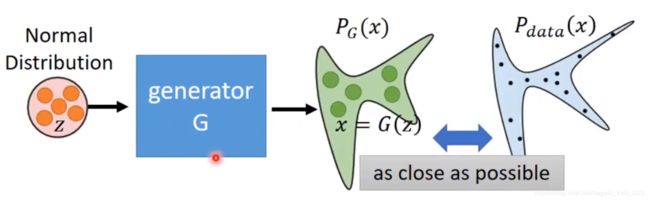
以前是采用高斯分布来定义的,但是生成的图片会很模糊,采用更复杂的分布的话,最大似然会没法计算。所以就引进了Generator来定义 P G P_G PG,如下图:
全局最优
优化目标是最小化 P G P_G PG与 P d a t a P_{data} Pdata之间的差异:
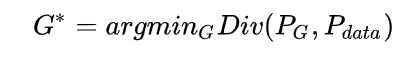
虽然我们不知道 P G P_G PG与 P d a t a P_{data} Pdata的公式,但是我们可以从这两个分布中采样出一些样本。
对 P G P_G PG,我们从给定的数据集中采样出一些样本。(该步骤对应训练判别器流程步骤1)
对 P d a t a P_{data} Pdata,我们随机采样出一些向量,经过Generator输出一些图片。(该步骤对应训练判别器流程步骤2,3)
之后经过Discriminator我们就可以计算 P G P_G PG与 P d a t a P_{data} Pdata的收敛。Discriminator的目标函数是:
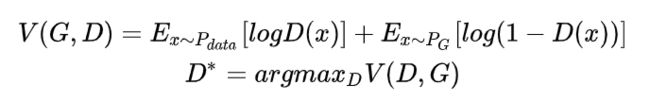
该目标函数对应训练判别器的损失函数,意思是假设x是从 P d a t a P_{data} Pdata 里面采样出来的,那么希望D(x)越大越好。如果是从 P G P_G PG里面采样出来的,就希望它的值越小越好。x~ P d a t a P_{data} Pdata表示该均值的x都来自 P d a t a P_{data} Pdata分布。
我们的目标是让判别器无法区分 P G P_G PG与 P d a t a P_{data} Pdata,也就是让它没办法把V(G,D)调大。接下来从数学上去解释这个结论。
给定生成器,我们要找到能最大化目标函数V(D,G)的D*:
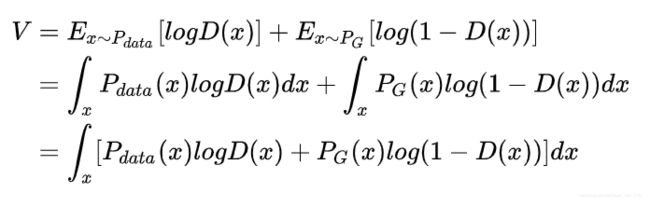
现在我们把积分里面的这一项拿出来看:
P d a t a l o g D ( x ) + P G ( x ) l o g ( 1 − D ( x ) ) P_{data}logD(x)+P_G(x)log(1-D(x)) PdatalogD(x)+PG(x)log(1−D(x))
我们想要找到一组参数D*,使这一项最大。把式子简写一下,将 P d a t a P_{data} Pdata用a表示, P G P_G PG用b表示,得:
f ( D ) = a l o g ( D ) + b l o g ( 1 − D ) f(D)=alog(D)+blog(1-D) f(D)=alog(D)+blog(1−D)
对D求导得:
d f ( D ) d D = a ∗ 1 D + b ∗ 1 1 − D ∗ ( − 1 ) \frac{df(D)}{dD}=a*\frac1D+b*\frac1{1-D}*(-1) dDdf(D)=a∗D1+b∗1−D1∗(−1)
另这个求导结果为0,得:
D ∗ = a a + b D^*=\frac a{a+b} D∗=a+ba
将a,b代回去,得:
D ∗ = P d a t a ( x ) P d a t a ( x ) + P G ( x ) D^*=\frac {P_{data}(x)}{P_{data}(x)+P_G(x)} D∗=Pdata(x)+PG(x)Pdata(x)
再将这个D带入V(G,D*)中,然后分子分母同时除以2,之后可以化简为JS散度形式(KL散度的变体,解决了KL散度非对称的问题),得:
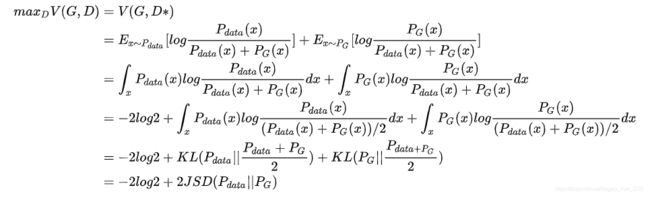
当 P d a t a P_{data} Pdata= P G P_G PG时,JS散度为0,值为-2log2,达到最优(也就是让判别器没办法把V(G,D)调大)。这是从正向证明当 P d a t a P_{data} Pdata= P G P_G PG时达到最优,还需从反向证明才可以得出当且仅当 P d a t a P_{data} Pdata= P G P_G PG才可以达到的全局最优。
反向证明很容易:假设 P d a t a P_{data} Pdata= P G P_G PG,那么D*= 1 2 \frac 12 21,再直接代入V(G,D*)即可得到-2log2。
所以,当且仅当 P d a t a P_{data} Pdata= P G P_G PG才可以达到的全局最优。也就是,当且仅当生成分布等于真实数据分布时,我们取得最优生成器。
我们从头整理一下,我们的目标是找到一个G*,去最小化 P d a t a P_{data} Pdata, P G P_G PG的差异,也就是:
G ∗ = a r g m i n G D i v ( P G , P d a t a ) G^*=argmin_GDiv(P_G,P_{data}) G∗=argminGDiv(PG,Pdata)
但是这个差异没法之间去算,所以就用一个判别器来计算这两个分布的差异:
D ∗ = a r g m a x D V ( D , G ) D^*=argmax_DV(D,G) D∗=argmaxDV(D,G)
所以优化目标就变为:
G ∗ = a r g m i n G m a x D V ( G , D ) G^*=argmin_Gmax_DV(G,D) G∗=argminGmaxDV(G,D)
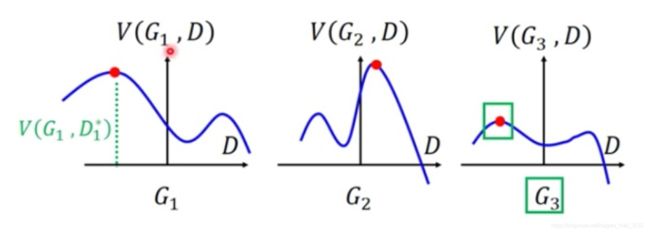
这个看起来很复杂,其实直观理解一下,如下图,我们假设已经把生成器固定住了,图片的曲线表示,红点表示固定住G后的 m a x D ( G , D ) max_D(G,D) maxD(G,D) , 也就是 P G P_G PG 和 P d a t a P_{data} Pdata 的差异。而我们的目标是最小化这个差异,所以下图的三个网络中, G 3 G_3 G3 是最优秀的。
参考的文章:
GAN论文阅读——原始GAN(基本概念及理论推导)
生成对抗网络(GAN) 背后的数学理论