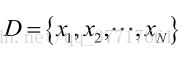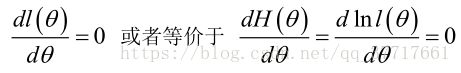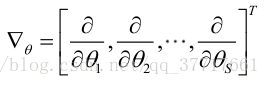生成对抗网络 GAN原理 学习笔记+实践

1. 生成模型与判别模型区别

判别模型： 直接求P(Y|X)
生成模型： 通过P(X,Y) / P(X) 求 P(Y|X) ，eg：隐马尔可夫链

2. 为什么要用生成模型？

1. 对高维数据和样本分布问题有很好的检测
2. 模拟强化学习(RL)
3. 数据缺失，半监督学习
4. 多模态(multy-modal)输出,eg：可能生出三只眼的狗，生成结果不好
5. 现实的生成任务，eg：给定一个groud truth的图片，将目标图片上面的马赛克去掉。
   
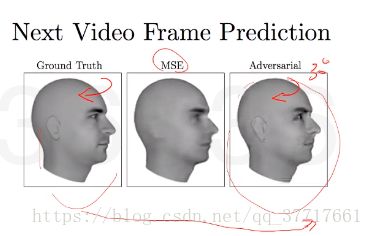
   eg：生成像素更高更清楚的图片
   
   eg: 图片到图片的翻译，完全是另外一个维度另外一个长相，生成所需求的图像。
   

3. 生成模型原理 —— 最大似然估计

通过最大似然估计，把整个数据分布给计算出来。
问题引出：
已知经典的贝叶斯公式

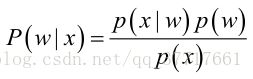
可惜现实生活中，先验概率或条件概率往往未知，所以要估计：

• 先验概率的估计较简单，1、每个样本所属的自然状态都是已知的（有监督学习）；2、依靠经验；3、用训练样本中各类出现的频率估计。

• 类条件概率的估计（非常难），原因包括：1、概率密度函数包含了一个随机变量的全部信息；2、样本数据可能不多；3、特征向量x的维度可能很大等等。总之要直接估计类条件概率的密度函数很难。解决的办法就是，把估计完全未知的概率密度转化为估计参数。 这里就将概率密度估计问题转化为参数估计问题，极大似然估计就是一种参数估计方法。

  所以得出估计的一个重要前提： 训练样本的分布能代表样本的真实分布。
  每个样本集中的样本都是所谓独立同分布的随机变量，且有充分的训练样本。
  

具体的步骤:

①独立采样, 可以只考虑一类样本集D，来估计参数向量θ。

② 似然(linkehood)估计：联合概率密度函数称为相对于
的θ的似然函数。

③求解极大似然函数
ML估计：求使得出现该组样本的概率最大的θ值。

实际中为了便于分析，定义了对数似然函数：

• 未知参数只有一个（θ为标量）

  在似然函数满足连续、可微的正则条件下，极大似然估计量是下面微分方程的解：

• 未知参数有多个（θ为向量）

  则θ可表示为具有S个分量的未知向量：

记梯度算子：

若似然函数满足连续可导的条件，则最大似然估计量就是如下方程的解。

     方程的解只是一个估计值，只有在样本数趋于无限多的时候，它才会接近于真实值。

引用：极大似然估计详解

4.生成模型大家族

5.生成对抗网络

1. 隐性code来控制数据的隐含关系
2. 数据会逐渐统一（不像变分方法）
3. 没有马尔科夫链的需要
4. 目前可以生成最好的样本 (因为目前没有好方法去评估模型)

生成G 与 判别D

D 为 Discriminator 判别器
G 为 Generator 生成器

• 判别器对假数据的损失原理相同，最终达到的目标是对于所有的真实图片，输出为1；对于所有的假图片，输出为0；
• 生成器的目标是从噪音输入(不带样本，且符合一定的分布)生成图片，愚弄判别器蒙混过关，需要达到的目标是对于生成的图片，输出为1(正好和鉴别器相反).

最终看重的是G的效果。

必要条件

z 是噪音输入（不带样本，且符合一定的分布），x是生成的样本

1. 必须可微
2. 没有可逆的需要(不需要能从x反推回z)
3. 可以训练任何size的z
4. 保证z的维度比x高

训练过程

简单理解与实验生成对抗网络GAN

• 同时在两个小批量数据（判别数据、生成数据）上使用SGD相关的方法(可以选择Adam)。
• 优化trick：可以让生成器(one player)训练得比判别器(the other player)学习得快一点。

三种生成损失函数

①

生成和真实差别越大，D的损失向负方向扩大，G的损失向正方向扩大。
②

1. D和G的损失函数不再绑定
2. G最大化使得D误判的对数概率
3. 可以先让D训练得不错，再让G加入战局

③ KL散度 （Kullback–Leibler divergence）

衡量两个分布的差距

假设 p 是真实分布，q是生成分布
左图，正KL(最大似然)：激进派，q拟合p，目的是把所有的分布都拟合进去，如果是双分布的话可能没办法拟合得好；
右图，逆 KL ：保守派，p拟合q，目的是能拟合好一个分布就算完成任务了。
eg：两个头的狗进行生成，用最大似然可能生成两倍大的头，用逆KL可能是生成只有一个头的狗，不会为了满足所有的分布，而更接近于真实。

应用场景

DCGAN (Deep Convolution GAN) : 一维数组映射到图片
大约等于 CNN 的逆过程

Keras实现代码

1. 导入库

    %matplotlib inline
    import os,random
    os.environ["KERAS_BACKEND"] = "tensorflow"
    import numpy as np
    import theano as th
    import theano.tensor as T
    from keras.utils import np_utils
    import keras.models as models
    from keras.layers import Input,merge
    from keras.layers.core import Reshape,Dense,Dropout,Activation,Flatten
    from keras.legacy.layers import MaxoutDense
    from keras.layers.advanced_activations import LeakyReLU
    from keras.activations import *
    from keras.layers.wrappers import TimeDistributed
    from keras.layers.noise import GaussianNoise
    from keras.layers.convolutional import Convolution2D, MaxPooling2D, ZeroPadding2D, Deconv2D, UpSampling2D
    from BatchNorm_GAN import BatchNormGAN
    from keras.layers.recurrent import LSTM
    from keras.regularizers import *
    from keras.layers.normalization import *
    from keras.optimizers import *
    from keras.datasets import mnist
    import matplotlib.pyplot as plt
    import pickle, random, sys, keras
    from keras.models import Model
    from IPython import display
    
    sys.path.append("../common")
    from keras.utils import np_utils
    from tqdm import tqdm
    
    K.set_image_dim_ordering('th')
   

2. 准备训练集

    #28 x 28 的图片
    img_rows, img_cols = 28, 28
    
    #把数据集洗一洗
    (X_train, y_train), (X_test, y_test) = mnist.load_data()
    
    #排好
    X_train = X_train.reshape(X_train.shape[0], 1, img_rows, img_cols)
    X_test = X_test.reshape(X_test.shape[0], 1, img_rows, img_cols)
    X_train = X_train.astype('float32')
    X_test = X_test.astype('float32')
    X_train /= 255
    X_test /= 255
    
    #看看我们所有数据的个数和长相
    print(np.min(X_train), np.max(X_train))
    print('X_train shape:', X_train.shape)
    print(X_train.shape[0], 'train samples')
    print(X_test.shape[0], 'test samples')
   

输出

3. 做个指示器，告诉算法，现在这个net（要么是dis要么是gen），能不能被继续train

    def make_trainable(net, val):
        net.trainable = val
        for l in net.layers:
            l.trainable = val
   

4. 搭建网络结构

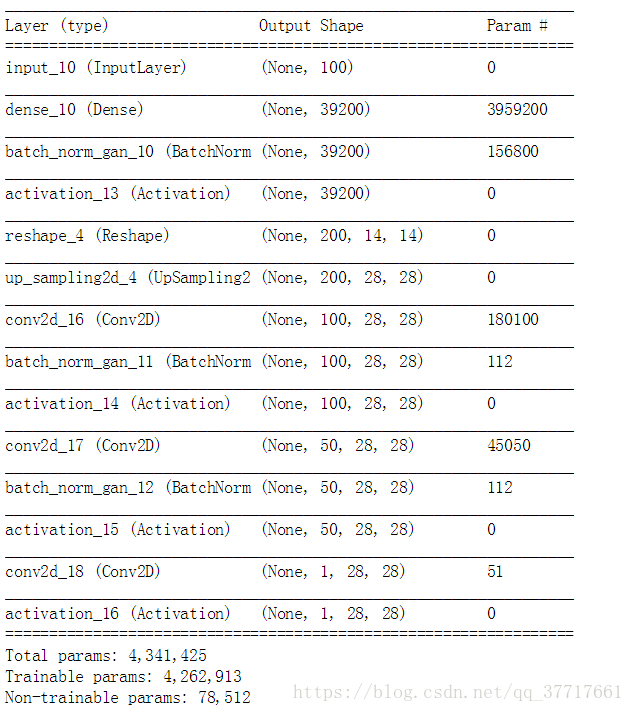
   # 看一个每一个训练数据的长相
    shp = X_train.shape[1:]
    print(shp)
    dropout_rate = 0.25
    
    # 设置gen和dis的opt
    # 大家可以尝试各种组合
    opt = Adam(lr=1e-3)
    dopt = Adam(lr=1e-4)
    #opt = Adam(lr=1e-3)
    #opt = Adamax(lr=1e-4)
    #opt = Adam(lr=0.0002)
    #opt = Adam(lr=0.0002, beta_1=0.5, beta_2=0.999, epsilon=1e-08)
    nch = 200
    
    # 造个GEN
    nch = 200
    g_input = Input(shape=[100])
    # 倒过来的CNN第一层（也就是普通CNN那个flatten那一层）
    H = Dense(nch*14*14, init='glorot_normal')(g_input)
    H = BatchNormGAN()(H)
    H = Activation('relu')(H)
    H = Reshape( [nch, 14, 14] )(H) 
    # upscale上去2倍大。也就是从14x14 到 28x28
    H = UpSampling2D(size=(2, 2))(H)
    # CNN滤镜
    H = Convolution2D(int(nch/2), 3, 3, border_mode='same', init='glorot_uniform')(H)
    H = BatchNormGAN()(H)
    H = Activation('relu')(H)
    # CNN滤镜
    H = Convolution2D(int(nch/4), 3, 3, border_mode='same', init='glorot_uniform')(H)
    H = BatchNormGAN()(H)
    H = Activation('relu')(H)
    # 合成一个大图片
    H = Convolution2D(1, 1, 1, border_mode='same', init='glorot_uniform')(H)
    g_V = Activation('sigmoid')(H)
    generator = Model(g_input,g_V)
    generator.compile(loss='binary_crossentropy', optimizer=opt)
    generator.summary()
   

输出

	# 造个DIS
	# 这就是一个正常的CNN
	d_input = Input(shape=shp)
	# 滤镜
	H = Convolution2D(256, 5, 5, subsample=(2, 2), border_mode = 'same', activation='relu')(d_input)
	H = LeakyReLU(0.2)(H)
	H = Dropout(dropout_rate)(H)
	# 滤镜
	H = Convolution2D(512, 5, 5, subsample=(2, 2), border_mode = 'same', activation='relu')(H)
	H = LeakyReLU(0.2)(H)
	H = Dropout(dropout_rate)(H)
	H = Flatten()(H)
	# flatten之后，接MLP
	H = Dense(256)(H)
	H = LeakyReLU(0.2)(H)
	H = Dropout(dropout_rate)(H)
	# 出一个结果，『是』或者『不是』
	d_V = Dense(2,activation='softmax')(H)
	discriminator = Model(d_input,d_V)
	discriminator.compile(loss='categorical_crossentropy', optimizer=dopt)
	discriminator.summary()

输出

	make_trainable(discriminator, False)
	# 为stacked GAN做准备
	# 然后合成一个GAN的构架
	gan_input = Input(shape=[100])
	H = generator(gan_input)
	gan_V = discriminator(H)
	GAN = Model(gan_input, gan_V)
	
	GAN.compile(loss='categorical_crossentropy', optimizer=opt)
	GAN.summary()

输出

5. 两个画图功能

    def plot_loss(losses):
            display.clear_output(wait=True)
            display.display(plt.gcf())
            plt.figure(figsize=(10,8))
            plt.plot(losses["d"], label='discriminitive loss')
            plt.plot(losses["g"], label='generative loss')
            plt.legend()
            plt.show()
    def plot_gen(n_ex=16,dim=(4,4), figsize=(10,10) ):
        noise = np.random.uniform(0,1,size=[n_ex,100])
        generated_images = generator.predict(noise)
    
        plt.figure(figsize=figsize)
        for i in range(generated_images.shape[0]):
            plt.subplot(dim[0],dim[1],i+1)
            img = generated_images[i,0,:,:]
            plt.imshow(img)
            plt.axis('off')
        plt.tight_layout()
        plt.show()
   

6. 正式训练

    # 设置一下存储D和G的格式
    losses = {"d":[], "g":[]}
    # 训练正经去了
    def train_for_n(nb_epoch=5000, plt_frq=25,BATCH_SIZE=32):
        for e in tqdm(range(nb_epoch)):  
            
            # 生成图片
            image_batch = X_train[np.random.randint(0,X_train.shape[0],size=BATCH_SIZE),:,:,:]    
            noise_gen = np.random.uniform(0,1,size=[BATCH_SIZE,100])
            generated_images = generator.predict(noise_gen)
            
            # 训练DIS
            X = np.concatenate((image_batch, generated_images))
            y = np.zeros([2*BATCH_SIZE,2])
            y[0:BATCH_SIZE,1] = 1
            y[BATCH_SIZE:,0] = 1
            # 当然，要让DIS可以被训练
            make_trainable(discriminator,True)
            d_loss  = discriminator.train_on_batch(X,y)   #返回loss的标量值或list
            
            losses["d"].append(d_loss)
        
            # 训练 Generator-Discriminator stack
            noise_tr = np.random.uniform(0,1,size=[BATCH_SIZE,100])
            y2 = np.zeros([BATCH_SIZE,2])
            y2[:,1] = 1
            # 这个时候，让DIS不能被变化。保证判断结果一致性
            make_trainable(discriminator,False)
            g_loss = GAN.train_on_batch(noise_tr, y2 )
            losses["g"].append(g_loss)
            
            # 看看新图长什么样子
            if e%plt_frq==plt_frq-1:
                plot_loss(losses)
                plot_gen()
               
   
    train_for_n(nb_epoch=250, plt_frq=25,BATCH_SIZE=128)
   

   输出