理解:用变分推断统一理解深度生成模型(VAE、GAN、AAE、ALI(BiGAN))
参考文章:https://kexue.fm/archives/5716
https://zhuanlan.zhihu.com/p/40282714
本篇博客主要是参照上述两个博文,另外加入了一些自己的理解,也为了和自己学习或者常见的知识做一个对照,因为在学习过程中总有一个问题困扰,就是符号,前后的符号对照不好,还得想半天。所以有些符合可能跟原文章对不上,但跟我之前的博客可以对上。
特意将常用的符号归纳一下(当然我也是希望和我之前的博客的符号相一致,但是可惜还是没能做好):
![]() →真实数据的分布,或者称为x的证据分布(在《模式分类(第二版)》中贝叶斯决策这一章里这样描述)
→真实数据的分布,或者称为x的证据分布(在《模式分类(第二版)》中贝叶斯决策这一章里这样描述)![]() →隐变量(VAE)或噪声数据(GAN)
→隐变量(VAE)或噪声数据(GAN)![]() 或
或![]() 或
或![]() →生成模型的分布这些符号的记法不同,只是为了方便不同的推导和作者们不同的理解角度,最主要的我们在生成模型中要研究的就是找到一个合适的参数
→生成模型的分布这些符号的记法不同,只是为了方便不同的推导和作者们不同的理解角度,最主要的我们在生成模型中要研究的就是找到一个合适的参数![]() 使得
使得![]() 近似于
近似于![]() 。
。
对于GAN,我们现有的认识角度至少包括以下几个:
- minmax博弈。GAN提出时也是从这个角度阐述的。生成对抗网络中“对抗”一词也从这儿来的。
- 最优传输理论。参见这里,WGAN的生成器计算最优传输映射,判别器计算Wasserstein距离。
- 变分推断。这是新的视角,参见用变分推断统一理解生成模型、Variational Inference: A Unified Framework of Generative Models and Some Revelations。这也是这篇博客所要说明的一点,为什么题目称为理解,原因就是在推导文中公式的过程中出现了一些难点,所以列举在此。
1、变分推断新解
假设![]() 是显变量(或者我们称之为样本),
是显变量(或者我们称之为样本),![]() 为隐变量(或者我们称之为噪音数据)。
为隐变量(或者我们称之为噪音数据)。![]() 为
为![]() 的证据分布,或者成为真实数据的分布,并且有
的证据分布,或者成为真实数据的分布,并且有
生成模型要求的就是希望找到一个最优的参数![]() 使得
使得![]() 能逼近
能逼近![]() ,所以一般情况下,我们会最大化似然函数:
,所以一般情况下,我们会最大化似然函数:
![]() ……(2)
……(2)
原文中将![]() 省去,可以认为默认
省去,可以认为默认![]() 是带有参数
是带有参数![]() 的,为了简单起见,我们这里也就不带有参数
的,为了简单起见,我们这里也就不带有参数![]() 。
。
最大化(2)式的似然函数等价于最小化KL散度![]() ,这个我在机器学习与信息论之熵那篇博客中就提到过,这里似然函数可以看做交叉熵,而KL散度(也就是相对熵)与交叉熵之间是有关系的:
,这个我在机器学习与信息论之熵那篇博客中就提到过,这里似然函数可以看做交叉熵,而KL散度(也就是相对熵)与交叉熵之间是有关系的:
等式的前一部分恰巧就是p的熵,等式的后一部分,就是交叉熵:由于KL散度中的前一部分![]() 不变,所以最大化交叉熵和最小化KL散度是等价的。
不变,所以最大化交叉熵和最小化KL散度是等价的。
这里我们转化为最小化KL散度![]() :
:
但是由于积分难以计算,因此大多数情况下都难以直接优化。
变分推断中,首先引入联合分布![]() 使得
使得![]() ,而变分推断的本质,就是将边缘分布的KL散度
,而变分推断的本质,就是将边缘分布的KL散度![]() 改为联合分布的KL散度
改为联合分布的KL散度![]() ,而
,而
……(4)
(4)式表明联合分布的KL散度是边缘分布的KL散度的一个更强的条件上界。所以一旦优化成功,也就是KL散度最小(或者两个联合分布的距离很小),那么我们就得到![]() ,从而
,从而![]() ,即
,即![]() 成为了真实数据分布
成为了真实数据分布![]() 的一个近似。
的一个近似。
当然,引入变分推断也不是加强条件而加强,而是因为在很多情况下,![]() 比
比![]() gen更容易计算。所以变分推断是提供了一个可计算的方案。
gen更容易计算。所以变分推断是提供了一个可计算的方案。
2、VAE和EM算法
结合上述关于变分推断的新理解,我们可以简单导出两个基本的算法就是:变分自动编码器和EM算法。
2.1 VAE
在VAE中,假设![]() ,
,![]() ,其中
,其中![]() 是带有未知参数的高斯分布(代表解码器或生成器),
是带有未知参数的高斯分布(代表解码器或生成器),![]() 是带有未知参数的高斯分布(代表编码器),
是带有未知参数的高斯分布(代表编码器),![]() 是标准的高斯分布(代表我们想要生成的编码符合高斯分布)。从联合概率分布或上述变分推断的角度考虑,最小化的目标函数是:
是标准的高斯分布(代表我们想要生成的编码符合高斯分布)。从联合概率分布或上述变分推断的角度考虑,最小化的目标函数是:
(5)式中![]() 不包含优化目标,可以看做常数,而对
不包含优化目标,可以看做常数,而对![]() 的积分可以转化为对样本的采样,(5)式可转化为:
的积分可以转化为对样本的采样,(5)式可转化为:
![]() ……(6)
……(6)
因为在VAE中![]() 、
、![]() 都是带有参数的神经网络(高斯分布),这时候
都是带有参数的神经网络(高斯分布),这时候![]() 可以显示的算出也就是我们常见的VAE的损失函数中的正则化项。并且通过重参数技巧来采样一个点完成积分
可以显示的算出也就是我们常见的VAE的损失函数中的正则化项。并且通过重参数技巧来采样一个点完成积分![]() 的估算,可以得到VAE最终要最小化的loss:
的估算,可以得到VAE最终要最小化的loss:
![]() ……(7)
……(7)
这一部分的推导很简单,再有不明白的可以参看原作者的文章:变分自编码器
2.2 EM算法
很明显,在VAE中我们对后验分布做了约束,仅假设它是高斯分布(VAE的原始论文也提到了其他的分布,但是效果可能都没这么好),所以我们优化的是高斯分布的参数,如果不作此假设,那么直接优化原始目标(5)式,在某种情况下也是可操作的,但这个时候只能采用交替优化的方式,先固定![]() ,优化
,优化![]() ,那么就有
,那么就有
注意:(5)式我们需要最小化,我们对(8)做的是最大化的过程。(8)式相当于我们的常见EM算法的M步,优化![]() 模型中的参数。
模型中的参数。
完成这一步后,我们固定![]() ,优化
,优化![]() ,再此之前先将
,再此之前先将![]() 写成
写成![]() 的形式:
的形式:
那么有:
……(10)
由于现在对![]() 没有约束,因此可以直接让
没有约束,因此可以直接让![]() 使得loss等于0。也就是说,
使得loss等于0。也就是说,![]() 有理论最优解:
有理论最优解:
最优化![]() ,相当于我们常见EM算法的E步。
,相当于我们常见EM算法的E步。
这里的(8)和(11)交替执行,构成了EM算法的求解步骤。这样,我们从变分推断框架下快速的得到了EM算法。
3、变分推断下的GAN
在这部分内容,将一般的GAN纳入变分推断中,这将为我们进一步认识GAN打开新的思路。并且作者还通过推导得到了一个有效的正则化项,引出了VGAN。
3.1 变分推断看GAN
同VAE一样,GAN也希望能训练一个生成模型![]() ,来将
,来将![]() 映射为数据分布
映射为数据分布![]() ,不同于VAE中将
,不同于VAE中将![]() 选择为高斯分布,GAN的选择是:
选择为高斯分布,GAN的选择是:
![]() ……(12)
……(12)
其中,![]() 是狄拉克函数,狄拉克函数除了零点以外取值都为0。这种单点分布可以看做方差无限小的高斯分布。
是狄拉克函数,狄拉克函数除了零点以外取值都为0。这种单点分布可以看做方差无限小的高斯分布。![]() 就是生成器的神经网络。
就是生成器的神经网络。
注:VAE选择高斯分布,会带来模糊,而GAN选择的是狄拉克函数,它只在单点有响应,如果能够优化,则真假样本必然需要充分接近,生成的样本就是sharp(聪明)的。
简单理解GAN比VAE生成的样本更好?
主要区别在于VAE和GAN的目标函数不同,GAN的目标函数要么是似然要么是分布相似性的度量,两者都是衡量生成样本的分布质量的重要指标。而VAE(AE)的目标是重构误差,也就是它不管分布如何,只需要能够比较好的压缩并重构样本即可。
一般我们认为![]() 是隐变量,但由于狄拉克函数实际上是单点分布,因此可以认为
是隐变量,但由于狄拉克函数实际上是单点分布,因此可以认为![]() 与
与![]() 的关系已经是一一对应的,所以
的关系已经是一一对应的,所以![]() 与
与![]() 的关系已经不够“随机”了,在GAN中我们认为它不是隐变量(意味着我们不需要考虑后验分布
的关系已经不够“随机”了,在GAN中我们认为它不是隐变量(意味着我们不需要考虑后验分布![]() )。
)。
事实上,在GAN中仅仅引入一个二元的隐变量![]() 来构成联合分布,也就是现在我们需要构造一个分类问题,分真假样本,则有联合分布(也就是我们对于来自于真实数据的样本分类为1,对于来自于生成数据的样本分类为0):
来构成联合分布,也就是现在我们需要构造一个分类问题,分真假样本,则有联合分布(也就是我们对于来自于真实数据的样本分类为1,对于来自于生成数据的样本分类为0):
这里![]() 描述了一个二元概率分布,我们直接取
描述了一个二元概率分布,我们直接取![]() 。另一方面,我们设
。另一方面,我们设![]() ,
,![]() 是一个条件伯努利分布。而优化目标是另一个方向的
是一个条件伯努利分布。而优化目标是另一个方向的![]() (这也很容易理解,我们想让我们的生成分布区逼近真实数据的分布)。
(这也很容易理解,我们想让我们的生成分布区逼近真实数据的分布)。
……(14)
一旦优化成功,那么就有![]() ,那么就有
,那么就有
从而![]() ,完成了生成模型的构建。
,完成了生成模型的构建。
现在我们优化对象有![]() 和
和![]() ,记
,记![]() ,也就是说,判别器输出样本属于真样本的概率。才有交替更新的方法求解。先固定
,也就是说,判别器输出样本属于真样本的概率。才有交替更新的方法求解。先固定![]() ,即固定
,即固定![]() ,也就意味着
,也就意味着![]() 也固定了,然后优化
也固定了,然后优化![]() ,即求解D:
,即求解D:
![]() ……(16)
……(16)
这也就是我们的零和博弈的GAN(原始的GAN)关于D优化的目标函数。
如果保留![]() ,则:
,则:
![]()
也就是说, ![]() 控制着真假样本的权重。
控制着真假样本的权重。
然后固定![]() (也就是
(也就是![]() 固定),优化
固定),优化![]() ,这时相关的loss就为:
,这时相关的loss就为:
这里包含我们不知道的![]() ,但是假如
,但是假如![]() 模型具有足够的拟合能力,那么跟(11)式同理,
模型具有足够的拟合能力,那么跟(11)式同理,![]() 应该有最优解,最优解为(原始的GAN论文中关于这个最优解有证明,可以见我上一篇博客):
应该有最优解,最优解为(原始的GAN论文中关于这个最优解有证明,可以见我上一篇博客):
![]() ……(18)
……(18)
其中, ![]() 是前一阶段的
是前一阶段的 ![]() ,简单看成是来自于上次迭代的即可。将
,简单看成是来自于上次迭代的即可。将 ![]() 的最优解代入
的最优解代入 ![]() 的目标函数,化简得到:
的目标函数,化简得到:
该目标和原始的GAN相差一个KL项。
3.2 变分推断下生成器的目标
可以看到,(19)式的第一项就是标准GAN生成器所采用的loss:
![]() ……(20)
……(20)
而通过变分推断推导多出了的第二项,可以将其描述为新分布与旧分布之间的距离。这两项loss是对抗的。因为![]() 希望新旧分布尽量一致,但是如果判别器充分优化的话,对于旧分布
希望新旧分布尽量一致,但是如果判别器充分优化的话,对于旧分布![]() 中的样本,
中的样本,![]() 都很小(几乎被认为就是负样本),所以
都很小(几乎被认为就是负样本),所以![]() 会相当大,反之亦然。这样一来,整个loss一起优化的话,模型既要“传承”旧分布
会相当大,反之亦然。这样一来,整个loss一起优化的话,模型既要“传承”旧分布![]() ,同时要在新方向
,同时要在新方向![]() 探索,在新旧之间插值。
探索,在新旧之间插值。
我们知道,目前标准的GAN的生成器loss都不包含![]() ,这事实上造成了loss的不完备。假设有一个优化算法总能找到G(z)的理论最优解、并且G(z)具有无限的拟合能力,那么G(z)只需要生成唯一一个使得D(x)最大的样本(不管输入的z是什么),这就是模型坍缩。这样说的话,理论上它一定会发生。
,这事实上造成了loss的不完备。假设有一个优化算法总能找到G(z)的理论最优解、并且G(z)具有无限的拟合能力,那么G(z)只需要生成唯一一个使得D(x)最大的样本(不管输入的z是什么),这就是模型坍缩。这样说的话,理论上它一定会发生。
那么,![]() 给我们什么启发呢?我们设
给我们什么启发呢?我们设
![]() ……(21)
……(21)
其中 ![]() 为生成器的参数改变量,对
为生成器的参数改变量,对 ![]() 做估计。首先对
做估计。首先对 ![]() 做泰勒展开
做泰勒展开
于是:
其中第三行利用了 ,第四行第一项假设求导跟积分可交换,最后一行做了可积的假设。
上述的粗略估计表明,生成器不能迈太大步子。稳健才是正道。
这一部分的分析,只适用于生成器,判别器本身不受约束。
3.3 估算生成器的正则项
与之前引入变分推断一样,直接计算![]() 难以计算和估计,但是可以通过
难以计算和估计,但是可以通过 ![]() 来估计:
来估计:
![]() ……(23)
……(23)
将狄拉克分布看成高斯分布在方差趋于0时的极限,即
将(24)式带入(23)式可得:
因此完整的生成器的loss可以选为:
也就是说,可以用新旧生成样本的距离作为正则项,正则项保证模型不会过于偏离旧分布。
4、GAN的其他变式
对抗自编码器(Adversarial Autoencoders,AAE)和对抗推断学习(Adversarially Learned Inference,ALI)这两个模型是GAN的变种之一,也可以被纳入到变分推断中。
4.1 变分推断下的AAE
事实上,只需要在GAN的论述中,将![]() 的位置交换,就得到了AAE的框架。
的位置交换,就得到了AAE的框架。
(图采自原始论文,但图中的符号和这里推导的符号正好相反)
具体来说,AAE希望能够训练一个编码模型![]() ,来将真实分布
,来将真实分布![]() 映射成标准高斯分布
映射成标准高斯分布![]() ,而:
,而:
![]() ……(27)
……(27)
其中![]() 就是编码器的神经网络。
就是编码器的神经网络。
同GAN一样,AAE引入了一个二元的隐变量y,用来构造真假分类问题,则有:
同样直接取![]() 。另一方面,我们设
。另一方面,我们设![]() ,这里的后验分布
,这里的后验分布![]() 是一个输入为
是一个输入为![]() 的二元分布可以理解为判别模型,然后去优化
的二元分布可以理解为判别模型,然后去优化![]() (因为
(因为![]() 是已知分布):
是已知分布):
……(29)
现在我们的优化对象就有![]() 和
和![]() ,记
,记![]() (因为这里想让来自于q分布的得分更好),依然进行交替迭代:先固定
(因为这里想让来自于q分布的得分更好),依然进行交替迭代:先固定![]() ,这也就意味着
,这也就意味着![]() 就固定了,然后优化
就固定了,然后优化![]() ,得到优化目标:
,得到优化目标:
![]() ……(30)
……(30)
然后固定![]() 来优化
来优化![]() ,这时候相关的loss为:
,这时候相关的loss为:
利用![]() 的理论最优解:
的理论最优解:
将其带入(31)式中,可得:
一方面,同标准的GAN一样,我们可以去掉第二项,得到:
![]() ……(33)
……(33)
另一方面,我们可以得到编码器之后在训练一个解码器![]() ,但是如果所假设的
,但是如果所假设的![]() 的拟合能力是充分的,重构误差可以足够小,那么将
的拟合能力是充分的,重构误差可以足够小,那么将![]() 加入到上述loss中并不会干扰对抗部分的训练,因此可以联合训练:
加入到上述loss中并不会干扰对抗部分的训练,因此可以联合训练:
![]() ……(33)
……(33)
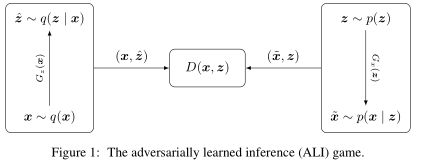
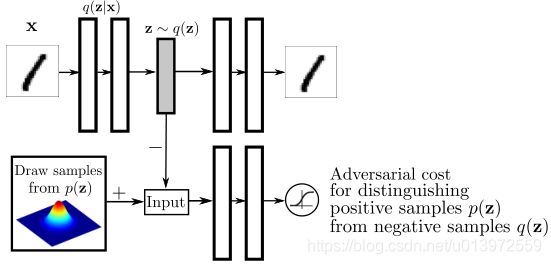
4.2 变分推断下的ALI
(图采自原始论文,但图中的符号和这里推导的符号正好相反)
ALI像是GAN和AAE的融合,另一个几乎一样的工作是BiGAN。相比于GAN,它将![]() 也作为隐变量纳入到变分推断中。具体来说还是构造一个二分类问题,引入新的变量
也作为隐变量纳入到变分推断中。具体来说还是构造一个二分类问题,引入新的变量![]() ,ALI中有:
,ALI中有:
以及![]() ,然后去优化
,然后去优化![]() :
:
等价于最小化:
现在优化的对象有![]() ,记
,记![]() ,而
,而![]() 是一个带有编码器
是一个带有编码器![]() 的高斯分布或狄拉克分布,
的高斯分布或狄拉克分布,![]() 是一个带有生成器
是一个带有生成器![]() 的高斯分布或狄拉克分布。依旧交替优化:先固定
的高斯分布或狄拉克分布。依旧交替优化:先固定![]() ,那么与
,那么与![]() 相关的loss为:
相关的loss为:
![]() ……(38)
……(38)
跟VAE一样,对![]() 和
和![]() 的期望可以通过重参数技巧完成。接着固定
的期望可以通过重参数技巧完成。接着固定![]() 来优化
来优化![]() ,因为这时候有
,因为这时候有![]() 又有
又有![]() ,整个loss不能简化,还是类似于(37)那样,但利用
,整个loss不能简化,还是类似于(37)那样,但利用![]() 的最优解:
的最优解:
可以转化为:
由于![]() 、
、![]() 都是高斯分布,事实上后两项我们可以具体地算出来(配合重参数技巧),但同标准GAN一样,为了谨慎的训练,我们可以简单去掉后面两项,得到:
都是高斯分布,事实上后两项我们可以具体地算出来(配合重参数技巧),但同标准GAN一样,为了谨慎的训练,我们可以简单去掉后面两项,得到:
这就是我们通过变分推断导出的ALI的生成器和编码器的loss,它跟标准的ALI结构有所不同。标准的ALI(包括普通的GAN)将其视为一个极大极小问题,所以编码器和生成器的loss为:
或:
无论(42)还是(43)都与我们推出来的(41)不同,这说明,将对抗网络视为一个极大极小问题仅是一个直觉行为,并非总是应该如此。
当然,本博文所有的内容主要是参考苏剑林的博客,如果理解上有误差欢迎大家一起学习交流。
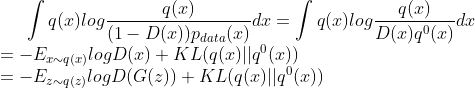
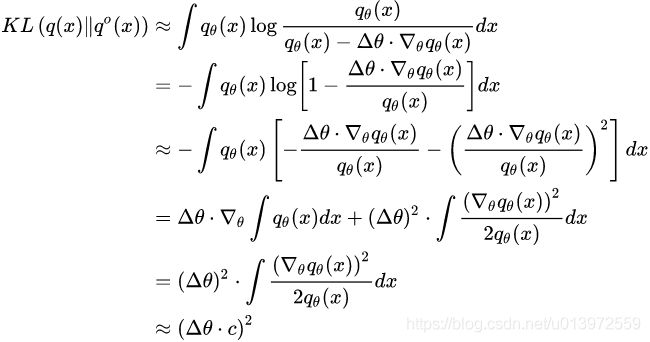
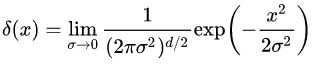
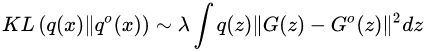
![\int p(z)log\frac{p(z)}{(1-D(z))q(z)}dz=\int p(z)log\frac{p(z)}{D(z)p^{0}(z)}dz\\ =E_{x\sim p_{data}(x)}[-log D(E(x))]+KL(p(z)||p^{0}(z))](http://img.e-com-net.com/image/info8/0fbe7711e21343c1b34a4d463f78ee6a.gif)