【笔记】对称密码之分组密码的工作模式

一、前言

分组密码不仅仅是一个加密算法，也是用于实现多种不同密码学编制机制的万能元件。本文先介绍分组密码的设计原则，再介绍五种主要的分组工作模式，包括了它们的流程、特点以及攻击方法，最后列出几道CTF中的相关赛题。

二、分组密码概述

在今天我们所使用的加密法中，分组加密是最常见的类型。分组加密法每次作用于固定大小的分组（与流密码不同，流密码每次加密数据流的一位或一个字节），一个分组的比特数就称为分组长度，典型的分组大小是64位或128位。与流密码一样， 两个用户要共享一个对称加密密钥。使用某些工作模式，分组密码可以获得与流密码相同的效果。一般来说，分组密码的应用范围比流密码要广泛，且绝大部分基于网络的对称密码应用使用的是分组密码。

分组密码是许多系统安全的一个重要组成部分。可用于构造：

• 伪随机数生成器
• 流密码
• 消息认证码(MAC)和杂凑函数
• 消息认证技术、数据完整性机制、实体认证协议以及单钥数字签字体制的核心组成部分。

分组密码实质上是字长为$n$的数字序列的代换密码，如下图所示：

2.1分组密码的设计原则

分组密码的设计问题在于找到一种算法，能在密钥控制下从一个足够大且足够好的置换子集中，简单而迅速地选出一个置换，用来对当前输入的明文的数字组进行加密变换。

分组密码算法应满足的要求:

• 分组长度n要足够大：防止明文穷举攻击
• 密钥量要足够大：尽可能消除弱密钥并使所有密钥同等地好，防止密钥穷举攻击
• 由密钥确定置换的算法要足够复杂: 充分实现明文与密钥的扩散和混淆，没有简单的关系可循，要能抗击各种已知的攻击
• 加密和解密运算简单：易于软件和硬件高速实现
• 数据扩展：一般无数据扩展，在采用同态置换和随机化加密技术时可引入数据扩展
• 差错传播尽可能地小：一个密文分组的错误尽可能少的影响其他密文分组的解密

2.2混淆和扩散

混淆和扩散是由Shannon提出的设计密码系统的两个基本方法，目的是抗击攻击者对密码系统的统计分析。

混淆原则(Confusion)：

• 混淆原则就是将密文、明文、密钥三者之间的统计关系和代数关系变得尽可能复杂，使得敌手即使获得了密文和明文，也无法求出密钥的任何信息；即使获得了密文和明文的统计规律，也无法求出明文的新的信息。
• 可进一步理解为：明文不能由已知的明文，密文及少许密钥比特代数地或统计地表 示出来； 密钥不能由已知的明文，密文及少许密钥比特代数地或统计地表示出来。

扩散原则(Diffusion)：

• 扩散原则就是应将明文的统计规律和结构规律散射到相当长的一段统计中去(Shannon的原话)。 也就是说让明文中的每一位影响密文中的尽可能多的位，或者说让密文中的每一位都受到明文中的尽可能多位的影响。
• 如果当明文变化一个比特时，密文有某些比特不可能发生变化，则这个明文就与那些密文无关，因而在攻击这个明文比比特时就可不利用那些密文比。

三、分组加密法的模式

为什么需要工作模式：

• 分组密码的工作模式是：根据不同的数据格式和安全性要求，以一个具体的分组密码算法为基础构造一个分组密码系统的方法
• 分组密码的工作模式应当力求简单，有效和易于实现
• 需要采用适当的工作模式来隐蔽明，文的统计特性、数据的格式等
• 降低删除、重放、插入和伪造成功的机会

3.1电码本ECB（Electronic Code Book）模式

电码本(ECB)模式一次处理一组明文分块，每次使用相同的密钥加密。使用电码本这个词是因为对于给定的密钥，任何b位的明文组只有唯一密文与之对应，所以可以想象存在一个很厚的密码本，根据任意b位明文都可以查到相应的密文。

明文若长于b位，则可简单将其分成b位一-组的块，有必要则可对最后一块进行填充。解密也是一-执行一块，且使用相同的密钥。明文(必要的时候进行填充)由一串b位的块组成，记为P, P₂, … P_v，相应的密文分组依次是C，C₂, … C_N。我们可以如下定义ECB 模式。

特点和不足:

• 简单有效，易于标准化
• 可以并行处理
• 不存在误差传递问题
• 会泄露明文模式相同的明文会加密成相同的密文，通过密文可能会泄露明文的加密模式

对ECB模式的攻击：

每个明文分组都是各自独立地进行加密和解密，但这其实是一个很大的弱点。假如存在一个攻击者，当他作为中间人截获两方的通信时，他能够改变密文的分组顺序，当接收者对密文进行解密时，由于密文分组的顺序被改变了，因此相应的明文分组的顺序也被改变了，那么接收者实际上是解密出了一段被篡改后的密文。

例：假设银行A和银行B之间的资金转帐系统所使用报文模式如下:

敌手C通过截收从A到B的加密消息，只要将第5至第12分组替换为自己的姓名和帐号相对应的密文，即可将别人的存款存入自己的帐号。

3.2密码分组链接CBC（Cipher Block Chaining）模式

为了克服ECB的弱点，我们需要将重复的明文分组加密成不同的密文分组。满足这一要求的简单方法是使用CBC模式。这种模式下加密算法的输人是当前的明文组和
上一个密文组的异或，而使用的密钥是相同的，相当于将所有的明文组链接起来。

加解密方式:

• 加密: $C_i=E_K(C_i-1$ $⨁$ $P_i)$
• 解密: $P_i=D_K$

第一块明文可以和一个初始向量($IV$)异或后再加密，以产生第一一个明文分组。解密时将第一块密文解密的结果与$IV$异或而恢复出第一块明文。$IV$是和密文具有相同长度的数据分组。

特点和不足：

• 引入随机的初始向量，安全性好于ECB
• 适合于传输多个分组
• 是大多系统的标准模式(如SSL、IPSec等 )
• 没有已知的并行实现算法
• 需要共同的初始化向量IV
• 存在错误传播现象，一个密文块损坏，影响两个明文块

对CBC模式的攻击：

• 比特反转：如果攻击者截获了传递信息，在这段信息中包含了初始向量IV，根据CBC模式的解密方式我们可以看出，如果攻击者对IV中的任意比特进行反转（1变为0，0变为1），那么明文中相应的比特位就会发生反转。
• 填充提示攻击：当明文长度不为分组长度的整数倍时，需要在最后一个分组中填充一些数据使其凑满一个分组长度。在填充提示攻击中，攻击者会反复发送一段密文，每次发送时都对填充内容进行少许修改。由于接收者（服务器）在无法正确解密时会返回一个错误消息，攻击者通过这个错误消息就可以获取一部分与明文相关的信息，当然这个方法不仅仅适用于CBC模式，而是适用于所有需要进行分组填充的模式。要防御这种攻击，就必须验证密文是否是由合法的发送者在知道明文内容的前提下生成的。

3.3密码反馈CFB（Cipher Feedback）模式

对于AES, DES或任何的分组密码，加密是对一一个b位的分组进行加密。对于DES的例子,b=64,而在AES时，b= 128。但是密文反馈模式(CFB)和输出反馈模式(OFB)及计数器(CTR)模式，亦可将分组密码当成流密码使用。流密码不需要将明文填充到长度是分组长度的整数倍，且可以实时操作。所以，待发送的字符流中任何一个字符都可以用面向字符的流密码加密后立即发送。

适用范围：

• 适用于每次处理r比特明文块的特定需求的加密情形，能灵活适应数据各格式的需要
• 例如：数据库加密要求加密时不能改变明文的字节长度,这时就要以明文字节为单位进行加密

特点：

• 没有已知的并行实现算法
• 隐藏了明文模式
• 需要共同的移位寄存器初始值IV
• 存在错误传播 一个单元损坏影响多个单元

对CFB模式的攻击：

• 重放攻击： Alice向Bob发送了一条消息，这条消息由4个密文分别组成。攻击者将消息的后3个密文分组保存下来，第二天，Alice又向Bob发送了内容不同的4个密文分组（这里我们假设Alice使用的密钥是没有变的）。攻击者将昨天保存下来的3个分组分别替换了这段密文的后3个分组。当Bob解密的时候，4个分组中只有第一个可以解密成功，而第2组就会产生错误，然而第3和第4则被替换成了攻击者保存下来的之前使用过的分组，Bob仍然可以正常解密。此时第2个分组成为了一个错误的分组，但Bob无法确认是网络传输过程中的通信错误，还是被人篡改的。

3.4输出反馈OFB（Output Feedback）模式

OFB模式在结构上类似于CFB模式，但反馈的内容是DES的输出而不是密文，进入移位寄存器的数据和被加密明文无关，只和初始向量相关。

特点：

• 没有已知的并行实现算法
• 需要共同的移位寄存器初始值IV
• 错误传播 一个密文单元损坏只影响对应单元
• 与明文异或的密钥序列最终会重复 64位分组算法,平均重复的周期是2³²

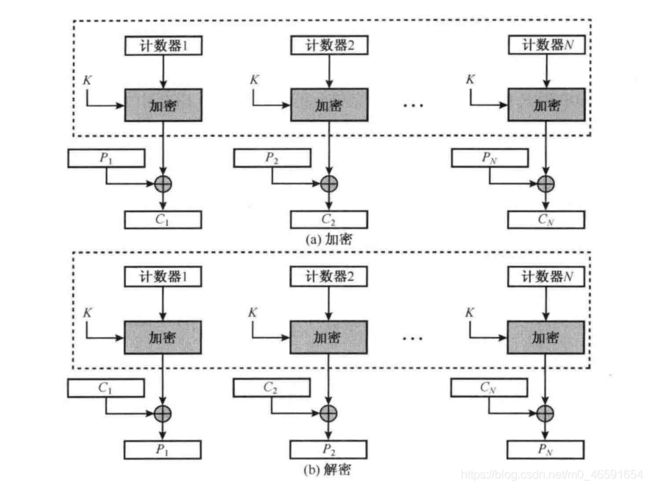
3.5计数器CRT（Counter）模式

利用固定密钥k对自然数序列1,2.3…,n, …加密，将得到的密文分组序列看作密钥流序列，按加法密码的方式与明文分组逐位异或的一种方式。可以利用它产生伪随机数序列，其伪随机特性远比计算机产生的随机数的性质好。

特点：

• 效率
  可并行加密
  预处理
  吞吐量仅受可使用并行数量的限制
• 加密数据块的随机访问
• 可证明安全
• 简单性(只要求实现加密算法)
• 密钥只能使用一次，除非能维持很长的计算器。

3.6四类工作模式比较和选用

ECB模式简单、高速，但最弱，易受重放和替换攻击，一般用于加密长度小于等于分组长度的消息。

CBC, CFB，OFB模式的选用取决于实际的特殊需求。

• 明文不易丢信号，对明文的格式没有特殊要求的环境可选用CBC模式。需要完整性认证功能时也可选用该模式。
• 容易丢信号的环境，或对明文格式有特殊要求的环境，可选用CFB模式。
• 不易丢信号，但信号特别容易错，且明文冗余特别多，可选用OFB模式。

四、相关赛题

4.1

12.25DASCTF.Crypto.asa

#encoding:utf-8
from Crypto.Util.number import bytes_to_long, long_to_bytes, getPrime
import gmpy2, os
from Crypto.Cipher import AES
from flag import flag

assert flag.startswith("DASCTF{") and flag.endswith("}")

def padding(s,blocklen):
    length = (blocklen-len(s)) % blocklen
    return s + chr(length) * length

key = os.urandom(16)
iv = os.urandom(16)
m = padding(flag,16)
c = AES.new(key, AES.MODE_CBC, iv).encrypt(m)
print c.encode("hex")

p = getPrime(512)
q = getPrime(512)
n = p*q
e = 65537
m = bytes_to_long(key)
c = pow(m,e,n)
print hex(n).strip("L")
print hex(c).strip("L")
q = getPrime(512)
n = p*q
m = bytes_to_long(iv)
c = pow(m,e,n)
print hex(n).strip("L")
print hex(c).strip("L")

'''
f8559d671b720cd336f2d8518ad6eac8c405585158dfde74ced376ba42d9fe984d519dc185030ddec7b4dc240fd90fa8
0x661d752110bcc6ee5ca33edaf244716cccce6400dfdbfd84ce6ae2d8fbbeb2f61584da7668768403b6135e7810eae9d4d8e044935f8680de5324c3fc0f9bffb01812f9d2ac9055ee8dbd17b90c5a60cb7595a82f24a075d951db3b7f913b8543ecd52b8c8464ce348c3970d511ae911e814f9ca33b8412db2730e61820f5de47
0xd7931796fa39cfa37c0b621c01175904206dff1d74a28369dcd6517957ed76c5eb7d4934cbeb902119f9215f9ae7926debe3abe856244b45dbb4caaa2b93dbb79a3ca1a9813e1466c49fe3c03e5462811afbf3f40ff79927f9fe3681b7f3cef34466b9a736512f4931b5026eefacbae9be6e408085a7a636c514574c3b22ffe
0x9f159326c907441326c88d17eae1c6e8aaea23922c5e628a585294e379e9245644f9c249c57f54a2b83921b4adc988fecc90c00feb6936d9be1f3a5ffae951b74ffbc6fc7aa11743e4ca179a937392dacf931e820d1d83016562ff608e8c59ef7310654a09bbba4a0129f71dcb61bd9bef073bbb93bfcac4a7a2e81156dbb32d
0x6240740d41a539a88634726cf0a791a87e02419c3c3e00dff62eba59e81a93fd04a59109e57f64fc375b9a321583b6fa133317eb5c4e6eb1e6f6d9a0b4ae6ff0c54423718811f7956cd63b7bf9c7f8e29f48dad8f05b63b71d6c5112d91864adba0d6bb342c67aee39ccd5e2a6928a8e4ab2248d29a0c990bae821b31b39b1f3
'''

本题涉及到CBC加密模式和RSA的相关知识。
可以发现参数生成过程中两次使用了相同的p，所以先求是两个n的最大公约数得到p，然后进行RSA基础解密得到key和iv，再进行AES的CBC模式解密即可。

from gmpy2 import*
from Crypto.Util.number import *
from Crypto.Cipher import AES
n1=0x661d752110bcc6ee5ca33edaf244716cccce6400dfdbfd84ce6ae2d8fbbeb2f61584da7668768403b6135e7810eae9d4d8e044935f8680de5324c3fc0f9bffb01812f9d2ac9055ee8dbd17b90c5a60cb7595a82f24a075d951db3b7f913b8543ecd52b8c8464ce348c3970d511ae911e814f9ca33b8412db2730e61820f5de47
n2=0x9f159326c907441326c88d17eae1c6e8aaea23922c5e628a585294e379e9245644f9c249c57f54a2b83921b4adc988fecc90c00feb6936d9be1f3a5ffae951b74ffbc6fc7aa11743e4ca179a937392dacf931e820d1d83016562ff608e8c59ef7310654a09bbba4a0129f71dcb61bd9bef073bbb93bfcac4a7a2e81156dbb32d

p=gcd(n1,n2)
print(p)

p=9540203717217880059997385799331301649727503984010337568404427747385824530958536656147747848448822264268428226235860927158082497191830274046098671199542207

q1=n1//p
q2=n2//p

q1=7516363572069282672026207933559652178219500346572833541898291914709599489663099294873864325874446529790989623154562433650903688205637808143655002021347193
q2=11709684761787285321169271535544195271858094227802343600689046124468724036061594373710783769953414491363505203702886296365059403955548433247809736064179219
c1=0xd7931796fa39cfa37c0b621c01175904206dff1d74a28369dcd6517957ed76c5eb7d4934cbeb902119f9215f9ae7926debe3abe856244b45dbb4caaa2b93dbb79a3ca1a9813e1466c49fe3c03e5462811afbf3f40ff79927f9fe3681b7f3cef34466b9a736512f4931b5026eefacbae9be6e408085a7a636c514574c3b22ffe
c2=0x6240740d41a539a88634726cf0a791a87e02419c3c3e00dff62eba59e81a93fd04a59109e57f64fc375b9a321583b6fa133317eb5c4e6eb1e6f6d9a0b4ae6ff0c54423718811f7956cd63b7bf9c7f8e29f48dad8f05b63b71d6c5112d91864adba0d6bb342c67aee39ccd5e2a6928a8e4ab2248d29a0c990bae821b31b39b1f3
e=65537


d1=inverse(e,(p - 1) * (q1 - 1))
key=pow(c1,d1,n1)
d2=inverse(e,(p - 1) * (q2 - 1))
iv=pow(c2,d2,n2)

c=0xf8559d671b720cd336f2d8518ad6eac8c405585158dfde74ced376ba42d9fe984d519dc185030ddec7b4dc240fd90fa8
key=0x8929ef12a17f145bc9b48afa2c88a2ef
iv=0xf5f6a88b0855ed47e0de771caf3cb23e

key=long_to_bytes(key)
iv=long_to_bytes(iv)
c=long_to_bytes(c)

aes=AES.new(key,AES.MODE_CBC,iv)
print(aes.decrypt(c))
#b'DASCTF{e4f6c51dc2fe722173e41b47533879bc}\x08\x08\x08\x08\x08\x08\x08\x08'

4.2

题目链接buu平台

本题用到的是AES的CBC模式。

from Cryptodome.Cipher import AES
import os
import gmpy2
from flag import FLAG
from Cryptodome.Util.number import *

def main():
    key=os.urandom(2)*16
    iv=os.urandom(16)
    print(bytes_to_long(key)^bytes_to_long(iv))
    aes=AES.new(key,AES.MODE_CBC,iv)
    enc_flag = aes.encrypt(FLAG)
    print(enc_flag)
if __name__=="__main__":
    main()

key是产生的两个字节的随机比特流重复16次得到的，iv是一个长度为16字节的随机比特流。由key和iv异或的输出结果可得，key的低16字节与iv的16字节异或，高16字节被保留。

key和iv异或的输出结果转为16进制值可以发现重复的字节是b’\xc9\x81’，然后计算iv之后进行AES的CBC模式解密即可。

from Crypto.Util.number import *
from Crypto.Cipher import AES

xor=91144196586662942563895769614300232343026691029427747065707381728622849079757
c=b'\x8c-\xcd\xde\xa7\xe9\x7f.b\x8aKs\xf1\xba\xc75\xc4d\x13\x07\xac\xa4&\xd6\x91\xfe\xf3\x14\x10|\xf8p'

print(hex(xor))
# xor=0xc981c981c981c981c981c981c981c9814eed98e380b1356763849930c850b9cd
key=b'\xc9\x81'*16
iv=(long_to_bytes(xor^bytes_to_long(key)))
aes=AES.new(key,AES.MODE_CBC,iv)
flag=aes.decrypt(c)
print(flag)
#b'actf{W0W_y0u_can_so1v3_AES_now!}'