深度学习笔记其六：现代卷积神经网络和PYTORCH

Reference：

1. 《动手学深度学习》 强烈建议看原书

文章跳转：

1. 深度学习笔记其一：基础知识和PYTORCH
2. 深度学习笔记其二：线性神经网络和PYTORCH
3. 深度学习笔记其三：多层感知机和PYTORCH
4. 深度学习笔记其四：深度学习计算和PYTORCH
5. 深度学习笔记其五：卷积神经网络和PYTORCH
6. 深度学习笔记其六：现代卷积神经网络和PYTORCH
7. 深度学习笔记其七：计算机视觉和PYTORCH

上一章我们介绍了卷积神经网络的基本原理，本章我们将带你了解现代的卷积神经网络架构，许多现代卷积神经网络的研究都是建立在这一章的基础上的。在本章中的每一个模型都曾一度占据主导地位，其中许多模型都是ImageNet竞赛的优胜者。ImageNet竞赛自2010年以来，一直是计算机视觉中监督学习进展的指向标。

这些模型包括：

• AlexNet。它是第一个在大规模视觉竞赛中击败传统计算机视觉模型的大型神经网络；
• 使用重复块的网络（VGG）。它利用许多重复的神经网络块；
• 网络中的网络（NiN）。它重复使用由卷积层和 $1\times 1$ 卷积层（用来代替全连接层）来构建深层网络；
• 含并行连结的网络（GoogLeNet）。它使用并行连结的网络，通过不同窗口大小的卷积层和最大汇聚层来并行抽取信息；
• 残差网络（ResNet）。它通过残差块构建跨层的数据通道，是计算机视觉中最流行的体系架构；
• 稠密连接网络（DenseNet）。它的计算成本很高，但给我们带来了更好的效果。

虽然深度神经网络的概念非常简单——将神经网络堆叠在一起。但由于不同的网络架构和超参数选择，这些神经网络的性能会发生很大变化。本章介绍的神经网络是将人类直觉和相关数学见解结合后，经过大量研究试错后的结晶。我们会按时间顺序介绍这些模型，在追寻历史的脉络的同时，帮助你培养对该领域发展的直觉。这将有助于你研究开发自己的架构。例如，本章介绍的批量规范化（batch normalization）和残差网络（ResNet）为设计和训练深度神经网络提供了重要思想指导。

1. 深度卷积神经网络（AlexNet）

在LeNet提出后，卷积神经网络在计算机视觉和机器学习领域中很有名气。但卷积神经网络并没有主导这些领域。这是因为虽然LeNet在小数据集上取得了很好的效果，但是在更大、更真实的数据集上训练卷积神经网络的性能和可行性还有待研究。事实上，在上世纪90年代初到2012年之间的大部分时间里，神经网络往往被其他机器学习方法超越，如支持向量机（support vector machines）。

在计算机视觉中，直接将神经网络与其他机器学习方法进行比较也许不公平。这是因为，卷积神经网络的输入是由原始像素值或是经过简单预处理（例如居中、缩放）的像素值组成的。但在使用传统机器学习方法时，从业者永远不会将原始像素作为输入。在传统机器学习方法中，计算机视觉流水线是由经过人的手工精心设计的特征流水线组成的。对于这些传统方法，大部分的进展都来自于对特征有了更聪明的想法，并且学习到的算法往往归于事后的解释。

虽然上世纪90年代就有了一些神经网络加速卡，但仅靠它们还不足以开发出有大量参数的深层多通道多层卷积神经网络。此外，当时的数据集仍然相对较小。除了这些障碍，训练神经网络的一些关键技巧仍然缺失，包括启发式参数初始化、随机梯度下降的变体、非挤压激活函数和有效的正则化技术。

因此，与训练端到端（从像素到分类结果）系统不同，经典机器学习的流水线看起来更像下面这样：

1. 获取一个有趣的数据集。在早期，收集这些数据集需要昂贵的传感器（在当时最先进的图像也就100万像素）。
2. 根据光学、几何学、其他知识以及偶然的发现，手工对特征数据集进行预处理。
3. 通过标准的特征提取算法，如 SIFT（尺度不变特征变换） [Lowe, 2004]和 SURF（加速鲁棒特征） [Bay et al., 2006]或其他手动调整的流水线来输入数据。
4. 将提取的特征送入最喜欢的分类器中（例如线性模型或其它核方法），以训练分类器。

如果你和机器学习研究人员交谈，你会发现他们相信机器学习既重要又美丽：优雅的理论去证明各种模型的性质。机器学习是一个正在蓬勃发展、严谨且非常有用的领域。然而，如果你和计算机视觉研究人员交谈，你会听到一个完全不同的故事。他们会告诉你图像识别的诡异事实————推动领域进步的是数据特征，而不是学习算法。计算机视觉研究人员相信，从对最终模型精度的影响来说，更大或更干净的数据集、或是稍微改进的特征提取，比任何学习算法带来的进步要大得多。

1.1 学习表征

另一种预测这个领域发展的方法————观察图像特征的提取方法。在2012年前，图像特征都是机械地计算出来的。事实上，设计一套新的特征函数、改进结果，并撰写论文是盛极一时的潮流。SIFT [Lowe, 2004]、SURF [Bay et al., 2006]、HOG（定向梯度直方图） [Dalal & Triggs, 2005]、bags of visual words和类似的特征提取方法占据了主导地位。

另一组研究人员，包括Yann LeCun、Geoff Hinton、Yoshua Bengio、Andrew Ng、Shun ichi Amari和Juergen Schmidhuber，想法则与众不同：他们认为特征本身应该被学习。此外，他们还认为，在合理地复杂性前提下，特征应该由多个共同学习的神经网络层组成，每个层都有可学习的参数。在机器视觉中，最底层可能检测边缘、颜色和纹理。事实上，Alex Krizhevsky、Ilya Sutskever和Geoff Hinton提出了一种新的卷积神经网络变体AlexNet。在2012年ImageNet挑战赛中取得了轰动一时的成绩。AlexNet以Alex Krizhevsky的名字命名，他是论文 [Krizhevsky et al., 2012]的第一作者。

有趣的是，在网络的最底层，模型学习到了一些类似于传统滤波器的特征抽取器。下图是从AlexNet论文 [Krizhevsky et al., 2012]复制的，描述了底层图像特征。

AlexNet 第一层学习到的特征抽取器

AlexNet 的更高层建立在这些底层表示的基础上，以表示更大的特征，如眼睛、鼻子、草叶等等。而更高的层可以检测整个物体，如人、飞机、狗或飞盘。最终的隐藏神经元可以学习图像的综合表示，从而使属于不同类别的数据易于区分。尽管一直有一群执着的研究者不断钻研，试图学习视觉数据的逐级表征，然而很长一段时间里这些尝试都未有突破。深度卷积神经网络的突破出现在 2012 年。突破可归因于两个关键因素。

1.1 缺少的成分：数据

包含许多特征的深度模型需要大量的有标签数据，才能显著优于基于凸优化的传统方法（如线性方法和核方法，也就是核方法是凸优化方法）。然而，限于早期计算机有限的存储和90年代有限的研究预算，大部分研究只基于小的公开数据集。例如，不少研究论文基于加州大学欧文分校（UCI）提供的若干个公开数据集，其中许多数据集只有几百至几千张在非自然环境下以低分辨率拍摄的图像。这一状况在2010年前后兴起的大数据浪潮中得到改善。2009年，ImageNet数据集发布，并发起ImageNet挑战赛：要求研究人员从100万个样本中训练模型，以区分1000个不同类别的对象。ImageNet数据集由斯坦福教授李飞飞小组的研究人员开发，利用谷歌图像搜索（Google Image Search）对每一类图像进行预筛选，并利用亚马逊众包（Amazon Mechanical Turk）来标注每张图片的相关类别。这种规模是前所未有的。这项被称为ImageNet的挑战赛推动了计算机视觉和机器学习研究的发展，挑战研究人员确定哪些模型能够在更大的数据规模下表现最好。

1.2 缺少的成分：硬件

深度学习对计算资源要求很高，训练可能需要数百个迭代轮数，每次迭代都需要通过代价高昂的许多线性代数层传递数据。这也是为什么在20世纪90年代至21世纪初，优化凸目标的简单算法是研究人员的首选。然而，用GPU训练神经网络改变了这一格局。图形处理器（Graphics Processing Unit，GPU）早年用来加速图形处理，使电脑游戏玩家受益。GPU可优化高吞吐量的 $4\times 4$ 矩阵和向量乘法，从而服务于基本的图形任务。幸运的是，这些数学运算与卷积层的计算惊人地相似。由此，英伟达（NVIDIA）和ATI已经开始为通用计算操作优化gpu，甚至把它们作为通用GPU（general-purpose GPUs，GPGPU）来销售。

那么 GPU 比 CPU 强在哪里呢？

首先，我们深度理解一下中央处理器(Central Processing Unit，CPU)的核心。CPU的每个核心都拥有高时钟频率的运行能力，和高达数MB的三级缓存（L3Cache）。它们非常适合执行各种指令，具有分支预测器、深层流水线和其他使CPU能够运行各种程序的功能。然而，这种明显的优势也是它的致命弱点：通用核心的制造成本非常高。它们需要大量的芯片面积、复杂的支持结构（内存接口、内核之间的缓存逻辑、高速互连等等），而且它们在任何单个任务上的性能都相对较差。现代笔记本电脑最多有4核，即使是高端服务器也很少超过64核，因为它们的性价比不高。

相比于 CPU，GPU 由 $100$~$1000$ 个小的处理单元组成（NVIDIA、ATI、ARM和其他芯片供应商之间的细节稍有不同），通常被分成更大的组（NVIDIA称之为warps）。虽然每个GPU核心都相对较弱，有时甚至以低于1GHz的时钟频率运行，但庞大的核心数量使 GPU 比 CPU 快几个数量级。例如，NVIDIA 最近一代的 Ampere GPU架构为每个芯片提供了高达 312 TFlops的浮点性能，而CPU的浮点性能到目前为止还没有超过1 TFlops。之所以有如此大的差距，原因其实很简单：首先，功耗往往会随时钟频率呈二次方增长。对于一个CPU核心，假设它的运行速度比GPU快4倍，你可以使用16个GPU内核取代，那么GPU的综合性能就是CPU的 $16\times 1/4=4$ 倍。其次，GPU内核要简单得多，这使得它们更节能。此外，深度学习中的许多操作需要相对较高的内存带宽，而GPU拥有10倍于CPU的带宽。

回到2012年的重大突破，当Alex Krizhevsky和Ilya Sutskever实现了可以在GPU硬件上运行的深度卷积神经网络时，一个重大突破出现了。他们意识到卷积神经网络中的计算瓶颈：卷积和矩阵乘法，都是可以在硬件上并行化的操作。于是，他们使用两个显存为3GB的NVIDIA GTX580 GPU实现了快速卷积运算。他们的创新cuda-convnet几年来它一直是行业标准，并推动了深度学习热潮。

1.2 AlexNet

2012年，AlexNet横空出世。它首次证明了学习到的特征可以超越手工设计的特征。它一举打破了计算机视觉研究的现状。AlexNet使用了8层卷积神经网络，并以很大的优势赢得了2012年ImageNet图像识别挑战赛。

AlexNet和LeNet的架构非常相似，如下图所示。注意，这里我们提供了一个稍微精简版本的AlexNet，去除了当年需要两个小型GPU同时运算的设计特点。

从 LeNet(左)到 AlexNet(右)

AlexNet和LeNet的设计理念非常相似，但也存在显著差异。首先，AlexNet 比相对较小的 LeNet 五层要深得多。AlexNet 由八层组成：五个卷积层、两个全连接隐藏层和一个全连接输出层。其次，AlexNet 使用 ReLU 而不是 sigmoid 作为其激活函数。下面，让我们深入研究 AlexNet 的细节。

1.2.1 模型设计

在 AlexNet 的第一层，卷积窗口的形状是 $11\times 11$。由于 ImageNet 中大多数图像的宽和高比 MNIST 图像的多 $10$ 倍以上，因此，需要一个更大的卷积窗口来捕获目标。第二层中的卷积窗口形状被缩减为 $5\times 5$，然后是 $3\times 3$。此外，在第一层、第二层和第五层卷积层之后，加入窗口形状为 $3\times 3$、步幅为 $2$ 的最大汇聚层。而且，AlexNet 的卷积通道数目是 LeNet 的 $10$ 倍。

在最后一个卷积层后有两个全连接层，分别有 $4096$ 个输出。这两个巨大的全连接层拥有将近1GB的模型参数。由于早期GPU 显存有限，原版的 AlexNet 采用了双数据流设计，使得每个 GPU 只负责存储和计算模型的一半参数。幸运的是，现在 GPU 显存相对充裕，所以我们现在很少需要跨 GPU 分解模型（因此，我们的 AlexNet 模型在这方面与原始论文稍有不同）。

1.2.2 激活函数

此外，AlexNet 将 sigmoid 激活函数改为更简单的 ReLU 激活函数。一方面，ReLU 激活函数的计算更简单，它不需要如 sigmoid 激活函数那般复杂的求幂运算。另一方面，当使用不同的参数初始化方法时，ReLU 激活函数使训练模型更加容易。 当 sigmoid 激活函数的输出非常接近于 $0$ 或 $1$ 时，这些区域的梯度几乎为 $0$，因此反向传播无法继续更新一些模型参数。相反，ReLU激活函数在正区间的梯度总是 $1$。因此，如果模型参数没有正确初始化，sigmoid 函数可能在正区间内得到几乎为 $0$ 的梯度，从而使模型无法得到有效的训练。

1.2.3 容量控制和预处理

AlexNet 通过暂退法控制全连接层的模型复杂度，而 LeNet 只使用了权重衰减。为了进一步扩充数据，AlexNet 在训练时增加了大量的图像增强数据，如翻转、裁切和变色。这使得模型更健壮，更大的样本量有效地减少了过拟合。我们将在后面章节中更详细地讨论数据扩增。

import torch
from torch import nn
from d2l import torch as d2l

net = nn.Sequential(
    # 这里，我们使用一个11*11的更大窗口来捕捉对象。
    # 同时，步幅为4，以减少输出的高度和宽度。
    # 另外，输出通道的数目远大于LeNet
    nn.Conv2d(1, 96, kernel_size=11, stride=4, padding=1), nn.ReLU(),
    nn.MaxPool2d(kernel_size=3, stride=2),
    # 减小卷积窗口，使用填充为2来使得输入与输出的高和宽一致，且增大输出通道数
    nn.Conv2d(96, 256, kernel_size=5, padding=2), nn.ReLU(),
    nn.MaxPool2d(kernel_size=3, stride=2),
    # 使用三个连续的卷积层和较小的卷积窗口。
    # 除了最后的卷积层，输出通道的数量进一步增加。
    # 在前两个卷积层之后，汇聚层不用于减少输入的高度和宽度
    nn.Conv2d(256, 384, kernel_size=3, padding=1), nn.ReLU(),
    nn.Conv2d(384, 384, kernel_size=3, padding=1), nn.ReLU(),
    nn.Conv2d(384, 256, kernel_size=3, padding=1), nn.ReLU(),
    nn.MaxPool2d(kernel_size=3, stride=2),
    nn.Flatten(),
    # 这里，全连接层的输出数量是LeNet中的好几倍。使用dropout层来减轻过拟合
    nn.Linear(6400, 4096), nn.ReLU(),
    nn.Dropout(p=0.5),
    nn.Linear(4096, 4096), nn.ReLU(),
    nn.Dropout(p=0.5),
    # 最后是输出层。由于这里使用Fashion-MNIST，所以用类别数为10，而非论文中的1000
    nn.Linear(4096, 10))

我们构造一个高度和宽度都为 $224$ 的单通道数据，来观察每一层输出的形状。它与上面图片中的 AlexNet 架构相匹配。

X = torch.randn(1, 1, 224, 224)
for layer in net:
    X=layer(X)
    print(layer.__class__.__name__,'output shape:\t',X.shape)

Conv2d output shape: torch.Size([1, 96, 54, 54])
ReLU output shape: torch.Size([1, 96, 54, 54])
MaxPool2d output shape: torch.Size([1, 96, 26, 26])
Conv2d output shape: torch.Size([1, 256, 26, 26])
ReLU output shape: torch.Size([1, 256, 26, 26])
MaxPool2d output shape: torch.Size([1, 256, 12, 12])
Conv2d output shape: torch.Size([1, 384, 12, 12])
ReLU output shape: torch.Size([1, 384, 12, 12])
Conv2d output shape: torch.Size([1, 384, 12, 12])
ReLU output shape: torch.Size([1, 384, 12, 12])
Conv2d output shape: torch.Size([1, 256, 12, 12])
ReLU output shape: torch.Size([1, 256, 12, 12])
MaxPool2d output shape: torch.Size([1, 256, 5, 5])
Flatten output shape: torch.Size([1, 6400])
Linear output shape: torch.Size([1, 4096])
ReLU output shape: torch.Size([1, 4096])
Dropout output shape: torch.Size([1, 4096])
Linear output shape: torch.Size([1, 4096])
ReLU output shape: torch.Size([1, 4096])
Dropout output shape: torch.Size([1, 4096])
Linear output shape: torch.Size([1, 10])

1.3 读取数据集

尽管本文中 AlexNet 是在 ImageNet 上进行训练的，但我们在这里使用的是 Fashion-MNIST 数据集。因为即使在现代 GPU 上，训练 ImageNet 模型，同时使其收敛可能需要数小时或数天的时间。将 AlexNet 直接应用于 Fashion-MNIST 的一个问题是，Fashion-MNIST 图像的分辨率（$28\times 28$ 像素）低于 ImageNet 图像。为了解决这个问题，我们将它们增加到 $224\times 224$（通常来讲这不是一个明智的做法，但我们在这里这样做是为了有效使用 AlexNet 架构）。我们使用 d2l.load_data_fashion_mnist 函数中的 resize 参数执行此调整。

batch_size = 128
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size, resize=224)

1.4 训练AlexNet

现在，我们可以开始训练 AlexNet 了。与上一篇文章中的 LeNet 相比，这里的主要变化是使用更小的学习速率训练，这是因为网络更深更广、图像分辨率更高，训练卷积神经网络就更昂贵。

lr, num_epochs = 0.01, 10
d2l.train_ch6(net, train_iter, test_iter, num_epochs, lr, d2l.try_gpu())

loss 0.327, train acc 0.881, test acc 0.885
4149.6 examples/sec on cuda:0

1.5 小结

• AlexNet 的架构与 LeNet 相似，但使用了更多的卷积层和更多的参数来拟合大规模的 ImageNet 数据集。
• 今天，AlexNet 已经被更有效的架构所超越，但它是从浅层网络到深层网络的关键一步。
• 尽管 AlexNet 的代码只比 LeNet 多出几行，但学术界花了很多年才接受深度学习这一概念，并应用其出色的实验结果。这也是由于缺乏有效的计算工具。
• Dropout、ReLU 和预处理是提升计算机视觉任务性能的其他关键步骤。

2. 使用块的网络（VGG）

虽然AlexNet证明深层神经网络卓有成效，但它没有提供一个通用的模板来指导后续的研究人员设计新的网络。在下面的几个章节中，我们将介绍一些常用于设计深层神经网络的启发式概念。

与芯片设计中工程师从放置晶体管到逻辑元件再到逻辑块的过程类似，神经网络架构的设计也逐渐变得更加抽象。研究人员开始从单个神经元的角度思考问题，发展到整个层，现在又转向块，重复层的模式。

使用块的想法首先出现在牛津大学的视觉几何组（visualgeometry group）的VGG网络中。通过使用循环和子程序，可以很容易地在任何现代深度学习框架的代码中实现这些重复的架构。

2.1 VGG块

经典卷积神经网络的基本组成部分是下面的这个序列：

1. 带填充以保持分辨率的卷积层；
2. 非线性激活函数，如 ReLU；
3. 汇聚层，如最大汇聚层。

而一个 VGG 块与之类似，由一系列卷积层组成，后面再加上用于空间下采样的最大汇聚层。在最初的 VGG 论文中 [Simonyan & Zisserman, 2014]，作者使用了带有 $3\times 3$ 卷积核、填充为 $1$（保持高度和宽度）的卷积层，和带有 $2\times 2$ 汇聚窗口、步幅为 $2$（每个块后的分辨率减半）的最大汇聚层。在下面的代码中，我们定义了一个名为 vgg_block 的函数来实现一个 VGG 块。

该函数有三个参数，分别对应于 卷积层的数量(num_convs)、输入通道的数量(in_channels) 和 (输出通道的数量out_channels)。

import torch
from torch import nn
from d2l import torch as d2l


def vgg_block(num_convs, in_channels, out_channels):
    layers = []
    for _ in range(num_convs):
        layers.append(nn.Conv2d(in_channels, out_channels,
                                kernel_size=3, padding=1))
        layers.append(nn.ReLU())
        in_channels = out_channels
    layers.append(nn.MaxPool2d(kernel_size=2,stride=2))
    return nn.Sequential(*layers)

2.2 VGG网络

与 AlexNet、LeNet 一样，VGG 网络可以分为两部分：第一部分主要由卷积层和汇聚层组成，第二部分由全连接层组成。如下图所示：

从AlexNet到VGG，它们本质上都是块设计。

VGG神经网络连接图中的几个VGG块（在vgg_block函数中定义）。其中有超参数变量conv_arch。该变量指定了每个VGG块(注意是块不是层)里卷积层个数和输出通道数。全连接模块则与AlexNet中的相同。

原始VGG网络有5个卷积块，其中前两个块各有一个卷积层，后三个块各包含两个卷积层。第一个模块有 $64$ 个输出通道，每个后续模块将输出通道数量翻倍，直到该数字达到 $512$。由于该网络使用 $8$ 个卷积层和 $3$ 个全连接层，因此它通常被称为VGG-11。

conv_arch = ((1, 64), (1, 128), (2, 256), (2, 512), (2, 512))

下面的代码实现了VGG-11。可以通过在 conv_arch 上执行 for 循环来简单实现。

def vgg(conv_arch):
    conv_blks = []
    in_channels = 1
    # 卷积层部分
    for (num_convs, out_channels) in conv_arch:
        conv_blks.append(vgg_block(num_convs, in_channels, out_channels))
        in_channels = out_channels

    return nn.Sequential(
        *conv_blks, nn.Flatten(),
        # 全连接层部分
        nn.Linear(out_channels * 7 * 7, 4096), nn.ReLU(), nn.Dropout(0.5),
        nn.Linear(4096, 4096), nn.ReLU(), nn.Dropout(0.5),
        nn.Linear(4096, 10))

net = vgg(conv_arch)

接下来，我们将构建一个高度和宽度为 $224$ 的单通道数据样本，以观察每个层输出的形状。

X = torch.randn(size=(1, 1, 224, 224))
for blk in net:
    X = blk(X)
    print(blk.__class__.__name__,'output shape:\t',X.shape)

Sequential output shape: torch.Size([1, 64, 112, 112])
Sequential output shape: torch.Size([1, 128, 56, 56])
Sequential output shape: torch.Size([1, 256, 28, 28])
Sequential output shape: torch.Size([1, 512, 14, 14])
Sequential output shape: torch.Size([1, 512, 7, 7])
Flatten output shape: torch.Size([1, 25088])
Linear output shape: torch.Size([1, 4096])
ReLU output shape: torch.Size([1, 4096])
Dropout output shape: torch.Size([1, 4096])
Linear output shape: torch.Size([1, 4096])
ReLU output shape: torch.Size([1, 4096])
Dropout output shape: torch.Size([1, 4096])
Linear output shape: torch.Size([1, 10])

正如你所看到的，我们在每个块的高度和宽度减半，最终高度和宽度都为 $7$。最后再展平表示，送入全连接层处理。

2.3 训练模型

由于 VGG-11 比 AlexNet 计算量更大，因此我们构建了一个通道数较少的网络，足够用于训练 Fashion-MNIST 数据集。

ratio = 4
small_conv_arch = [(pair[0], pair[1] // ratio) for pair in conv_arch]
net = vgg(small_conv_arch)

除了使用略高的学习率外，模型训练过程与 AlexNet 类似。

lr, num_epochs, batch_size = 0.05, 10, 128
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size, resize=224)
d2l.train_ch6(net, train_iter, test_iter, num_epochs, lr, d2l.try_gpu())

loss 0.177, train acc 0.934, test acc 0.911
2562.3 examples/sec on cuda:0

2.4 小结

• VGG-11 使用可复用的卷积块构造网络。不同的VGG模型可通过每个块中卷积层数量和输出通道数量的差异来定义。
• 块的使用导致网络定义的非常简洁。使用块可以有效地设计复杂的网络。
• 在VGG论文中，Simonyan 和 Ziserman 尝试了各种架构。特别是他们发现深层且窄的卷积（即 $3\times 3$）比较浅层且宽的卷积更有效。

3. 网络中的网络（NiN）

LeNet、AlexNet 和 VGG 都有一个共同的设计模式：通过一系列的卷积层与汇聚层来提取空间结构特征；然后通过全连接层对特征的表征进行处理。AlexNet 和 VGG 对 LeNet 的改进主要在于如何扩大和加深这两个模块。或者，可以想象在这个过程的早期使用全连接层。然而，如果使用了全连接层，可能会完全放弃表征的空间结构。网络中的网络（NiN）提供了一个非常简单的解决方案：在每个像素的通道上分别使用多层感知机 [Lin et al., 2013]

3.1 NiN块

回想一下，卷积层的输入和输出由四维张量组成，张量的每个轴分别对应样本、通道、高度和宽度。另外，全连接层的输入和输出通常是分别对应于样本和特征的二维张量。NiN 的想法是在每个像素位置（针对每个高度和宽度）应用一个全连接层。如果我们将权重连接到每个空间位置，我们可以将其视为 $1\times 1$ 卷积层（上一个笔记中提到过），或作为在每个像素位置上独立作用的全连接层。从另一个角度看，即将空间维度中的每个像素视为单个样本，将通道维度视为不同特征（feature）。

下图说明了 VGG 和 NiN 及它们的块之间主要架构差异。NiN 块以一个普通卷积层开始，后面是两个 $1\times 1$ 的卷积层。这两个 $1\times 1$ 卷积层充当带有 ReLU 激活函数的逐像素全连接层($1\times 1$卷积的唯一计算发生在通道上)。第一层的卷积窗口形状通常由用户设置。随后的卷积窗口形状固定为 $1\times 1$。

对比 VGG 和 NiN 及它们的块之间主要架构差异。

import torch
from torch import nn
from d2l import torch as d2l


def nin_block(in_channels, out_channels, kernel_size, strides, padding):
    return nn.Sequential(
        nn.Conv2d(in_channels, out_channels, kernel_size, strides, padding),
        nn.ReLU(),
        nn.Conv2d(out_channels, out_channels, kernel_size=1), nn.ReLU(),
        nn.Conv2d(out_channels, out_channels, kernel_size=1), nn.ReLU())

3.2 NiN模型

最初的 NiN 网络是在 AlexNet 后不久提出的，显然从中得到了一些启示。NiN 使用窗口形状为 $11\times 11$、$5\times 5$ 和 $3\times 3$ 的卷积层，输出通道数量与 AlexNet 中的相同。每个 NiN 块后有一个最大汇聚层，汇聚窗口形状为 $3\times 3$，步幅为 $2$。

NiN 和 AlexNet 之间的一个显著区别是 NiN 完全取消了全连接层。相反，NiN 使用一个 NiN 块，其输出通道数等于标签类别的数量。最后放一个全局平均汇聚层(global average pooling layer)，生成一个对数几率(logits)。NiN 设计的一个优点是，它显著减少了模型所需参数的数量。然而，在实践中，这种设计有时会增加训练模型的时间。

net = nn.Sequential(
    nin_block(1, 96, kernel_size=11, strides=4, padding=0),
    nn.MaxPool2d(3, stride=2),
    nin_block(96, 256, kernel_size=5, strides=1, padding=2),
    nn.MaxPool2d(3, stride=2),
    nin_block(256, 384, kernel_size=3, strides=1, padding=1),
    nn.MaxPool2d(3, stride=2),
    nn.Dropout(0.5),
    # 标签类别数是10
    nin_block(384, 10, kernel_size=3, strides=1, padding=1),
    nn.AdaptiveAvgPool2d((1, 1)),
    # 将四维的输出转成二维的输出，其形状为(批量大小,10)
    nn.Flatten())

我们创建一个数据样本来查看每个块的输出形状。

X = torch.rand(size=(1, 1, 224, 224))
for layer in net:
    X = layer(X)
    print(layer.__class__.__name__,'output shape:\t', X.shape)

Sequential output shape: torch.Size([1, 96, 54, 54])
MaxPool2d output shape: torch.Size([1, 96, 26, 26])
Sequential output shape: torch.Size([1, 256, 26, 26])
MaxPool2d output shape: torch.Size([1, 256, 12, 12])
Sequential output shape: torch.Size([1, 384, 12, 12])
MaxPool2d output shape: torch.Size([1, 384, 5, 5])
Dropout output shape: torch.Size([1, 384, 5, 5])
Sequential output shape: torch.Size([1, 10, 5, 5])
AdaptiveAvgPool2d output shape: torch.Size([1, 10, 1, 1])
Flatten output shape: torch.Size([1, 10])

3.3 训练模型

和以前一样，我们使用 Fashion-MNIST 来训练模型。训练 NiN 与训练 AlexNet、VGG 时相似。

lr, num_epochs, batch_size = 0.1, 10, 128
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size, resize=224)
d2l.train_ch6(net, train_iter, test_iter, num_epochs, lr, d2l.try_gpu())

loss 0.363, train acc 0.865, test acc 0.879
3212.2 examples/sec on cuda:0

3.4 小结

• NiN 使用由一个卷积层和多个 $1\times 1$ 卷积层组成的块。该块可以在卷积神经网络中使用，以允许更多的每像素非线性。
• NiN 去除了容易造成过拟合的全连接层，将它们替换为全局平均汇聚层（即在所有位置上进行求和）。该汇聚层通道数量为所需的输出数量（例如，Fashion-MNIST的输出为10）。
• 移除全连接层可减少过拟合，同时显著减少 NiN 的参数。
• NiN 的设计影响了许多后续卷积神经网络的设计。

4. 含并行连结的网络（GoogLeNet）

在$2014$年的 ImageNet 图像识别挑战赛中，一个名叫 GoogLeNet [Szegedy et al., 2015]的网络架构大放异彩。GoogLeNet 吸收了 NiN 中串联网络的思想，并在此基础上做了改进。这篇论文的一个重点是解决了什么样大小的卷积核最合适的问题。毕竟，以前流行的网络使用小到 $1\times 1$，大到的卷积核 $11\times 11$。本文的一个观点是，有时使用不同大小的卷积核组合(注意是使用的组合)是有利的。在本节中，我们将介绍一个稍微简化的 GoogLeNet 版本：我们省略了一些为稳定训练而添加的特殊特性，现在有了更好的训练方法，这些特性不是必要的。

4.1 Inception块

在 GoogLeNet 中，基本的卷积块被称为Inception块（Inception block）。这很可能得名于电影《盗梦空间》（Inception），因为电影中的一句话“我们需要走得更深”（“We need to go deeper”）。

Inception块的架构。

如上图所示，Inception 块由四条并行路径组成。前三条路径使用窗口大小为 $1\times 1$、$3\times 3$ 和 $5\times 5$ 的卷积层，从不同空间大小中提取信息。中间的两条路径在输入上执行 $1\times 1$ 卷积，以减少通道数，从而降低模型的复杂性。第四条路径使用 $3\times 3$ 最大汇聚层，然后使用 $1\times 1$ 卷积层来改变通道数。这四条路径都使用合适的填充来使输入与输出的高和宽一致，最后我们将每条线路的输出在通道维度上连结，并构成 Inception 块的输出。在 Inception 块中，通常调整的超参数是每层输出通道数。

import torch
from torch import nn
from torch.nn import functional as F
from d2l import torch as d2l


class Inception(nn.Module):
    # c1--c4是每条路径的输出通道数
    def __init__(self, in_channels, c1, c2, c3, c4, **kwargs):
        super(Inception, self).__init__(**kwargs)
        # 线路1，单1x1卷积层
        self.p1_1 = nn.Conv2d(in_channels, c1, kernel_size=1)
        # 线路2，1x1卷积层后接3x3卷积层
        self.p2_1 = nn.Conv2d(in_channels, c2[0], kernel_size=1)
        self.p2_2 = nn.Conv2d(c2[0], c2[1], kernel_size=3, padding=1)
        # 线路3，1x1卷积层后接5x5卷积层
        self.p3_1 = nn.Conv2d(in_channels, c3[0], kernel_size=1)
        self.p3_2 = nn.Conv2d(c3[0], c3[1], kernel_size=5, padding=2)
        # 线路4，3x3最大汇聚层后接1x1卷积层
        self.p4_1 = nn.MaxPool2d(kernel_size=3, stride=1, padding=1)
        self.p4_2 = nn.Conv2d(in_channels, c4, kernel_size=1)

    def forward(self, x):
        p1 = F.relu(self.p1_1(x))
        p2 = F.relu(self.p2_2(F.relu(self.p2_1(x))))
        p3 = F.relu(self.p3_2(F.relu(self.p3_1(x))))
        p4 = F.relu(self.p4_2(self.p4_1(x)))
        # 在通道维度上连结输出
        return torch.cat((p1, p2, p3, p4), dim=1)

那么为什么 GoogLeNet 这个网络如此有效呢？首先我们考虑一下滤波器（filter）的组合，它们可以用各种滤波器尺寸探索图像，这意味着不同大小的滤波器可以有效地识别不同范围的图像细节。同时，我们可以为不同的滤波器分配不同数量的参数。

4.2 GoogLeNet模型

如下图所示，GoogLeNet 一共使用 $9$ 个 Inception 块和全局平均汇聚层的堆叠来生成其估计值。Inception 块之间的最大汇聚层可降低维度。第一个模块类似于 AlexNet 和 LeNet，Inception 块的组合从 VGG 继承，全局平均汇聚层避免了在最后使用全连接层。

GoogLeNet架构。

现在，我们逐一实现 GoogLeNet 的每个模块。第一个模块使用 $64$ 个通道、$7\times 7$ 卷积层。

b1 = nn.Sequential(nn.Conv2d(1, 64, kernel_size=7, stride=2, padding=3),
                   nn.ReLU(),
                   nn.MaxPool2d(kernel_size=3, stride=2, padding=1))

第二个模块使用两个卷积层：第一个卷积层是 $64$ 个通道、$1\times 1$ 卷积层；第二个卷积层使用将通道数量增加三倍的 $3\times 3$ 卷积层。这对应于 Inception 块中的第二条路径。

b2 = nn.Sequential(nn.Conv2d(64, 64, kernel_size=1),
                   nn.ReLU(),
                   nn.Conv2d(64, 192, kernel_size=3, padding=1),
                   nn.ReLU(),
                   nn.MaxPool2d(kernel_size=3, stride=2, padding=1))

第三个模块串联两个完整的 Inception 块。第一个 Inception 块的输出通道数为 $64+128+32+32=256$，四个路径之间的输出通道数量比为 $64:128:32:32=2:4:1:1$。 第二个和第三个路径首先将输入通道的数量分别减少到 $96/192=1/2$ 和 $16/192=1/12$，然后连接第二个卷积层。第二个Inception块的输出通道数增加到 $128+192+96+64=480$，四个路径之间的输出通道数量比为 $128:192:96:64=4:6:3:2$。第二条和第三条路径首先将输入通道的数量分别减少到 $128/256=1/2$ 和 $32/256=1/8$。

b3 = nn.Sequential(Inception(192, 64, (96, 128), (16, 32), 32),
                   Inception(256, 128, (128, 192), (32, 96), 64),
                   nn.MaxPool2d(kernel_size=3, stride=2, padding=1))

第四模块更加复杂，它串联了 $5$ 个 Inception 块，其输出通道数分别是 $192+208+48+64=512$、$160+224+64+64=512$、$128+256+64+64=512$、$112+288+64+64=528$ 和 $256+320+128+128=832$。这些路径的通道数分配和第三模块中的类似，首先是含 $3\times 3$ 卷积层的第二条路径输出最多通道，其次是仅含 $1\times 1$ 卷积层的第一条路径，之后是含 $5\times 5$ 卷积层的第三条路径和含 $3\times 3$ 最大汇聚层的第四条路径。其中第二、第三条路径都会先按比例减小通道数。这些比例在各个 Inception 块中都略有不同。

b4 = nn.Sequential(Inception(480, 192, (96, 208), (16, 48), 64),
                   Inception(512, 160, (112, 224), (24, 64), 64),
                   Inception(512, 128, (128, 256), (24, 64), 64),
                   Inception(512, 112, (144, 288), (32, 64), 64),
                   Inception(528, 256, (160, 320), (32, 128), 128),
                   nn.MaxPool2d(kernel_size=3, stride=2, padding=1))

第五模块包含输出通道数为 $256+320+128+128=832$ 和 $384+384+128+128=1024$ 的两个Inception块。其中每条路径通道数的分配思路和第三、第四模块中的一致，只是在具体数值上有所不同。需要注意的是，第五模块的后面紧跟输出层，该模块同 NiN 一样使用全局平均汇聚层，将每个通道的高和宽变成 $1$。最后我们将输出变成二维数组，再接上一个输出个数为标签类别数的全连接层。

b5 = nn.Sequential(Inception(832, 256, (160, 320), (32, 128), 128),
                   Inception(832, 384, (192, 384), (48, 128), 128),
                   nn.AdaptiveAvgPool2d((1,1)),
                   nn.Flatten())

net = nn.Sequential(b1, b2, b3, b4, b5, nn.Linear(1024, 10))

GoogLeNet 模型的计算复杂，而且不如 VGG 那样便于修改通道数。为了使 Fashion-MNIST 上的训练短小精悍，我们将输入的高和宽从 $224$ 降到 $96$，这简化了计算。下面演示各个模块输出的形状变化。

X = torch.rand(size=(1, 1, 96, 96))
for layer in net:
    X = layer(X)
    print(layer.__class__.__name__,'output shape:\t', X.shape)

Sequential output shape: torch.Size([1, 64, 24, 24])
Sequential output shape: torch.Size([1, 192, 12, 12])
Sequential output shape: torch.Size([1, 480, 6, 6])
Sequential output shape: torch.Size([1, 832, 3, 3])
Sequential output shape: torch.Size([1, 1024])
Linear output shape: torch.Size([1, 10])

4.3 训练模型

和以前一样，我们使用 Fashion-MNIST 数据集来训练我们的模型。在训练之前，我们将图片转换为 $96\times 96$ 分辨率。

lr, num_epochs, batch_size = 0.1, 10, 128
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size, resize=96)
d2l.train_ch6(net, train_iter, test_iter, num_epochs, lr, d2l.try_gpu())

loss 0.254, train acc 0.904, test acc 0.885
3570.5 examples/sec on cuda:0

4.4 小结

• Inception块相当于一个有 $4$ 条路径的子网络。它通过不同窗口形状的卷积层和最大汇聚层来并行抽取信息，并使用 $1\times 1$ 卷积层减少每像素级别上的通道维数从而降低模型复杂度。
• GoogLeNet 将多个设计精细的 Inception 块与其他层（卷积层、全连接层）串联起来。其中 Inception 块的通道数分配之比是在ImageNet数据集上通过大量的实验得来的。
• GoogLeNet 和它的后继者们一度是 ImageNet 上最有效的模型之一：它以较低的计算复杂度提供了类似的测试精度。

5. 批量规范化

训练深层神经网络是十分困难的，特别是在较短的时间内使他们收敛更加棘手。在本节中，我们将介绍批量规范化(batch normalization)[Ioffe & Szegedy, 2015]，这是一种流行且有效的技术，可持续加速深层网络的收敛速度。再结合在下一节节中将介绍的残差块，批量规范化使得研究人员能够训练 $100$ 层以上的网络。

5.1 训练深层网络

为什么需要批量规范化层呢？让我们来回顾一下训练神经网络时出现的一些实际挑战。

首先，数据预处理的方式通常会对最终结果产生巨大影响。回想一下我们应用多层感知机来预测房价的例子。 使用真实数据时，我们的第一步是标准化输入特征，使其平均值为 $0$，方差为 $1$。直观地说，这种标准化可以很好地与我们的优化器配合使用，因为它可以将参数的量级进行统一。

第二，对于典型的多层感知机或卷积神经网络。当我们训练时，中间层中的变量（例如，多层感知机中的仿射变换输出）可能具有更广的变化范围：不论是沿着从输入到输出的层，跨同一层中的单元，或是随着时间的推移，模型参数的随着训练更新变幻莫测。批量规范化的发明者非正式地假设，这些变量分布中的这种偏移可能会阻碍网络的收敛。直观地说，我们可能会猜想，如果一个层的可变值是另一层的 $100$ 倍，这可能需要对学习率进行补偿调整。

第三，更深层的网络很复杂，容易过拟合。这意味着正则化变得更加重要。

批量规范化应用于单个可选层（也可以应用到所有层），其原理如下：在每次训练迭代中，我们首先规范化输入，即通过减去其均值并除以其标准差，其中两者均基于当前小批量处理。接下来，我们应用比例系数和比例偏移。正是由于这个基于批量统计的标准化，才有了批量规范化的名称。

请注意，如果我们尝试使用大小为 $1$ 的小批量应用批量规范化，我们将无法学到任何东西。这是因为在减去均值之后(减去我自己？)，每个隐藏单元将为 $0$。所以，只有使用足够大的小批量，批量规范化这种方法才是有效且稳定的。请注意，在应用批量规范化时，批量大小的选择可能比没有批量规范化时更重要。

从形式上来说，用 $\mathbf{x}\in \mathcal{B}$ 表示一个来自小批量 $\mathcal{B}$ 的输入，批量规范化 $\mathrm{BN}$ 根据以下表达式转换 $\mathbf{x}$ :
$$\mathrm{BN}(\mathbf{x})=\mathbf{\gamma }\odot \frac{\mathbf{x}-{\hat{\mathbf{\mu }}}_{\mathcal{B}}}{{\hat{\mathbf{\sigma }}}_{\mathcal{B}}}+\mathbf{\beta }.$$

批量的 平均值为$0$ 和 单位方差为$1$ 。由于单位方差（与其他一些魔法数）是一个主观的选择，因此我们通常包含 拉伸参数 (scale) $\gamma$ 和 偏移参数 (shift) $\beta$，它们的形状与 $\mathbf{x}$ 相同。请注意，$\gamma$ 和 $\beta$ 是需要与其他模型参数一起学习的参数。

由于在训练过程中，中间层的变化幅度不能过于剧烈，而批量规范化将每一层主动居中，并将它们重新调整为给定的平均值和大小（通过 ${\hat{\mathbf{\mu }}}_{\mathcal{B}}$ 和 ${\hat{\mathbf{\sigma }}}_{\mathcal{B}}）$ 。

从形式上来看，我们计算出 $\mathrm{BN}(\mathbf{x})=\mathbf{\gamma }\odot \frac{\mathbf{x}-{\hat{\mathbf{\mu }}}_{\mathcal{B}}}{{\hat{\mathbf{\sigma }}}_{\mathcal{B}}}+\mathbf{\beta }$ 中的 ${\hat{\mathbf{\mu }}}_{\mathcal{B}}$ 和 ${\hat{\sigma }}_{\mathcal{B}}$，如下所示(这里的意思是，求$\mathbf{x}$内的每一个特征分量的平均值吧？)：
$$\begin{array}{rl}{\hat{\mathbf{\mu }}}_{\mathcal{B}}& =\frac{1}{|\mathcal{B}|}\sum _{\mathbf{x}\in \mathcal{B}}\mathbf{x},\\ {\hat{\mathbf{\sigma }}}_{\mathcal{B}}^2& =\frac{1}{|\mathcal{B}|}\sum _{\mathbf{x}\in \mathcal{B}}{\left(\mathbf{x}-{\hat{\mathbf{\mu }}}_{\mathcal{B}}\right)}^2+ϵ.\end{array}$$

请注意，我们在方差估计值中添加一个小的常量 $ϵ>0$，以确保我们永远不会尝试除以零，即使在经验方差估计值可能消失的情况下也是如此。估计值 ${\hat{\mathbf{\mu }}}_{\mathcal{B}}$ 和 ${\hat{\sigma }}_{\mathcal{B}}$ 通过使用平均值和方差的噪声 (noise)估计来抵消缩放问题。你可能会认为这种噪声是一个问题，而事实上它是有益的。

事实证明，这是深度学习中一个反复出现的主题。由于尚未在理论上明确的原因(尚未在理论上明确原因还行)，优化中的各种噪声源通常会导致更快的训练和较少的过拟合：这种变化似乎是正则化的一种形式。在一些初步研究中，[Teye et al., 2018] 和 [Luo et al., 2018] 分别将批量规范化的性质与贝叶斯先验相关联。这些理论揭示了为什么批量规范化最适应 $50\sim 100$ 范围中的中等批量大小的难题。

另外，批量规范化层在”训练模式“（通过小批量统计数据规范化）和“预测模式”（通过数据集统计规范化）中的功能不同。在训练过程中，我们无法得知使用整个数据集来估计平均值和方差，所以只能根据每个小批次的平均值和方差不断训练模型。而在预测模式下，可以根据整个数据集精确计算批量规范化所需的平均值和方差。

现在，我们了解一下批量规范化在实践中是如何工作的。

5.2 批量规范化层

回想一下，批量规范化和其他层之间的一个关键区别是，由于批量规范化在完整的小批量上运行，因此我们不能像以前在引入其他层时那样忽略批量大小。 我们在下面讨论这两种情况：全连接层和卷积层，他们的批量规范化实现略有不同。

5.2.1 全连接层

通常，我们将批量规范化层置于全连接层中的仿射变换和激活函数之间。设全连接层的输入为 $\mathbf{x}$，权重参数和偏置参数分别为 $\mathbf{W}$ 和 $\mathbf{b}$，激活函数为 $\varphi$，批量规范化的运算符为 $\mathrm{BN}$。 那么，使用批量规范化的全连接层的输出的计算详情如下(这里的公式只说明了顺序如下：仿射->BN->激活)：
$$\mathbf{h}=\varphi (\mathrm{BN}(\mathbf{Wx}+\mathbf{b}))$$

回想一下，均值和方差是在应用变换的”相同”小批量上计算的。

5.2.2 卷积层

同样，对于卷积层，我们可以在卷积层之后和非线性激活函数之前应用批量规范化。当卷积有多个输出通道时，我们需要对这些通道的“每个”输出执行批量规范化，每个通道都有自己的拉伸（scale）和偏移（shift）参数，这两个参数都是标量。假设我们的小批量包含 $m$ 个样本，并且对于每个通道，卷积的输出具有高度 $p$ 和宽度 $q$。那么对于卷积层，我们在每个输出通道的 $m\cdot p\cdot q$ 个元素上同时执行每个批量规范化。因此，在计算平均值和方差时，我们会收集所有空间位置的值，然后在给定通道内应用相同的均值和方差，以便在每个空间位置对值进行规范化(这里很重要！是对每个通道求了一个均值做 BN)。

5.2.3 预测过程中的批量规范化

正如我们前面提到的，批量规范化在训练模式和预测模式下的行为通常不同。首先，将训练好的模型用于预测时，我们不再需要样本均值中的噪声以及在微批次上估计每个小批次产生的样本方差了。其次，例如，我们可能需要使用我们的模型对逐个样本进行预测。一种常用的方法是通过移动平均估算整个训练数据集的样本均值和方差，并在预测时使用它们得到确定的输出。可见，和暂退法一样，批量规范化层在训练模式和预测模式下的计算结果也是不一样的。

5.3 从零实现

下面，我们从头开始实现一个具有张量的批量规范化层。

import torch
from torch import nn
from d2l import torch as d2l


def batch_norm(X, gamma, beta, moving_mean, moving_var, eps, momentum):
    # 通过is_grad_enabled来判断当前模式是训练模式还是预测模式
    if not torch.is_grad_enabled():
        # 如果是在预测模式下，直接使用传入的移动平均所得的均值和方差
        X_hat = (X - moving_mean) / torch.sqrt(moving_var + eps)
    else:
        assert len(X.shape) in (2, 4)
        if len(X.shape) == 2:
            # 使用全连接层的情况，计算特征维上的均值和方差
            mean = X.mean(dim=0)
            var = ((X - mean) ** 2).mean(dim=0)
        else:
            # 使用二维卷积层的情况，计算通道维上（axis=1）的均值和方差。## 在channel通道计算
            # 这里我们需要保持X的形状以便后面可以做广播运算
            mean = X.mean(dim=(0, 2, 3), keepdim=True)
            var = ((X - mean) ** 2).mean(dim=(0, 2, 3), keepdim=True)
        # 训练模式下，用当前的均值和方差做标准化
        X_hat = (X - mean) / torch.sqrt(var + eps)
        # 更新移动平均的均值和方差
        moving_mean = momentum * moving_mean + (1.0 - momentum) * mean
        moving_var = momentum * moving_var + (1.0 - momentum) * var
    Y = gamma * X_hat + beta  # 缩放和移位
    return Y, moving_mean.data, moving_var.data

我们现在可以创建一个正确的BatchNorm层。这个层将保持适当的参数：拉伸gamma和偏移beta，这两个参数将在训练过程中更新。此外，我们的层将保存均值和方差的移动平均值，以便在模型预测期间随后使用。

撇开算法细节，注意我们实现层的基础设计模式。通常情况下，我们用一个单独的函数定义其数学原理，比如说batch_norm。然后，我们将此功能集成到一个自定义层中，其代码主要处理数据移动到训练设备（如GPU）、分配和初始化任何必需的变量、跟踪移动平均线（此处为均值和方差）等问题。为了方便起见，我们并不担心在这里自动推断输入形状，因此我们需要指定整个特征的数量。不用担心，深度学习框架中的批量规范化API将为我们解决上述问题，我们稍后将展示这一点。

class BatchNorm(nn.Module):
    # num_features：完全连接层的输出数量或卷积层的输出通道数。
    # num_dims：2表示完全连接层，4表示卷积层
    def __init__(self, num_features, num_dims):
        super().__init__()
        if num_dims == 2:
            shape = (1, num_features)
        else:
            shape = (1, num_features, 1, 1)
        # 参与求梯度和迭代的拉伸和偏移参数，分别初始化成1和0
        self.gamma = nn.Parameter(torch.ones(shape))
        self.beta = nn.Parameter(torch.zeros(shape))
        # 非模型参数的变量初始化为0和1
        self.moving_mean = torch.zeros(shape)
        self.moving_var = torch.ones(shape)

    def forward(self, X):
        # 如果X不在内存上，将moving_mean和moving_var
        # 复制到X所在显存上
        if self.moving_mean.device != X.device:
            self.moving_mean = self.moving_mean.to(X.device)
            self.moving_var = self.moving_var.to(X.device)
        # 保存更新过的moving_mean和moving_var
        Y, self.moving_mean, self.moving_var = batch_norm(
            X, self.gamma, self.beta, self.moving_mean,
            self.moving_var, eps=1e-5, momentum=0.9)
        return Y

5.4 使用批量规范化层的 LeNet

为了更好理解如何应用 BatchNorm，下面我们将其应用于 LeNet 模型。回想一下，批量规范化是在卷积层或全连接层之后、相应的激活函数之前应用的。

net = nn.Sequential(
    nn.Conv2d(1, 6, kernel_size=5), BatchNorm(6, num_dims=4), nn.Sigmoid(),
    nn.AvgPool2d(kernel_size=2, stride=2),
    nn.Conv2d(6, 16, kernel_size=5), BatchNorm(16, num_dims=4), nn.Sigmoid(),
    nn.AvgPool2d(kernel_size=2, stride=2), nn.Flatten(),
    nn.Linear(16*4*4, 120), BatchNorm(120, num_dims=2), nn.Sigmoid(),
    nn.Linear(120, 84), BatchNorm(84, num_dims=2), nn.Sigmoid(),
    nn.Linear(84, 10))

和以前一样，我们将在 Fashion-MNIST 数据集上训练网络。这个代码与我们第一次训练 LeNet 时几乎完全相同，主要区别在于学习率大得多。

lr, num_epochs, batch_size = 1.0, 10, 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)
d2l.train_ch6(net, train_iter, test_iter, num_epochs, lr, d2l.try_gpu())

loss 0.268, train acc 0.900, test acc 0.831
38739.6 examples/sec on cuda:0

让我们来看看从第一个批量规范化层中学到的 拉伸参数gamma 和 偏移参数beta。

net[1].gamma.reshape((-1,)), net[1].beta.reshape((-1,))

(tensor([0.3362, 4.0349, 0.4496, 3.7056, 3.7774, 2.6762], device=‘cuda:0’, grad_fn=),
tensor([-0.5739, 4.1376, 0.5126, 0.3060, -2.5187, 0.3683], device=‘cuda:0’, grad_fn=))

5.5 简明实现

除了使用我们刚刚定义的 BatchNorm，我们也可以直接使用深度学习框架中定义的 BatchNorm。该代码看起来几乎与我们上面的代码相同。

net = nn.Sequential(
    nn.Conv2d(1, 6, kernel_size=5), nn.BatchNorm2d(6), nn.Sigmoid(),
    nn.AvgPool2d(kernel_size=2, stride=2),
    nn.Conv2d(6, 16, kernel_size=5), nn.BatchNorm2d(16), nn.Sigmoid(),
    nn.AvgPool2d(kernel_size=2, stride=2), nn.Flatten(),
    nn.Linear(256, 120), nn.BatchNorm1d(120), nn.Sigmoid(),
    nn.Linear(120, 84), nn.BatchNorm1d(84), nn.Sigmoid(),
    nn.Linear(84, 10))

下面，我们使用相同超参数来训练模型。请注意，通常高级API变体运行速度快得多，因为它的代码已编译为 C++ 或CUDA，而我们的自定义代码由 Python 实现。

d2l.train_ch6(net, train_iter, test_iter, num_epochs, lr, d2l.try_gpu())

loss 0.269, train acc 0.901, test acc 0.853
64557.2 examples/sec on cuda:0

5.6 争议

直观地说，批量规范化被认为可以使优化更加平滑。然而，我们必须小心区分直觉和对我们观察到的现象的真实解释。回想一下，我们甚至不知道简单的神经网络（多层感知机和传统的卷积神经网络）为什么如此有效。即使在暂退法和权重衰减的情况下，它们仍然非常灵活，因此无法通过常规的学习理论泛化保证来解释它们是否能够泛化到看不见的数据。

在提出批量规范化的论文中，作者除了介绍了其应用，还解释了其原理：通过减少内部协变量偏移（internal covariate shift）。据推测，作者所说的“内部协变量转移”类似于上述的投机直觉，即变量值的分布在训练过程中会发生变化。 然而，这种解释有两个问题：
1、这种偏移与严格定义的协变量偏移（covariate shift）非常不同，所以这个名字用词不当。
2、这种解释只提供了一种不明确的直觉，但留下了一个有待后续挖掘的问题：为什么这项技术如此有效？本书旨在传达实践者用来发展深层神经网络的直觉。然而，重要的是将这些指导性直觉与既定的科学事实区分开来。最终，当你掌握了这些方法，并开始撰写自己的研究论文时，你会希望清楚地区分技术和直觉。

随着批量规范化的普及，“内部协变量偏移”的解释反复出现在技术文献的辩论，特别是关于“如何展示机器学习研究”的更广泛的讨论中。Ali Rahimi在接受2017年NeurIPS大会的“接受时间考验奖”（Test of Time Award）时发表了一篇令人难忘的演讲。他将“内部协变量转移”作为焦点，将现代深度学习的实践比作炼金术。他对该示例进行了详细回顾 [Lipton & Steinhardt, 2018]，概述了机器学习中令人不安的趋势。此外，一些作者对批量规范化的成功提出了另一种解释：在某些方面，批量规范化的表现出与原始论文 [Santurkar et al., 2018]中声称的行为是相反的。

然而，与机器学习文献中成千上万类似模糊的说法相比，内部协变量偏移没有更值得批评。很可能，它作为这些辩论的焦点而产生共鸣，要归功于目标受众对它的广泛认可。批量规范化已经被证明是一种不可或缺的方法。它适用于几乎所有图像分类器，并在学术界获得了数万引用。

5.7 小结

• 在模型训练过程中，批量规范化利用小批量的均值和标准差，不断调整神经网络的中间输出，使整个神经网络各层的中间输出值更加稳定。
• 批量规范化在全连接层和卷积层的使用略有不同。
• 批量规范化层和暂退层一样，在训练模式和预测模式下计算不同。
• 批量规范化有许多有益的副作用，主要是正则化。另一方面，”减少内部协变量偏移“的原始动机似乎不是一个有效的解释。

6. 残差网络（ResNet）

随着我们设计越来越深的网络，深刻理解“新添加的层如何提升神经网络的性能”变得至关重要。更重要的是设计网络的能力，在这种网络中，添加层会使网络更具表现力，为了取得质的突破，我们需要一些数学基础知识。(更深层的网络性能不一定会更好，实验发现深度网络中出现了退化问题(Degradation problem)：网络深度增加时，网络准确度出现饱和，甚至出现下降，如下图所示。这不会是过拟合问题，因为56层网络的训练误差同样高。我们知道深层网络存在着梯度消失或者爆炸的问题，这使得深度学习模型很难训练。)

20层与56层网络在CIFAR-10上的误差。

6.1 函数类

首先，假设有一类特定的神经网络架构 $\mathcal{F}$，它包括学习速率和其他超参数设置(训练前设置的)。对于所有 $f\in \mathcal{F}$，存在一些参数集（例如权重和偏置），这些参数可以通过在合适的数据集上进行训练而获得(训练时得到的)。现在假设 $f^{\ast }$ 是我们真正想要找到的函数，如果是 $f^{\ast }\in \mathcal{F}$，那我们可以轻而易举的训练得到它，但通常我们不会那么幸运。相反，我们将尝试找到一个函数 $f_{\mathcal{F}}^{\ast }$，这是我们在 $\mathcal{F}$ 中的最佳选择。例如，给定一个具有 $\mathbf{X}$ 特性和 $\mathbf{y}$ 标签的数据集，我们可以尝试通过解决以下优化问题来找到它：
$$f_{\mathcal{F}}^{\ast }:=\underset{f}{\mathrm{argmin}}L(\mathbf{X},\mathbf{y},f)\text{ subject to }f\in \mathcal{F}.$$

那么，怎样得到更近似真正 $f^{\ast }$ 的函数呢? 唯一合理的可能性是，我们需要设计一个更强大的架构 ${\mathcal{F}}^{\prime }$ 。换句话说，我们预计 $f_{{\mathcal{F}}^{\prime }}^{\ast }$，比 $f_{\mathcal{F}}^{\ast }$ “更近似”。然而，如果 $\mathcal{F}⊈{\mathcal{F}}^{\prime }$，则无法保证新的体系“更近似”。事实上，$f_{{\mathcal{F}}^{\prime }}^{\ast }$ 可能更糟：如下图所示，对于非嵌套函数 (non-nested function) 类，较复杂的函数类并不总是向“真”函数 $f^{\ast }$ 靠拢（复杂度由 ${\mathcal{F}}_1$ 向 ${\mathcal{F}}_6$ 递增）。在下图的左边，虽然 ${\mathcal{F}}_3$ 比 ${\mathcal{F}}_1$ 更接近 $f^{\ast }$, 但 ${\mathcal{F}}_6$ 却离的更远了。相反对于下图右侧的嵌套函数 (nested function) 类 ${\mathcal{F}}_1\subseteq \dots \subseteq {\mathcal{F}}_6$，我们可以避免上述问题。

对于非嵌套函数类，较复杂（由较大区域表示）的函数类不能保证更接近“真”函数（ $f^{\ast }$）。这种现象在嵌套函数类中不会发生。

因此，只有当较复杂的函数类包含较小的函数类(嵌套函数)时，我们才能确保提高它们的性能。对于深度神经网络，如果我们能将新添加的层训练成恒等映射（identity function）$f(\mathbf{x})=\mathbf{x}$，新模型和原模型将同样有效(现在你有一个浅层网络，你想通过向上堆积新层来建立深层网络，一个极端情况是这些增加的层什么也不学习，仅仅复制浅层网络的特征，即这样新层是恒等映射。在这种情况下，深层网络应该至少和浅层网络性能一样，也不应该出现退化现象。)。同时，由于新模型可能得出更优的解来拟合训练数据集，因此添加层似乎更容易降低训练误差。

针对这一问题，何恺明等人提出了残差网络（ResNet） [He et al., 2016a]。它在2015年的 ImageNet 图像识别挑战赛夺魁，并深刻影响了后来的深度神经网络的设计。残差网络的核心思想是：每个附加层都应该更容易地包含原始函数作为其元素之一。于是，残差块（residual blocks）便诞生了，这个设计对如何建立深层神经网络产生了深远的影响。凭借它，ResNet 赢得了 2015 年 ImageNet 大规模视觉识别挑战赛。

6.2 残差块

让我们聚焦于神经网络局部：下图所示，假设我们的原始输入为 $\mathbf{x}$，而希望学出的理想映射为 $f(\mathbf{x})$（作为下图上方激活函数的输入）。下图左边虚线框中的部分需要直接拟合出该映射 $f(\mathbf{x})$，而右图虚线框中的部分则需要拟合出残差映射 $f(\mathbf{x})=\mathbf{x}$(也就是最小化$f(\mathbf{x})-\mathbf{x}$，使其近似0)。 残差映射在现实中往往更容易优化。以本节开头提到的恒等映射作为我们希望学出的理想映射 $f(\mathbf{x})$，我们只需将下图右边虚线框内上方的加权运算（如仿射）的权重和偏置参数设成 $0$，那么 $f(\mathbf{x})$ 即为恒等映射。实际中，当理想映射 $f(\mathbf{x})$ 极接近于恒等映射时，残差映射也易于捕捉恒等映射的细微波动。下图右边是 ResNet 的基础架构—–残差块（residual block）。在残差块中，输入可通过跨层数据线路更快地向前传播。

一个正常块（左图）和一个残差块（右图）。

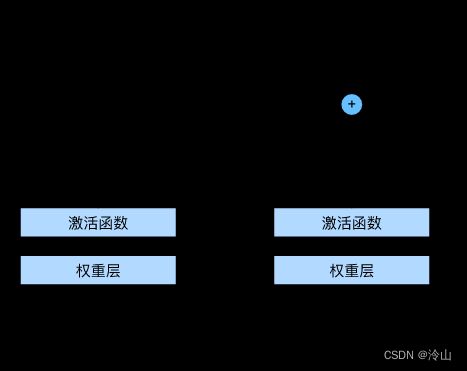
ResNet 沿用了 VGG 完整的 $3\times 3$ 卷积层设计。残差块里首先有 $2$ 个有相同输出通道数的 $3\times 3$ 卷积层(注意是$2$个)。每个卷积层后接一个批量规范化层和 ReLU 激活函数。然后我们通过跨层数据通路，跳过这 $2$ 个卷积运算，将输入直接加在最后的 ReLU 激活函数前(注意是在第$2$个ReLU前)。这样的设计要求 $2$ 个卷积层的输出与输入形状一样，从而使它们可以相加。如果想改变通道数，就需要引入一个额外的 $1\times 1$ 卷积层来将输入变换成需要的形状后再做相加运算。残差块的实现如下：

import torch
from torch import nn
from torch.nn import functional as F
from d2l import torch as d2l


class Residual(nn.Module):  #@save
    def __init__(self, input_channels, num_channels,
                 use_1x1conv=False, strides=1):
        super().__init__()
        self.conv1 = nn.Conv2d(input_channels, num_channels,
                               kernel_size=3, padding=1, stride=strides)
        self.conv2 = nn.Conv2d(num_channels, num_channels,
                               kernel_size=3, padding=1)
        if use_1x1conv:
            self.conv3 = nn.Conv2d(input_channels, num_channels,
                                   kernel_size=1, stride=strides)
        else:
            self.conv3 = None
        self.bn1 = nn.BatchNorm2d(num_channels)
        self.bn2 = nn.BatchNorm2d(num_channels)

    def forward(self, X):
        Y = F.relu(self.bn1(self.conv1(X))) ##卷积->bn->relu
        Y = self.bn2(self.conv2(Y)) ##卷积->bn
        if self.conv3: ##如果需要1*1卷积
            X = self.conv3(X)
        Y += X ##加上原始输入
        return F.relu(Y)

如下图所示，此代码生成两种类型的网络： 一种是当 use_1x1conv=False 时，应用 ReLU 非线性函数之前，将输入添加到输出。 另一种是当 use_1x1conv=True 时，添加通过 $1\times 1$ 卷积调整通道和分辨率(通过调整步长降低分辨率)。

包含以及不包含 $1\times 1$ 卷积层的残差块。

下面我们来查看输入和输出形状一致的情况。

blk = Residual(3,3)
X = torch.rand(4, 3, 6, 6)
Y = blk(X)
Y.shape

torch.Size([4, 3, 6, 6])

我们也可以在增加输出通道数的同时，减半输出的高和宽。

blk = Residual(3,6, use_1x1conv=True, strides=2)
blk(X).shape

torch.Size([4, 6, 3, 3])

6.3 ResNet模型

ResNet 的前两层跟之前介绍的 GoogLeNet 中的一样：在输出通道数为 $64$、步幅为 $2$ 的卷积层后，接步幅为 $2$ 的 $7\times 7$ 的最大汇聚层。不同之处在于 ResNet 每个卷积层后增加了批量规范化层。

b1 = nn.Sequential(nn.Conv2d(1, 64, kernel_size=7, stride=2, padding=3),
                   nn.BatchNorm2d(64), nn.ReLU(),
                   nn.MaxPool2d(kernel_size=3, stride=2, padding=1))

GoogLeNet 在后面接了 $4$ 个由 Inception 块组成的模块。ResNet 则使用 $4$ 个由残差块组成的模块，每个模块使用若干个同样输出通道数的残差块。第一个模块的通道数同输入通道数一致。由于之前已经使用了步幅为 $2$ 的最大汇聚层，所以无须减小高和宽。之后的每个模块在第一个残差块里将上一个模块的通道数翻倍，并将高和宽减半。

下面我们来实现这个模块。注意，我们对第一个模块做了特别处理。

def resnet_block(input_channels, num_channels, num_residuals,
                 first_block=False):
    blk = []
    for i in range(num_residuals):
        if i == 0 and not first_block:
            blk.append(Residual(input_channels, num_channels,
                                use_1x1conv=True, strides=2))
        else:
            blk.append(Residual(num_channels, num_channels))
    return blk

接着在 ResNet 加入所有残差块，这里每个模块使用 $2$ 个残差块。

b2 = nn.Sequential(*resnet_block(64, 64, 2, first_block=True))
b3 = nn.Sequential(*resnet_block(64, 128, 2))
b4 = nn.Sequential(*resnet_block(128, 256, 2))
b5 = nn.Sequential(*resnet_block(256, 512, 2))

最后，与 GoogLeNet 一样，在 ResNet 中加入全局平均汇聚层，以及全连接层输出。

net = nn.Sequential(b1, b2, b3, b4, b5,
                    nn.AdaptiveAvgPool2d((1,1)),
                    nn.Flatten(), nn.Linear(512, 10))

每个模块有 $4$ 个卷积层（不包括恒等映射的$1\times 1$卷积层）。加上第一个 $7\times 7$ 卷积层和最后一个全连接层，共有 $18$ 层。因此，这种模型通常被称为 ResNet-18。通过配置不同的通道数和模块里的残差块数可以得到不同的 ResNet 模型，例如更深的含 $152$ 层的 ResNet-152。虽然 ResNet 的主体架构跟 GoogLeNet 类似，但 ResNet 架构更简单，修改也更方便。这些因素都导致了 ResNet 迅速被广泛使用。下图描述了完整的 ResNet-18。

ResNet-18 架构。

在训练 ResNet 之前，让我们观察一下 ResNet 中不同模块的输入形状是如何变化的。在之前所有架构中，分辨率降低，通道数量增加，直到全局平均汇聚层聚集所有特征。

X = torch.rand(size=(1, 1, 224, 224))
for layer in net:
    X = layer(X)
    print(layer.__class__.__name__,'output shape:\t', X.shape)

Sequential output shape: torch.Size([1, 64, 56, 56])
Sequential output shape: torch.Size([1, 64, 56, 56])
Sequential output shape: torch.Size([1, 128, 28, 28])
Sequential output shape: torch.Size([1, 256, 14, 14])
Sequential output shape: torch.Size([1, 512, 7, 7])
AdaptiveAvgPool2d output shape: torch.Size([1, 512, 1, 1])
Flatten output shape: torch.Size([1, 512])
Linear output shape: torch.Size([1, 10])

6.4 训练模型

同之前一样，我们在 Fashion-MNIST 数据集上训练 ResNet。

lr, num_epochs, batch_size = 0.05, 10, 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size, resize=96)
d2l.train_ch6(net, train_iter, test_iter, num_epochs, lr, d2l.try_gpu())

loss 0.011, train acc 0.997, test acc 0.915
4701.1 examples/sec on cuda:0

6.5 小结

• 学习嵌套函数（nested function）是训练神经网络的理想情况。在深层神经网络中，学习另一层作为恒等映射（identity function）较容易（尽管这是一个极端情况）。
• 残差映射可以更容易地学习同一函数，例如将权重层中的参数近似为零。
• 利用残差块（residual blocks）可以训练出一个有效的深层神经网络：输入可以通过层间的残余连接更快地向前传播。
• 残差网络（ResNet）对随后的深层神经网络设计产生了深远影响。

6.6 补充

作者对比 18-layer 和 34-layer 的网络效果，如下图所示。可以看到普通的网络出现退化现象，但是 ResNet 很好的解决了退化问题。

18-layer和34-layer的网络效果。

7. 稠密连接网络（DenseNet）

ResNet 极大地改变了如何参数化深层网络中函数的观点。稠密连接网络（DenseNet） [Huang et al., 2017]在某种程度上是 ResNet 的逻辑扩展。让我们先从数学上了解一下。

7.1 从ResNet到DenseNet

回想一下任意函数的泰勒展开式（Taylor expansion），它把这个函数分解成越来越高阶的项。在 $x$ 接近 $0$ 时，
$$f(x)=f(0)+f^{\prime }(0)x+\frac{f^{\prime \prime }(0)}{2!}{x}^2+\frac{f^{\prime \prime \prime }(0)}{3!}{x}^3+\dots$$

同样，ResNet 将函数展开为
$$f(\mathbf{x})=\mathbf{x}+g(\mathbf{x}).$$

也就是说，ResNet 将 $f$ 分解为两部分：一个简单的线性项和一个复杂的非线性项。那么再向前拓展一步，如果我们想将 $f$ 拓展成超过两部分的信息呢? 一种方案便是 DenseNet。

ResNet（左）与 DenseNet（右）在跨层连接上的主要区别：使用相加和使用连结。

如上图所示，ResNet 和 DenseNet 的关键区别在于，DenseNet 输出是连接（用图中的[,]表示） 而不是如 ResNet 的简单相加。因此，在应用越来越复杂的函数序列后，我们执行从 $\mathbf{x}$ 到其展开式的映射：
$$\mathbf{x}\to \left[\mathbf{x},f_1(\mathbf{x}),f_2\left(\left[\mathbf{x},f_1(\mathbf{x})\right]\right),f_3\left(\left[\mathbf{x},f_1(\mathbf{x}),f_2\left(\left[\mathbf{x},f_1(\mathbf{x})\right]\right)\right]\right),\dots \right]$$

最后，将这些展开式结合到多层感知机中，再次减少特征的数量。实现起来非常简单：我们不需要添加术语，而是将它们连接起来。DenseNet 这个名字由变量之间的“稠密连接”而得来，最后一层与之前的所有层紧密相连。稠密连接如下图所示。

稠密连接。

稠密网络主要由 $2$ 部分构成：稠密块（dense block）和过渡层（transition layer）。前者定义如何连接输入和输出，而后者则控制通道数量，使其不会太复杂。

7.2 稠密块体

DenseNet 使用了 ResNet 改良版的“批量规范化、激活和卷积”架构（参见 7.6 节中的练习）。我们首先实现一下这个架构。

import torch
from torch import nn
from d2l import torch as d2l


def conv_block(input_channels, num_channels):
    return nn.Sequential(
        nn.BatchNorm2d(input_channels), nn.ReLU(),
        nn.Conv2d(input_channels, num_channels, kernel_size=3, padding=1))

一个稠密块由多个卷积块组成，每个卷积块使用相同数量的输出通道。然而，在前向传播中，我们将每个卷积块的输入和输出在通道维上连结。

class DenseBlock(nn.Module):
    def __init__(self, num_convs, input_channels, num_channels):
        super(DenseBlock, self).__init__()
        layer = []
        for i in range(num_convs):
            layer.append(conv_block(
                num_channels * i + input_channels, num_channels))
        self.net = nn.Sequential(*layer)

    def forward(self, X):
        for blk in self.net:
            Y = blk(X)
            # 连接通道维度上每个块的输入和输出
            X = torch.cat((X, Y), dim=1)
        return X

在下面的例子中，我们定义一个有 $2$ 个输出通道数为 $10$ 的 DenseBlock。使用通道数为 $3$ 的输入时，我们会得到通道数为 $3+2\times 10=23$ 的输出。卷积块的通道数控制了输出通道数相对于输入通道数的增长，因此也被称为增长率（growth rate）。

blk = DenseBlock(2, 3, 10)
X = torch.randn(4, 3, 8, 8)
Y = blk(X)
Y.shape

torch.Size([4, 23, 8, 8])

7.3 过渡层

由于每个稠密块都会带来通道数的增加，使用过多则会过于复杂化模型。而过渡层可以用来控制模型复杂度。它通过 $1\times 1$ 卷积层来减小通道数，并使用步幅为 $2$ 的平均汇聚层减半高和宽，从而进一步降低模型复杂度。

def transition_block(input_channels, num_channels):
    return nn.Sequential(
        nn.BatchNorm2d(input_channels), nn.ReLU(),
        nn.Conv2d(input_channels, num_channels, kernel_size=1),
        nn.AvgPool2d(kernel_size=2, stride=2))

对上一个例子中稠密块的输出使用通道数为 $10$ 的过渡层。 此时输出的通道数减为 $10$，高和宽均减半。

blk = transition_block(23, 10)
blk(Y).shape

torch.Size([4, 10, 4, 4])

7.4 DenseNet模型

我们来构造 DenseNet 模型。DenseNet 首先使用同 ResNet 一样的单卷积层和最大汇聚层。

b1 = nn.Sequential(
    nn.Conv2d(1, 64, kernel_size=7, stride=2, padding=3),
    nn.BatchNorm2d(64), nn.ReLU(),
    nn.MaxPool2d(kernel_size=3, stride=2, padding=1))

接下来，类似于 ResNet 使用的 $4$ 个残差块，DenseNet 使用的是 $4$ 个稠密块。与 ResNet 类似，我们可以设置每个稠密块使用多少个卷积层。这里我们设成 $4$，从而与上一节的 ResNet-18 保持一致。稠密块里的卷积层通道数（即增长率）设为 $32$，所以每个稠密块将增加 $128$ 个通道。

在每个模块之间，ResNet通过步幅为 $2$ 的残差块减小高和宽，DenseNet则使用过渡层来减半高和宽，并减半通道数。

# num_channels为当前的通道数
num_channels, growth_rate = 64, 32
num_convs_in_dense_blocks = [4, 4, 4, 4]
blks = []
for i, num_convs in enumerate(num_convs_in_dense_blocks):
    blks.append(DenseBlock(num_convs, num_channels, growth_rate))
    # 上一个稠密块的输出通道数
    num_channels += num_convs * growth_rate
    # 在稠密块之间添加一个转换层，使通道数量减半
    if i != len(num_convs_in_dense_blocks) - 1:
        blks.append(transition_block(num_channels, num_channels // 2))
        num_channels = num_channels // 2

与 ResNet 类似，最后接上全局汇聚层和全连接层来输出结果。

net = nn.Sequential(
    b1, *blks,
    nn.BatchNorm2d(num_channels), nn.ReLU(),
    nn.AdaptiveAvgPool2d((1, 1)),
    nn.Flatten(),
    nn.Linear(num_channels, 10))

7.5 训练模型

由于这里使用了比较深的网络，本节里我们将输入高和宽从 $224$ 降到 $96$ 来简化计算。

lr, num_epochs, batch_size = 0.1, 10, 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size, resize=96)
d2l.train_ch6(net, train_iter, test_iter, num_epochs, lr, d2l.try_gpu())

loss 0.140, train acc 0.950, test acc 0.838
5569.1 examples/sec on cuda:0

7.6 小结

• 在跨层连接上，不同于 ResNet 中将输入与输出相加，稠密连接网络（DenseNet）在通道维上连结输入与输出。
• DenseNet 的主要构建模块是稠密块和过渡层。
• 在构建 DenseNet 时，我们需要通过添加过渡层来控制网络的维数，从而再次减少通道的数量。