MATLAB BP神经网络的设计与优化
MATLAB BP神经网络的设计与优化
- 前言
- 一、数据集划分
- 二、网络拓扑结构确定
-
- 2.1 输入层与输出层
- 2.2 隐藏层个数与单元数
- 2.3 传递函数、学习函数与性能函数
- 三.初始权值、阈值的确定
-
- 3.1 随机给定[-1 1]
- 3.2 优化算法优化初始权值、阈值
- 四、训练参数设定
- 五、训练及训练效果评价
- 六、训练结果
- 七、传统BP训练与自适应学习率+动量学习训练对比
- 总结
前言
- BP(Back Propagation)神经网络,利用误差的反向传播进行权值阈值更新的前馈型神经网络,常用于解决拟合或者分类问题 。
关于神经网络和BP神经网络计算原理的详细说明和推导很多优秀的博主都已经做了相关工作:
- 神经网络学习 之 BP神经网络
- BP神经网络通俗教程(matlab实现方法)
- 一文搞定BP神经网络——从原理到应用(原理篇)
本文主要目的是针对自己在学习和做项目过程中应用BP神经网络的经验做一些总结。内容主要包括基于MATLAB的BP神经网络设计步骤以及相关优化方面的介绍。如果你已经大概了解完计算原理,正在为你对大小论文的内容进行探索,或许阅读本文可以加快你的进程。

一、数据集划分
为了避免模型在训练过程中出现过拟合的情况,针对自己的数据体量的不同,我们可以采用不同对方式对数据集进行划分。
-
数据集足够大时,可以采用训练集、测试集、验证集的划分方式,划分比例为:0.7 、0.15 、0.15 工具箱默认划分方式。
-
采用训练集、测试集的划分方式,一般比例为:0.8、0.2。
-
数据集少时采用留一法,进行循环交叉验证。
-
数据集少时,还可以通过一些方法实现数据集的增量,例如加入白噪声之后的数据以及旋转、缩小、放大后的图像。
二、网络拓扑结构确定
2.1 输入层与输出层
确定模型的输入与输出,例如研究x,y,z对t的影响。输入为3个,输出为1个,这里我想表达的是确定研究因素x y z的过程。很多因素可能是在仿真或者实验过程中全部可记录的数据,如果因素很多的情况下,可以考虑在进行训练前进行数据维度的降维处理例如:
- 机器学习中的线性映射和非线性映射方法两大方法。
- 线性映射:PCA 、LAD
- 非线性映射: 核方法(核+线性),二维化和张量化(二维+线性),流形学习(ISOMap,LLE,LPP)
2.2 隐藏层个数与单元数
(1)隐藏层个数的确定
在很多地方我们都可以看到这样一句话:
- 三层的BP神经网络可以以任意精度逼近一个任意给定的连续函数
当然这么多年的应试教育经历告诉我,要相信它。所以一般我都先用3层的进行仿真实验,实在不行最后再选择更改层数。
(2)隐藏层单元个数的确定
有两个方法:
- 给定大致范围,循环单元个数,以训练效果作为判断条件
- 参考现有文献中的经验公式确定单元个数,例如:
n=log2(输入单元数);
n=sqrt(输入单元数+输出神经元数)+a (a为[0,10]之间的常数)。
这里第二个经验公式可以结合方法1进行使用
这里,我想说两个地方。一个是对于隐藏层个数与单元数理论上来说都可以简单粗暴的使用循环来进行选择,当然前提是训练集的划分一致并且你的时间够,当然涉及到初始阈值和权值对网络的影响这个过程就变得相对复杂了很多。这也是我想说的第二点,能否考虑将初始阈值和权值对具体网络训练的影响进行某种简化的定量分析?这样一来,或许就可以使用优化算法对整个拓扑结构进行优化分析。当然这个只是我自己的瞎想,它实现的可行性和复杂性还真不好说。
2.3 传递函数、学习函数与性能函数
| 函数 | 函数名称 | 用途 |
|---|---|---|
| 传递函数 | logsig | S型对数函数 |
| 传递函数 | dlogsig | S型对数函数的导数 |
| 传递函数 | tansig | S型正切函数 |
| 传递函数 | dtansig | S型正切函数的导数 |
| 传递函数 | purelin | 纯线性函数 |
| 传递函数 | dpurelin | 纯线性函数的导数 |
| 学习函数 | learngd | 基于梯度下降法的学习函数 |
| 学习函数 | learngdm | 梯度下降动量学习函数 |
| 性能函数 | mes | 均方误差函数 |
| 性能函数 | mesreg | 均方误差规范化函数 |
三.初始权值、阈值的确定
3.1 随机给定[-1 1]
matlab工具箱中,默认初始值给定为[-1 1]之间对初始权值阈值进行随机给定。
3.2 优化算法优化初始权值、阈值
现在常见论文中,在确定好神经网络对拓扑结构后,对初始权值、阈值进行优化后再进行训练。让训练的起点相对较好,这里常用到:
- GA-BP
- PSO-BP
- GSO-BP
- ACO-BP
- BFO-BP
- ABC-BP
同时也是论文做算法比较常见的地方,当然这里的优化算法可以使用各种群智能算法,甚至改进优化算法来对BP神经网络的初值进行优化选择。这个方法很不错,可以用来快速搭建论文。关键在如何根据阈值和权值来复现这个网络,从而实现优化算法正确的适应度函数。
四、训练参数设定
训练模型的参数设定影响着训练效果,要针对不同的模型进行相关的调整。
| 项目 | 函数 |
|---|---|
| 最大迭代次数 | net.trainParam.epochs |
| 训练目标 | net.trainParam.goal |
| 训练时间 | net.trainParam.time |
| 最小梯度性能 | net.trainParam.min_grad |
| 最大确认失败次数 | net.trainParam.max_fail |
| 所用线性搜索路径 | net.trainParam.searchFcn |
| 学习率 | net.trainParam.lr |
| 动量因子 | net.trainParam.mc |
五、训练及训练效果评价
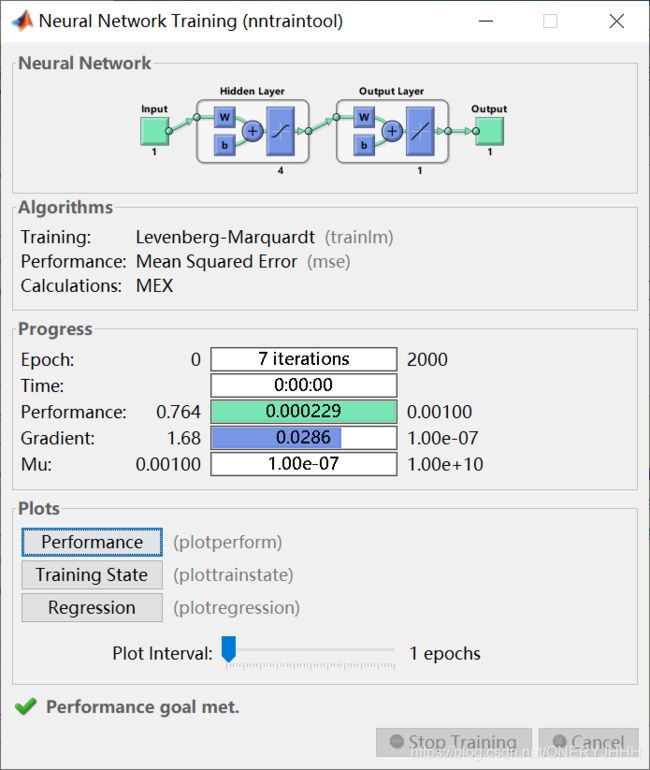
利用train函数对网络进行训练之后,可以在工具箱自带的界面中查看训练过程和训练结果。

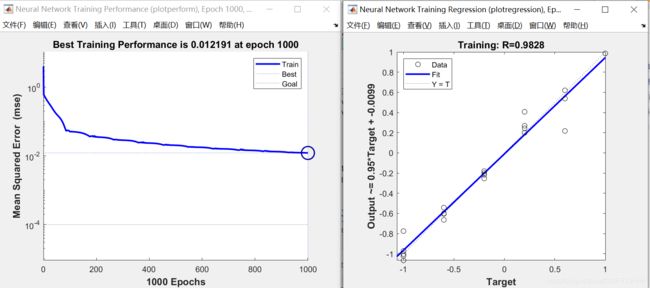
关于这里的Regression图我看到知乎和百度上都有人问,横纵坐标其实就是归一化之后的真实值和预测值,表征回归的效果。
当然为了更加方便判断模型训练完的预测效果,可以使用R2(决定系数(coefficient ofdetermination),有的教材上翻译为判定系数,也称为拟合优度。)评价预测数据和实际数据之间的相关程度。方便用来做程序的循环终止条件。
这里我之前有记录自己使用的R2计算公式以及在csdn上看到的一篇博客,可以作为参考:
- MATLAB 计算 确定系数R2
%y1为预测值 y为实际值
R2=1 - (sum((y1- y).^2) / sum((y - mean(y)).^2))
- 基于MATLAB的R方计算
function [r2 rmse] = rsquare(y,f,varargin)
% Compute coefficient of determination of data fit model and RMSE
%
% [r2 rmse] = rsquare(y,f)
% [r2 rmse] = rsquare(y,f,c)
%
% RSQUARE computes the coefficient of determination (R-square) value from
% actual data Y and model data F. The code uses a general version of
% R-square, based on comparing the variability of the estimation errors
% with the variability of the original values. RSQUARE also outputs the
% root mean squared error (RMSE) for the user's convenience.
%
% Note: RSQUARE ignores comparisons involving NaN values.
%
% INPUTS
% Y : Actual data
% F : Model fit
%
% OPTION
% C : Constant term in model
% R-square may be a questionable measure of fit when no
% constant term is included in the model.
% [DEFAULT] TRUE : Use traditional R-square computation
% FALSE : Uses alternate R-square computation for model
% without constant term [R2 = 1 - NORM(Y-F)/NORM(Y)]
%
% OUTPUT
% R2 : Coefficient of determination
% RMSE : Root mean squared error
%
% EXAMPLE
% x = 0:0.1:10;
% y = 2.*x + 1 + randn(size(x));
% p = polyfit(x,y,1);
% f = polyval(p,x);
% [r2 rmse] = rsquare(y,f);
% figure; plot(x,y,'b-');
% hold on; plot(x,f,'r-');
% title(strcat(['R2 = ' num2str(r2) '; RMSE = ' num2str(rmse)]))
%
% Jered R Wells
% 11/17/11
% jered [dot] wells [at] duke [dot] edu
%
% v1.2 (02/14/2012)
%
% Thanks to John D'Errico for useful comments and insight which has helped
% to improve this code. His code POLYFITN was consulted in the inclusion of
% the C-option (REF. File ID: #34765).
if isempty(varargin); c = true;
elseif length(varargin)>1; error 'Too many input arguments';
elseif ~islogical(varargin{1}); error 'C must be logical (TRUE||FALSE)'
else c = varargin{1};
end
% Compare inputs
if ~all(size(y)==size(f)); error 'Y and F must be the same size'; end
% Check for NaN
tmp = ~or(isnan(y),isnan(f));
y = y(tmp);
f = f(tmp);
if c; r2 = max(0,1 - sum((y(:)-f(:)).^2)/sum((y(:)-mean(y(:))).^2));
else r2 = 1 - sum((y(:)-f(:)).^2)/sum((y(:)).^2);
if r2<0
% http://web.maths.unsw.edu.au/~adelle/Garvan/Assays/GoodnessOfFit.html
warning('Consider adding a constant term to your model') %#ok<WNTAG>
r2 = 0;
end
end
rmse = sqrt(mean((y(:) - f(:)).^2));
六、训练结果
通过训练集模型的训练,测试集模型的检验,我们认为当前的模型以及可用了,可以完成数值预测以及分类预测任务。
当然,如果你需要有模型复现这个过程的话,记住要保存好对应的权重、阈值、归一化参数、反归一化参数,记录好网络结构中你使用的激活函数,利用激活函数和矩阵运算复现网络。经验表明,归一化时需要归一化到【-1,1】范围内,能够完美复现网络。
ps_input %归一化参数
ps_output%返归一化参数
W1=net.IW{1,1};
W2=net.LW{2,1};
B1=net.b{1} ;
B2=net.b{2} ;
具体操作可以参考下文:
- Matlab训练好BP神经网络后,怎么根据权值和阈值来计算呢?
七、传统BP训练与自适应学习率+动量学习训练对比
以拟合函数f(x)=cos(x)为例(这里只考虑训练方法的对比,未对数据集进行划分):
- 分别以传统BP训练:traingd、自适应学习率+动量学习训练:traingdx、Levenberg-Marquadt:tranlm
传统BP训练:traingd (时间长、收敛慢)
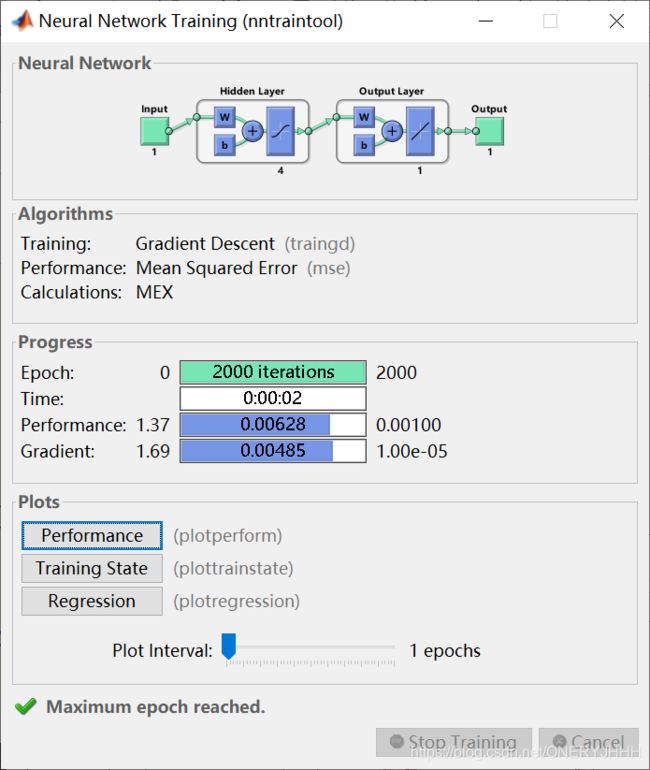
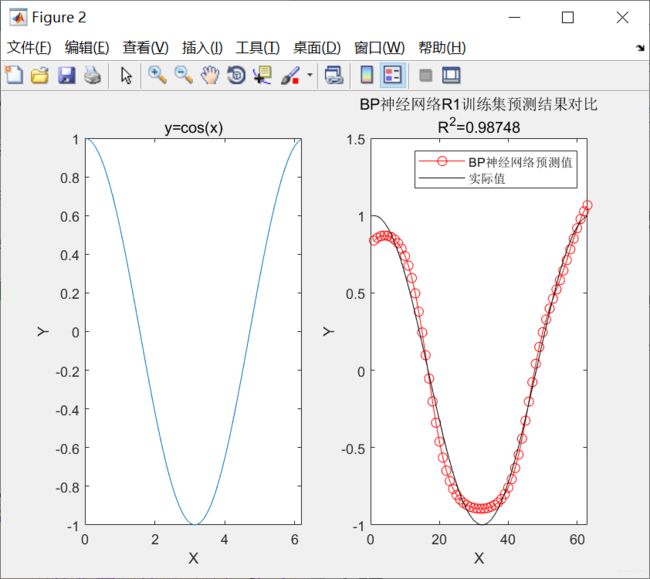
自适应学习率+动量学习训练:traingdx (时间较短、收敛较快)
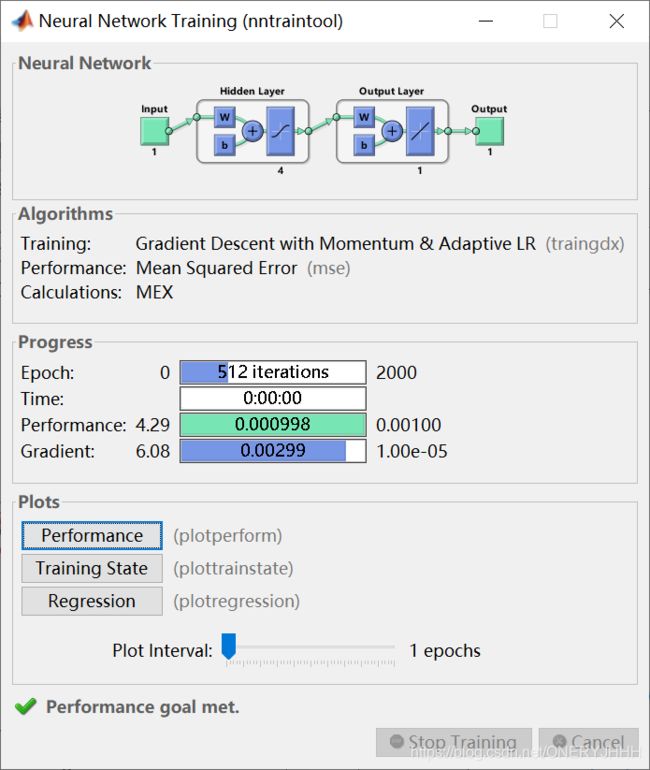
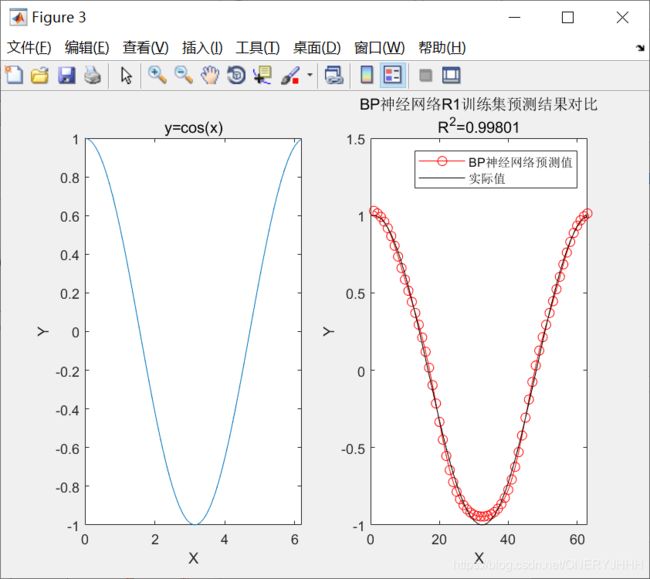
Levenberg-Marquadt:tranlm (时间段、收敛快)
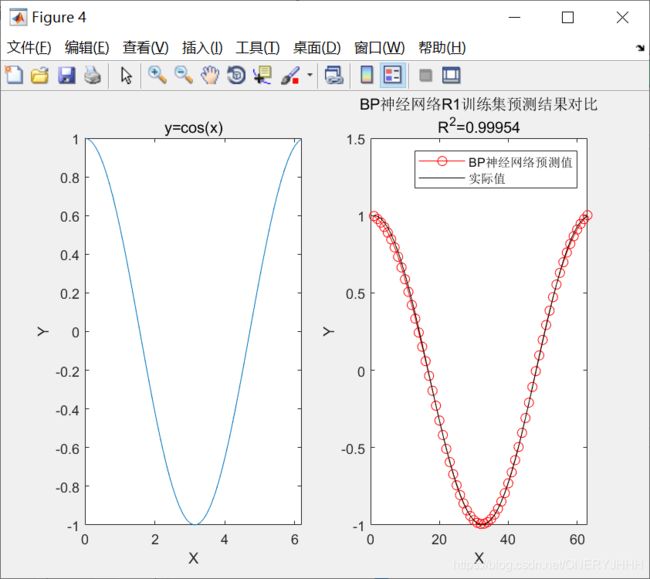
源码:
clc;
clear;
x=0:0.1:2*pi;
y=cos(x);
%% I.数据读取
p_train=x;
t_train=y;
%% II.数据归一化
[P_train, ps_input] = mapminmax(p_train,-1,1);
[T_train, ps_output] = mapminmax(t_train,-1,1);
p = P_train;
t = T_train;
%% III.BP神经网络建立
% 1.创建网络
net = newff(p,t,4,{'tansig','purelin'},'trainlm');
% net = newff(p,t,4,{'tansig','purelin'},'traingd');
% net = newff(p,t,4,{'tansig','purelin'},'traingdx');
% 2.设置训练参数
net.trainParam.epochs = 2000; %运行次数
net.trainParam.goal = 1e-3; %目标误差
net.trainParam.lr = 0.035; %学习率
net.trainParam.mc = 0.85; %动量因子
net.divideFcn = ''; %清除样本数据分为训练集、验证集和测试集命令
%%
% 3. 训练网络
net = train(net,p,t);
%%
% 4. 仿真测试
t_sim =sim(net,p);
%%
% 5. 数据反归一化
T_sim = mapminmax('reverse',t_sim,ps_output);
%% IV.拟合评价
r2_bp = 1 - (sum((T_sim'- t_train').^2) ./ sum(( t_train' - mean(t_train')).^2))
%% V.绘值训练对比图
figure;
subplot(1,2,1)
plot(x,y);
xlabel('X');
ylabel('Y');
title('y=cos(x)');
subplot(1,2,2)
plot(1:length(T_sim),T_sim,'r-o',1:length(T_sim),t_train,'k-');
legend('BP神经网络预测值','实际值');
xlabel('X');
ylabel('Y');
string = {'BP神经网络R1训练集预测结果对比';['R^2=' num2str(r2_bp)]};
title(string);
总结
本文主要目的是针对自己在学习和做项目过程中应用BP神经网络的经验做一些总结。内容主要包括基于MATLAB的BP神经网络设计步骤以及相关优化方面的介绍,还有过程中自己的杂七杂八的想法,如果大家有想法或者疑问欢迎私聊或者评论!!!
同时,如果在模型搭建、模型优化方面有相关需求 可以闲鱼搜索用户:Man小洁,欢迎交流。