海鸥优化算法(Seagull Optimization Algorithm,SOA)
目录
- 1 算法思想
- 2 算法步骤
- 3 求解函数最值(Python实现)
- 4 算法进阶
-
- 直接改进SOA
- 融合别的智能优化算法来改进SMA
- SMA及其改进的应用
原论文:
[1]Gaurav Dhiman, Vijay Kumar. Seagull optimization algorithm: Theory and its applications for large-scale industrial engineering problems. Knowledge-Based Systems. 2019(165), 169-196.
1 算法思想
借鉴生物行为:
海鸥的迁徙和攻击行为。海鸥根据季节更替进行迁徙,迁徙飞行时海鸥会避免相互碰撞;海鸥会攻击猎物,攻击时呈螺旋形的运动形态;在一个群体中,海鸥朝着最佳位置的方向前进。
2 算法步骤
- 初始化参数;
- 初始化种群位置;
- 计算适应度值并保留全局最优位置;
- 迁徙,全局搜索:
抽象海鸥的迁徙行为主要有三步,第一要满足避免碰撞条件(这样可以确保种群多样性);第二要计算最佳位置的方向;第三要根据该方向移动到新的位置。
第一,计算不与相邻海鸥碰撞的新位置 C s ( t ) C_s(t) Cs(t):
C s ( t ) = A × P s ( t ) A = f c − ( t × f c M a x i t e r a t i o n ) C_s(t)=A×P_s(t) \\ A = f_c-(t×\frac{f_c}{Max_{iteration}}) Cs(t)=A×Ps(t)A=fc−(t×Maxiterationfc)
其中, P s ( t ) P_s(t) Ps(t)为当前位置;t为当前迭代次数;A为海鸥在搜索空间中的运动行为; f c f_c fc为控制A变化频率的函数,从2线性递减到0; M a x i t e r a t i o n Max_{iteration} Maxiteration为最大迭代次数。
第二,计算最佳位置的方向 M s ( t ) M_s(t) Ms(t):
M s ( t ) = B × ( P b e s t ( t ) − P s ( t ) ) B = 2 × A 2 × r M_s(t)=B×(P_{best}(t)-P_s(t)) \\ B=2×A^2×r Ms(t)=B×(Pbest(t)−Ps(t))B=2×A2×r
其中, P b e s t ( t ) P_{best}(t) Pbest(t)为当前最佳位置; P s ( t ) P_s(t) Ps(t)为当前位置;B为平衡全局与局部搜索能力的随机数;r为[0,1]内的随机数。
第三,根据该方向移动到新位置 D s ( t ) D_s(t) Ds(t):
D s ( t ) = ∣ C s ( t ) + M s ( t ) ∣ D_s(t)=|C_s(t)+M_s(t)| Ds(t)=∣Cs(t)+Ms(t)∣ - 攻击猎物,局部搜索:
海鸥攻击猎物时在空中进行螺旋运动,抽象到三维空间中为:
{ x = r c o s ( θ ) y = r s i n ( θ ) z = r θ r = u × e θ v \left\{ \begin{aligned} & x=rcos(\theta) \\ & y=rsin(\theta) \\ & z=r\theta \\ & r=u×e^{\theta v} \end{aligned} \right. ⎩ ⎨ ⎧x=rcos(θ)y=rsin(θ)z=rθr=u×eθv
其中,r为螺旋半径,会越来越小; θ \theta θ为[0, 2π]内的随机角度值;u和v是两个决定螺旋形状的参数,轨迹模拟出来大概是这个样子:
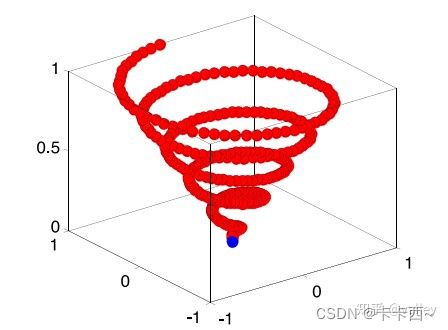
海鸥攻击猎物后的新位置 P s ( t ) P_s(t) Ps(t):
P s ( t ) = D s ( t ) × x × y × z + P b e s t ( t ) P_s(t)=D_s(t)×x×y×z+P_{best}(t) Ps(t)=Ds(t)×x×y×z+Pbest(t)
6. 判断是否满足终止条件,若不满足,返回步骤3。
3 求解函数最值(Python实现)
求解下列函数的最小值:
f ( x 1 , x 2 ) = x 1 2 + x 2 2 f(x_1,x_2)=x_1^2+x_2^2 f(x1,x2)=x12+x22
标准答案是0,函数长这个样子:
![]()
主函数:
import numpy as np
from matplotlib import pyplot as plt
import SOA
'''适应度函数'''
def fun(X):
Results = np.sum(X ** 2)
return Results
'''主函数 '''
#设置参数
pop = 30 #种群数量
MaxIter = 200 #最大迭代次数
dim = 2 #维度
lb = -10*np.ones(dim) #下边界
ub = 10*np.ones(dim)#上边界
#适应度函数选择
fobj = fun
GbestScore,GbestPositon,Curve = SOA.SOA(pop,dim,lb,ub,MaxIter,fobj) # 调用SOA函数
print('最优适应度值:',GbestScore)
print('最优解:',GbestPositon)
SOA.py:
import numpy as np
import copy
'''海鸥优化算法'''
'''
输入:
pop:种群数量
dim:每个个体的维度
lb:个体下边界,维度为[1,dim]
ub:个体上边界,维度为[1,dim]
MaxIter:最大迭代次数
fun:适应度函数接口
输出:
GbestScore:最优解对应的适应度值
GbestPositon:最优解
Curve:画迭代图用
'''
def SOA(pop, dim, lb, ub, MaxIter, fun):
# 1.初始化参数
Curve = np.zeros([MaxIter, 1]) # 画迭代图用
CS = np.zeros([pop, dim]) # 海鸥迁徙过程用到的三个变量,CS为满足避免碰撞条件的位置
MS = np.zeros([pop, dim]) # MS为最佳位置的方向
DS = np.zeros([pop, dim]) # DS为最终迁徙完得到的新位置
fc = 2 # ???论文中的fc从2线性递减到0,可以控制变量A的变化频率,第4.1步用
u = 1 # 螺旋形状的相关参数,第5步用
v = 1 # 螺旋形状的相关参数,第5步用
# 2.根据种群数量与边界来初始化种群位置
X = initialization(pop, ub, lb, dim) # 初始化种群
# 3.计算适应度值并保留全局最优值
fitness = CaculateFitness(X, fun) # 计算适应度值
fitness, sortIndex = SortFitness(fitness) # 对适应度值排序,得到排序后的适应度值和对应的索引
X = SortPosition(X, sortIndex) # 根据排序后的索引对种群排序
GbestScore = copy.copy(fitness[0]) # 此时fitness的第一个值为最好的适应度值
GbestPositon = np.zeros([1, dim])
GbestPositon[0, :] = copy.copy(X[0, :]) # 此时X的第一个值为最好的个体
X_new = copy.copy(X)
for i in range(MaxIter):
# print("第"+str(i)+"次迭代")
Pbest = X[0, :]
for j in range(pop):
# 4.1计算Cs,得到避免碰撞的位置,保持种群多样性,全局搜索
A = fc - (i * (fc / MaxIter))
CS[j, :] = X[j, :] * A
# 4.2计算Ms,得到最佳位置的方向
rd = np.random.random()
B = 2 * (A ** 2) * rd
MS[j, :] = B * (Pbest - X[j, :])
# 4.3计算Ds,到达新位置
DS[j, :] = np.abs(CS[j, :] + MS[j, :])
# 5.海鸥进行螺旋运动攻击猎物,局部搜索
# 螺旋形状
theta = np.random.random()
r = u * np.exp(theta * v) # theta为[0,1]
x = r * np.cos(theta * 2 * np.pi) # theta为[0,2π]
y = r * np.sin(theta * 2 * np.pi) # theta为[0,2π]
z = r * theta # theta为[0,1]
# 攻击猎物后的位置
X_new[j, :] = x * y * z * DS[j, :] + Pbest
X = BorderCheck(X_new, ub, lb, pop, dim) # 边界检查
fitness = CaculateFitness(X, fun) # 计算适应度值
fitness, sortIndex = SortFitness(fitness) # 对适应度值排序,拿到索引
X = SortPosition(X, sortIndex) # 根据索引对种群排序
if (fitness[0] <= GbestScore): # 更新全局最优
GbestScore = copy.copy(fitness[0])
GbestPositon[0, :] = copy.copy(X[0, :])
Curve[i] = GbestScore
return GbestScore, GbestPositon, Curve
运行结果:
最优适应度值: [6.28823104e-226]
最优解: [[-1.77578646e-113 1.77054045e-113]]
可以看到答案非常接近最优适应度值0。
4 算法进阶
- 在标准测试函数、CEC2014测试函数中表现一般;
- 标准工程优化设计问题上SOA优势很大;
- 螺旋行为与鲸鱼优化算法有些相似;
- 原文中的公式与作者上传的源码里的公式有差异;
- 在迭代前期收敛速度很慢,容易陷入局部最优值;
- 虽然当前个体确实没有和其他个体存在位置冲突,但是在螺旋飞行的过程中难免会存在个体碰撞,全局搜索能力不如想象的好;
- 优化Quadric函数(F3)存在问题,与全局最优相差上万;
- 优化Rosenbrock函数(F5)效果不好,与全局最优相差4;
- 优化Rastrigin函数Griewank(F9,11,16,18)效果好,能找到全局最优;
直接改进SOA
| 文献 | 改进策略 |
|---|---|
| 王培崇,尹欣洁,李丽荣.一种具有学习机制的海鸥优化算法[J].郑州大学学报(工学版),2022,43(06):8-14. | 反向学习 |
| 龙文,徐明,羊洋.用于函数优化和特征选择的翻筋斗觅食海鸥优化算法[J/OL].计算机应用研究:1-7[2022-10-19]. | 翻筋斗觅食策略 |
| 严爱军,胡开成.提高海鸥优化算法寻优能力的改进策略及其应用[J/OL].信息与控制:1-11[2022-10-19]. | 并行搜索+反向学习+马尔可夫过程 |
| 王娟,秦江涛.混沌映射与t-分布变异策略改进的海鸥优化算法[J].计算机应用研究,2022,39(01):170-176+182. | tent混沌映射+t分布变异 |
| 王宁,何庆.融合黄金正弦与sigmoid连续化的海鸥优化算法[J].计算机应用研究,2022,39(01):157-162+169. | sigmoid连续化 |
| 秦维娜,张达敏,尹德鑫,蔡朋宸.一种基于非线性惯性权重的海鸥优化算法[J].小型微型计算机系统,2022,43(01):10-14. | 非线性惯性权重+莱维飞行机制 |
| 毛清华,王迎港.融合改进Logistics混沌和正弦余弦算子的自适应t分布海鸥算法[J/OL].小型微型计算机系统:1-9[2022-10-19]. | Logistics混沌映射+t分布变异 |
融合别的智能优化算法来改进SMA
| 文献 | 融合的智能优化算法 |
|---|---|
| 王宁,何庆.融合黄金正弦与sigmoid连续化的海鸥优化算法[J].计算机应用研究,2022,39(01):157-162+169. | 黄金正弦 |
| 丁飞,江铭炎.基于改进狮群算法和BP神经网络模型的房价预测[J].山东大学学报(工学版),2021,51(04):8-16. | 狮群算法LSO |
| 毛清华,王迎港.融合改进Logistics混沌和正弦余弦算子的自适应t分布海鸥算法[J/OL].小型微型计算机系统:1-9[2022-10-19]. | 正余弦 |
SMA及其改进的应用
| 文献 | 应用 |
|---|---|
| 龙文,徐明,羊洋.用于函数优化和特征选择的翻筋斗觅食海鸥优化算法[J/OL].计算机应用研究:1-7[2022-10-19]. | 特征选择 |
| 丁飞,江铭炎.基于改进狮群算法和BP神经网络模型的房价预测[J].山东大学学报(工学版),2021,51(04):8-16. | BP神经网络+房价预测 |
| Improved seagull optimization algorithm of partition and XGBoost of prediction for fuzzy time series forecasting of COVID-19 daily confirmed | xgboost+时间序列预测 |
| 王瑞. 基于改进海鸥优化算法的智能工厂柔性作业车间调度问题研究[D].燕山大学,2021. | 作业车间调度问题 |
| 程亚南,王晓峰,刘凇佐,刘子琳,张九龙.一种求解TSP问题的海鸥算法[J].现代电子技术,2022,45(07):112-116. | 旅行商问题 |
参考书籍:范旭,《Python智能优化算法——从原理到代码实现与应用》第一版,电子工业出版社。