理解 CNN

理解 CNN

注意：下面提到的图像指位图

CNN

卷积神经网络-CNN 最擅长的就是图片的处理。它受到人类视觉神经系统的启发。

CNN的两大特点：

• 能够有效的将大数据量的图片降维成小数据量
• 能够有效的保留图片特征，符合图片处理的原则

人类的视觉原理

详见：浅谈人类视觉系统与卷积神经网络（CNN）的联系和区别

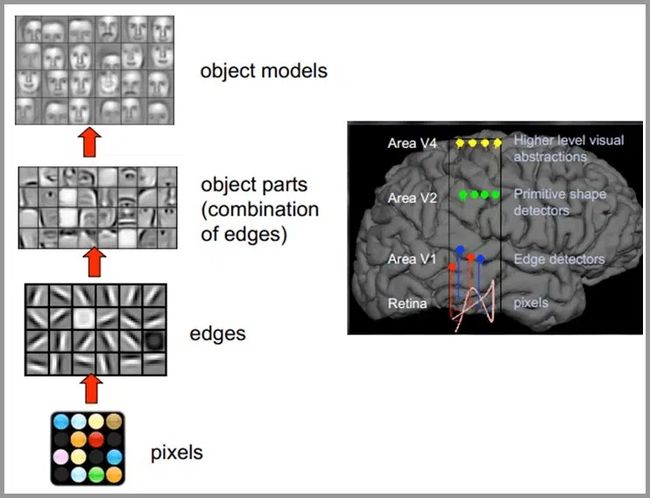
深度学习的许多研究成果，离不开对大脑认知原理的研究，尤其是视觉原理的研究。

1981 年的诺贝尔医学奖，颁发给了 David Hubel（出生于加拿大的美国神经生物学家） 和TorstenWiesel，以及 Roger Sperry。前两位的主要贡献，是“发现了视觉系统的信息处理”，可视皮层是分级的。

人类的视觉原理如下：从原始信号摄入开始（瞳孔摄入像素 Pixels），接着做初步处理（大脑皮层某些细胞发现边缘和方向），然后抽象（大脑判定，眼前的物体的形状，是圆形的），然后进一步抽象（大脑进一步判定该物体是只气球）。下面是人脑进行人脸识别的一个示例：

其实对于我们看不同的物体也是类似的，在最底层基本上是类似的。先是看各种边缘，越往上，就越能提取出此类物体的一些特征（鼻子、眼睛、嘴巴），到最上层，不同的高级特征最终组合成相应的图像，从而能够让人类准确区分不同的物体。这种逐层提取信息的方式就是许多深度学习算法（包括CNN）的灵感来源。

后面我们就来通过对几个层的讲解来对CNN有进一步的了解。

几个关键层

典型的CNN一般由3个部分构成：

1. 卷积层
2. 池化层
3. 全连接层

名称	作用简述
卷积层	提取图像特征
池化层	降维、防止过拟合
全连接层	输出结果

卷积层(fliter、kernel)

在这部分我们来看一下卷积的过程。假设我们要提取出下面这个$5\times 5$ 的矩阵的特征（其实位图图像存储底层就是通过这种矩阵的方式存储的，不过位图一般有r、g、b三层的矩阵信息）。

同时我们定义一个$3\times 3$的矩阵，在CNN中其实被称作 filter 或 kernel 或 feature detector。

ok有了前面一个输入矩阵和 kernel 矩阵的定义，我们可以观察下图看看， kernel是如何对输入矩阵的特征进行提取的。其实很简单，就是每次将 kernel中的元素与输入矩阵中的每个元素对应相乘然后累加，得到 Convolved Feature 中的一个元素。

针对上述例子的附加解释，顺便讲解一下torch.nn.Conv1d 的参数 ：

• in_channels(输入通道数): 前面提到了我们的输入矩阵是只有一个，其实对应的就是in_channels = 1,如果说是那种位图信息输入包含r、g、b三层矩阵信息的话 in_channels = 3。

• out_channels(输出通道数): 卷积产生的通道。有多少个 out_channels,就需要多少一个1维卷积。例如上图中只输出了一个 Convoled Feature所以 out_channels = 1。

• stride(步长): 卷积步长其实指的就是 kernel 在与输入矩阵进行计算的时候，每次移动的步数，这里stride = 1。这可以理解为一个动态的过程，可以观察上图， kernel每次移动都是向一个方向平移一格。

• kernel_size(核的大小): kernel_size指的就是 kernel的大小。上面对应的是一个二维的卷积，kernel_size = (3 * 3)。

• padding: 输入的每一条边补充0的层数。换一个说法就是，我们比较案例中的Image和Convolved Feature的维度，因为卷积的时候是没加padding的所以让卷积后维度下降。如果我们设置padding = 1, 作用就是在进行卷积的时候，会先对Image的最外一圈用0去扩充。可以让最后得到的卷积的结果与原始Image一致。

  

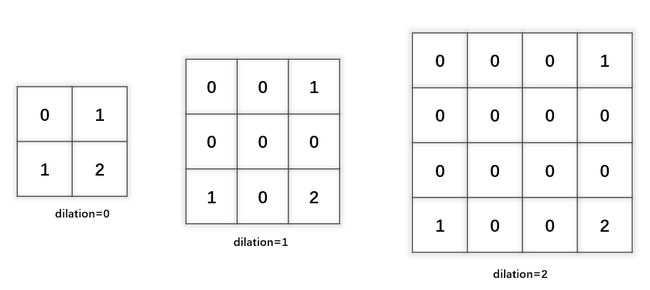
• dilation(卷积核膨胀): 卷积核的膨胀，设置的是卷积核元素的间隔，如下图所示：

  

• groups: 从输入通道到输出通道的阻塞连接数。当groups=1的时候，假设此时 输入的通道数为n，输出的通道数为m，那么理解为把输入的通道分成1组(不分组)，每一个输出通道需要在所有的输入通道上做卷积，也就是一种参数共享的局部全连接。如果把groups改成2，可以理解为把 输入的通道分成两组，此时每一个输出通道只需要在其中一组上做卷积。如果groups=in_channels，也就是把 输入的通道分成in_channels组(每一组也就一个通道)，此时每一个输出通道只需要在其中一个输入通道上做卷积。

• bias: 如果bias = True，则添加偏置，偏置就是用来在卷积得到的结果后加上一个项，以调整整个数据的区间。因为卷积的结果后面是要输入到激活层的嘛，我们可以通过下图看bias对这个数据的影响。其实本质的意思就是有了偏置项让数据整体分布上有了平移的效果，从而根激活函数更好地配合起来。

  

用例

import torch
import torch.nn as nn

d = torch.Tensor(3, 5)
conv = nn.Conv1d(
  in_channels=3,
  out_channels=2,
  kernel_size=2,
  padding=1,
  stride=2,
  bias=True,
)
print(d)
print(conv.weight)
print(conv(d))

"""
## Output
## 因为torch.nn中设置的卷积核(kernel)内的数据是随机的，运行的时候输出可能会不一样但数据的维度应当是一样的
tensor([[4.9592e-39, 4.2246e-39, 1.0286e-38, 1.0653e-38, 1.0194e-38],
        [8.4490e-39, 1.0469e-38, 9.3674e-39, 9.9184e-39, 8.7245e-39],
        [9.2755e-39, 8.9082e-39, 9.9184e-39, 8.4490e-39, 9.6429e-39]])
Parameter containing:
tensor([[[ 0.3349,  0.2759],
         [-0.0143, -0.3235],
         [-0.2177, -0.0688]],

        [[ 0.2330,  0.3502],
         [-0.3834, -0.0521],
         [-0.1585,  0.3144]]], requires_grad=True)
tensor([[-0.0977, -0.0977, -0.0977],
        [-0.2637, -0.2637, -0.2637]], grad_fn=)
"""

卷积后得到 OutPutShape

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Qcf7pu33-1669972715833)(https://raw.githubusercontent.com/yuyuyu258963/pic-go-picStore/main/%E5%8D%B7%E7%A7%AFOutputShape%E8%AE%A1%E7%AE%97.png)]

我们可以通过下图的例子进一步理解卷积的过程。

池化层 (pooling)

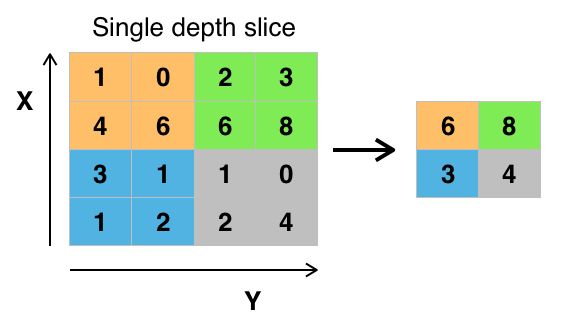
池化层（Pooling）是卷积神经网络中另一个重要的概念，它实际上是一种形式的降采样。有多种不同形式的非线性池化函数，而其中“最大池化（Max pooling）”是最为常见的。它是将输入的图像划分为若干个矩形区域，对每个子区域输出最大值。直觉上，这种机制能够有效地原因在于，在发现一个特征之后，它的精确位置远不及它和其它特征的相对位置的关系重要。池化层会不断地减小数据的空间大小，因此参数的数量和计算量也会下降，这在一定程度上也控制了过拟合。通常来说，CNN的卷积层之间都会周期性地插入池化层。

池化层通常会分别作用域每个输入的特征并减小其大小。当前最常用形式的池化层是每隔2个元素从图像划分出$2\times 2$的区块，然后对每个区块中的4个数取最大值。这将会减少75%的数据量。

池化的作用

池化操作后的结果相比其输入缩小了。池化层的引入是仿照人的视觉系统对视觉输入对象进行降维和抽象。在卷积神经网络过去的工作中，研究者普遍认为池化层有如下三个功效：

1. 特征不变性：池化操作是模型更加关注是否存在某些特征而不是特征具体的位置
2. 特征降维：池化相当于在空间范围内做了维度约减，从而使模型可以抽取更加广阔的特征。同时减少了下一层的输入大小，进而减少计算量和参数个数
3. 在一定程度上防止过拟合：更方便优化

用例

import numpy as np
import torch

d = np.array([[1.0,0.0,1.0,2.0,3.0,4.0]])
input = torch.from_numpy(d)
print(input)
"""ouput
tensor([[1., 0., 1., 2., 3., 4.]], dtype=torch.float64)
"""
import torch.nn.functional as F
ouput = F.max_pool1d(input, kernel_size = 2, stride = 1)
print(ouput)
ouput = F.avg_pool1d(input, kernel_size = 2, stride = 1)
print(ouput)
"""ouput
tensor([[1., 1., 2., 3., 4.]], dtype=torch.float64)
tensor([[0.5000, 0.5000, 1.5000, 2.5000, 3.5000]], dtype=torch.float64)
"""

上述的用例中展示了，最大池化（MaxPooling）和平均池化（AvgPooling）的用例。因为池化也涉及到这个子区域的选择嘛，所以里面的一些参数就和前面的torch.nn.Conv1d中的参数很类似。

激活层(activate)

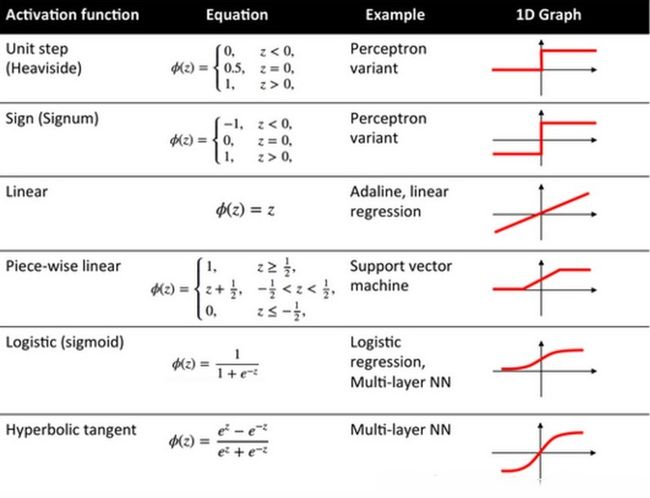
激活层里面其实就是激活函数，就是在人工神经网络的神经元上运行的函数，负责将神经元的输入映射到输出端。

激活函数对于人工神经网络模型去学习、理解非常复杂和非线性的函数来说具有非常重要的作用。它们将给线性特性引入到我们的网络中。引入激活函数是为了增加神经网络模型的非线性。没有激活函数的每层都相当于矩阵相乘。就算你叠加了若干层之后，无非还是个矩阵相乘罢了。

下面是一张关于常见激活函数的表：

全连接层(Linear)

全连接层在整个CNN网络中起到“分类器”的作用。如果说前面的卷积层、池化层和激活函数等操作是将原始数据映射到隐层特征空间，全连接层起到的将学到的特征表示映射到样本的标记空间的作用。

全连接层实现原理

---

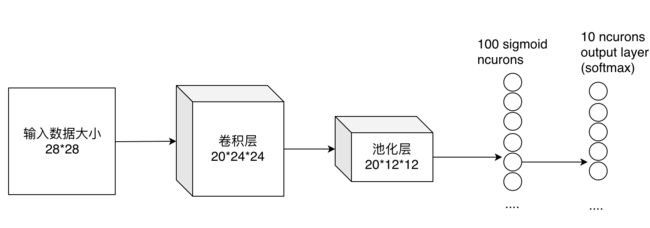
在卷积神经网络的最后，往往会出现一两层全连接层，全连接一般会把卷积输出的二维特征图转化为一维的向量。如上图中最后两列表示的就是两个全连接层，在最后一层卷积结束后，进行了最后一次池化，输出了20个$12\times 12$的图像，然后通过了一个全连接层变成了$1\times 100$的向量。这么一看前面的工作我么做的就是一个降维的操作，然后我们将得到的向量输入全连接层进行输出。

用例

input = torch.Tensor(1, 10)
linear = nn.Linear(10, 2)
print(input)
print(linear(input))
"""output
tensor([[5.1429e-39, 4.5000e-39, 4.9592e-39, 4.2246e-39, 1.0286e-38, 1.0653e-38,
         1.0194e-38, 8.4490e-39, 1.0469e-38, 9.3674e-39]])
tensor([[-0.1961,  0.2197]], grad_fn=)
"""

比如用例中我们可能在前面得到了一个一百维的向量，然后这个任务的是一个二分类的任务。我们就可以设置通过全连接层输出的向量维度为(1,2)。其中的2与二分类任务对应。上面输出的tensor([[-0.1961, 0.2197]]，那么一般来说我们认为这个得到的分类结果是第2类。

pytorch实现TextCNN

class TextCNN(nn.Module):
  def __init__(self, vocab_size, embedding_dim, kernel_sizes, num_channels, dropout, vectors=None):
    super(TextCNN, self).__init__()
    self.word_embeddings = nn.Embedding(vocab_size, embedding_dim)  # embedding之后的shape: torch.Size([200, 8, 300])
    if vectors is not None:
      self.word_embeddings = self.word_embeddings.from_pretrained(vectors, freeze=False)
    # dropout 代表每个神经元不被激活的概率
    self.dropout = nn.Dropout(dropout)
    self.decoder = nn.Linear(sum(num_channels), 2)
    # 时序最大池化层没有权重，所以可以共用一个实例
    self.pool = F.GlobalMaxPool1d()
    self.convs = nn.ModuleList([
      nn.Sequential(
        nn.Conv1d(
                  in_channels = embedding_dim, 
                  out_channels = c, 
                  kernel_size = k
                  ),
        nn.ReLU(),
        nn.MaxPool1d(2, padding=1),
      )
      for c, k in zip(num_channels, kernel_sizes)
    ])  # 创建多个一维卷积层

  def forward(self, sentence):
    embeds = self.word_embeddings(sentence)
    embeds = embeds.permute(0, 2, 1)
    # 对于每个一维卷积层，在时序最大池化后会得到一个形状为(批量大小, 通道大小, 1)的
    # Tensor。使用flatten函数去掉最后一维，然后在通道维上连结
    encoding = torch.cat([self.pool(conv(embeds)).squeeze(-1) for conv in self.convs], dim=1)
    # 应用丢弃法后使用全连接层得到输出
    outputs = self.decoder(self.dropout(encoding))
    return outputs

卷积传播图解

先来看得到卷积的过程

(单个元素的梯度计算)不考虑前后的层，比如我们已经得到了Delta Output的梯度矩阵，可以观察下图如何得到在原矩阵中$x_{2,2}$的梯度值。

(推广到全部元素) 这里就是对Delta d做了一个padding之后然后反向做了卷积。

不同视角看CNN

这部分图来自：https://cloud.tencent.com/developer/article/1594092

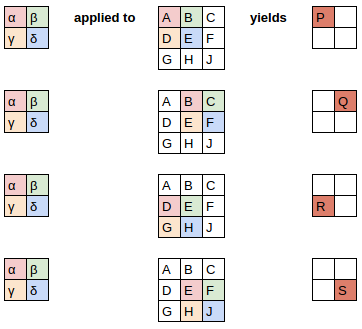
比如有原始数据矩阵：

filter

得到的Convoled Feature：

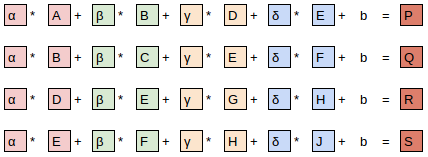
卷积计算的视角

等式计算角度

网络角度

矩阵乘法角度

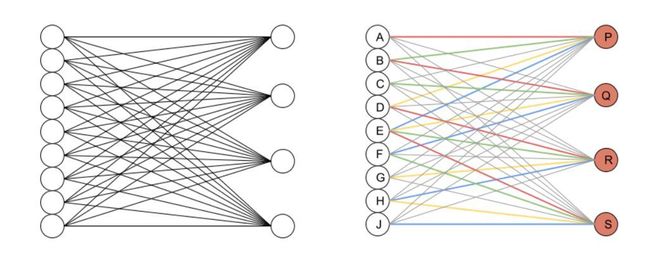
Dense神经网络角度

在这个角度下我们可以更好地理解传统神经网络和CNN之间的联系，其中左图是传统神经网络，右图数Dense神经网络视角下的CNN。灰度连接对应于不可训练的0.

参考

• 多视角理解CNN
• 神经网络中偏置的作用
• 卷积核膨胀解析
• PyTorch 中文文档
• https://easyai.tech/ai-definition/cnn/