【深度学习】图像分类之KNN算法
文章目录
- 前言
- 一、CIFAR-10 数据集简介
- 二、Nearest Neighbor Classifier(最近邻分类器)
-
- L1距离(曼哈顿距离)
- L2距离(欧氏距离)
- 三、k - Nearest Neighbor (KNN算法)
-
- K值的设置
-
- 训练集、验证集、测试集
- 交叉验证
前言
图像分类任务是,分类系统预先知道一些确定了分类或标签的集合,这些标签有可能是猫咪或者狗狗。系统接收一些输入图像,比如说猫咪,然后根据算法给输入的图片分配一些固定的标签。
这对人的视觉系统来说是微不足道,但对于机器来说是很有挑战的。
图像分类模型采用单个图像并将概率分配给 4 个标签{cat, dog, hat, mug}。如图所示,请记住,对于计算机而言,图像表示为一个大型 3 维数字数组。在本例中,猫的图像宽 248 像素,高 400 像素,具有红色、绿色、蓝色(或简称 RGB)三个颜色通道。因此,图像由 248 x 400 x 3 个数字组成,或总共 297,600 个数字。每个数字都是一个整数,范围从 0(黑色)到 255(白色)。我们的任务是将这 25 万个数字变成一个标签,例如“猫”。
 图像分类中的任务是预测给定图像的单个标签(或此处显示的标签分布以指示我们的置信度)。图像是从 0 到 255 的整数的 3 维数组,大小为 Width x Height x 3。3 代表红、绿、蓝三个颜色通道。
图像分类中的任务是预测给定图像的单个标签(或此处显示的标签分布以指示我们的置信度)。图像是从 0 到 255 的整数的 3 维数组,大小为 Width x Height x 3。3 代表红、绿、蓝三个颜色通道。
一、CIFAR-10 数据集简介
一种流行的玩具图像分类数据集,该数据集由 60,000 张高和宽 32 像素的微小图像组成。每个图像都标有 10 个类别之一(例如“飞机、汽车、鸟等”)。这 60,000 张图像被划分为 50,000 张图像的 训练集 和 10,000 张图像的 测试集。
 左:来自CIFAR-10 数据集的示例图像。右图:第一列显示了一些测试图像,在每个测试图像旁边,我们根据像素差异显示了训练集中的前 10 个最近邻。
左:来自CIFAR-10 数据集的示例图像。右图:第一列显示了一些测试图像,在每个测试图像旁边,我们根据像素差异显示了训练集中的前 10 个最近邻。
二、Nearest Neighbor Classifier(最近邻分类器)

其实我们可以看到,10 个示例测试图像的示例结果并没有很准确。这是因为最邻近算法并不是很健壮,下面是算法的具体内容:
假设我们有 50,000 张图像的 CIFAR-10 训练集(每个标签 5,000 张图像),我们希望标记剩余的 10,000 张图像。最近邻分类器将获取一张测试图像,将其与每一张训练图像进行比较,并预测最近的训练图像的标签。
L1距离(曼哈顿距离)
比较两张图像的细节,其实就是两个 32 x 32 x 3 的块。最简单的方法之一是:逐比较图像每一个像素点的差值,并将所有差值的绝对值相加。换句话说,给定两个图像并将它们表示为向量I1,I2,使用L1 距离来对他们进行比较:
 下面是4*4的图像一个具体实例:
下面是4*4的图像一个具体实例:
 如果两个图像相同,则结果将为零。但如果图像非常不同,结果会很大。
如果两个图像相同,则结果将为零。但如果图像非常不同,结果会很大。
下面是分类器实现代码:
#首先,让我们将 CIFAR-10 数据作为 4 个数组加载到内存中:训练数据/标签和测试数据/标签。
#Xtr(大小为 50,000 x 32 x 32 x 3)保存训练集中的所有图像,对应的一维数组Ytr(长度为 50,000)保存训练标签(从 0 到 9)
Xtr, Ytr, Xte, Yte = load_CIFAR10('data/cifar10/') # a magic function we provide
# flatten out all images to be one-dimensional
Xtr_rows = Xtr.reshape(Xtr.shape[0], 32 * 32 * 3) # Xtr_rows becomes 50000 x 3072
Xte_rows = Xte.reshape(Xte.shape[0], 32 * 32 * 3) # Xte_rows becomes 10000 x 3072
现在我们已经将所有图像拉伸成行,下面是我们如何训练和评估分类器:
nn = NearestNeighbor() # create a Nearest Neighbor classifier class
#我们构建的所有分类器都满足这一通用 API:它们具有一个train(X,y)函数,可以获取数据和标签以供学习。
nn.train(Xtr_rows, Ytr) # train the classifier on the training images and labels
#predict(X)函数,它接受新数据并预测标签
Yte_predict = nn.predict(Xte_rows) # predict labels on the test images
# and now print the classification accuracy, which is the average number
# of examples that are correctly predicted (i.e. label matches)
print 'accuracy: %f' % ( np.mean(Yte_predict == Yte) )
下面一个简单的最近邻分类器的实现:
import numpy as np
class NearestNeighbor(object):
def __init__(self):
pass
def train(self, X, y):
""" X is N x D where each row is an example. Y is 1-dimension of size N """
# the nearest neighbor classifier simply remembers all the training data
self.Xtr = X
self.ytr = y
def predict(self, X):
""" X is N x D where each row is an example we wish to predict label for """
num_test = X.shape[0]
# lets make sure that the output type matches the input type
Ypred = np.zeros(num_test, dtype = self.ytr.dtype)
# loop over all test rows
for i in range(num_test):
# find the nearest training image to the i'th test image
# using the L1 distance (sum of absolute value differences)
distances = np.sum(np.abs(self.Xtr - X[i,:]), axis = 1)
min_index = np.argmin(distances) # get the index with smallest distance
Ypred[i] = self.ytr[min_index] # predict the label of the nearest example
return Ypred
L2距离(欧氏距离)
另一个常见的计算向量之间距离的方法是使用L2距离:

也就是说,我们像L1一样计算像素差,然后将它们全部平方再相加起来,最后取平方根。在 numpy 中,使用上面的代码,我们只需要替换一行代码。计算距离的线:
distances = np.sqrt(np.sum(np.square(self.Xtr - X[i,:]), axis = 1))
三、k - Nearest Neighbor (KNN算法)
在上面算法中,当k = 1时,就是最近邻分类算法了。
简单介绍一下KNN:给你一张测试图片,用这个测试图片对训练集中的所有图片,做一个欧氏距离或其他的距离,就是做一个相似的衡量,衡量完后,做一个排序,相似度最近到最远,选出前k张,再对这k张进行一个投票,哪个标签数量最多,我们就指定他为哪个
KNN:在训练集中不是找到最接近的单个图像,而是会找到前k个最接近的图像,并让它们对测试图像的标签进行比较。直观地说,较高的k值具有平滑效果,使分类器更能抵抗异常值:
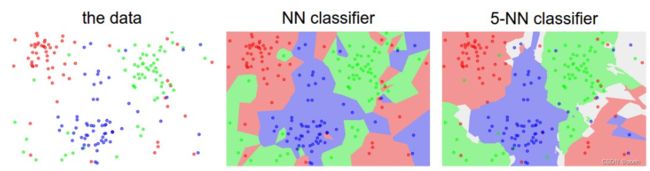 白色区域显示分类不明确的点(即班级投票与至少两个班级并列)。
白色区域显示分类不明确的点(即班级投票与至少两个班级并列)。
在 NN 分类器的情况下,异常数据点(例如蓝点云中间的绿点)会产生可能不正确的预测的小岛。
而 5-NN 分类器会平滑这些不规则性,可能会导致更好的泛化关于测试数据(未显示)。还要注意,5-NN 图像中的灰色区域是由最近邻居之间的投票关系造成的(例如,2 个邻居是红色的,接下来的两个邻居是蓝色的,最后一个邻居是绿色的)。
K值的设置
我们可以使用许多不同的距离函数:L1 范数、L2 范数,还有许多我们甚至没有考虑过的其他选择(例如点积)。这些选择被称为超参数,它们经常出现在许多从数据中学习的机器学习算法的设计中。
在调参时,一定要注意,不能使用测试集来调整超参数。理想情况下,直到最后一次才应该触及测试集(这就好像,你要考试了,答案不可以提前看,看了答案你就记住了题会怎么出,应该是考完才可以看)。
如果用测试集作为训练集,很容易出现过拟合问题。
训练集、验证集、测试集
有一种调整超参数的正确方法,它根本不会触及测试集。这个想法是将我们的训练集分成两部分:一个稍微小一点的训练集,以及一个验证集。以 CIFAR-10 为例,我们可以使用 49,000 个训练图像进行训练,并留出 1,000 个用于验证。这个验证集本质上被用作一个假测试集来调整超参数。
以下是 CIFAR-10 的情况:
# assume we have Xtr_rows, Ytr, Xte_rows, Yte as before
# recall Xtr_rows is 50,000 x 3072 matrix
Xval_rows = Xtr_rows[:1000, :] # take first 1000 for validation
Yval = Ytr[:1000]
Xtr_rows = Xtr_rows[1000:, :] # keep last 49,000 for train
Ytr = Ytr[1000:]
# find hyperparameters that work best on the validation set
validation_accuracies = []
for k in [1, 3, 5, 10, 20, 50, 100]:
# use a particular value of k and evaluation on validation data
nn = NearestNeighbor()
nn.train(Xtr_rows, Ytr)
# here we assume a modified NearestNeighbor class that can take a k as input
Yval_predict = nn.predict(Xval_rows, k = k)
acc = np.mean(Yval_predict == Yval)
print 'accuracy: %f' % (acc,)
# keep track of what works on the validation set
validation_accuracies.append((k, acc))
在这个过程结束时,我们可以绘制一个图表,显示哪些k值最有效。然后我们将坚持这个值并在实际测试集上评估一次。
将训练集拆分为训练集和验证集。使用验证集调整所有超参数。最后在测试集上运行一次并报告性能。
交叉验证
与其任意选择前 1000 个数据点作为验证集和其余训练集,可以对某个k的某个值的好坏获得更好、噪音更小的估计。通过迭代不同的验证集并平均这些验证集的性能来工作。例如,在 5 折交叉验证中,将训练数据分成 5 等份,其中 4 个用于训练,1 个用于验证。然后迭代哪一份用来验证,评估性能,最后对不同折叠的性能进行平均。
