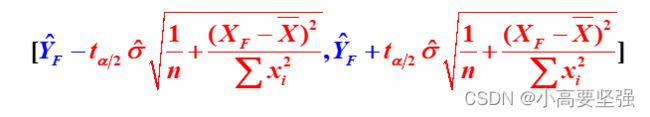简单线性回归模型
简单线性回归模型
研究经济变量之间相互数量关系最基本的方法之一是回归分析。在回归分析中,只有一个解释变量的线性回归模型是最简单的,称为简单线性回归模型或一元线性回归模型。本文主要从最简单的一元线性回归模型入手,讨论在基本假定满足的条件下,对经济变量关系进行计量的基本理论和方法。
第一节 回归分析与回归函数
一、相关分析与回归分析
(一)经济变量间的相互关系
在很多社会与经济现象中,除自身的变动外,它们相互之间很可能有一定的依存关系。各种经济变量相互之间的依存关系有两种不同的类型:一种是确定性的函数关系,另一种是不确定性的统计关系,也成为相关关系。
当一个或若干个变量X取一定数值时,某一个变量Y有确定的值与之对应,我们称变量间的这种关系为确定性的函数关系。一般情况下,确定性的函数关系可表示为Y=f(x)。
当一个或若干个变量X去一定数值时,与之相对应的另一个变量Y的值虽然不确定,但却按某种规律在一定范围内变化,我们称变量之间的这种关系为不确定性的统计关系或相关关系,一般可表示为Y=f(X,u),其中u为随机变量。例如居民可支配收入X,可能对应不同的消费Y,呈现出为不确定性的相关关系。
变量之间的相关关系可用坐标图(又称散点图)描述,变量之间的相关关系可以分为以下若干类型。
(1)从相关关系涉及的变量数量看。只有两个变量的相关关系称为简单相关关系。三个或三个以上变量的相关关系,称为多重相关或复相关。
(2)从变量相关关系的表现形式看。当变量之间相关关系的散点图的点接近一条直线时,称为线性相关;当变量之间相关关系散点图中的点接近于一条曲线时,称为非线性相关。
(3)从变量相关关系变化的方向看。两个变量趋于在同一方向变化时,即同增或同减,称为变量之间存在正相关。当两个变量趋于在相反方向变化时,即当一个变量增加时,另一个变量却减少,称为变量之间存在负相关。
(4)从变量相关的程度看。当一个变量的变化由另一个变量的变化确定时,称为变量之间完全相关。在这种情况下,相关关系实际成了函数关系,所以可以把函数关系视为相关关系的特例。
当两个变量的变化相互完全没有关系,即彼此互不影响,称为二者不相关。两个现象的关系如果介于完全相关和不相关之间时,称为不完全相关,我们研究的相关关系通常是指的这种不完全的相关关系。
(二)简单线性相关关系的度量
- 简单线性相关系数
在各种类型的相关分析中,只有两个变量的线性相关关系的分析是最简单的。两个变量之间线性相关程度可以用简单线性相关系数去度量,这种相关系数是最常用的,简称为相关系数。对于我们所研究的总体,两个相互联系的变量的相关系数称为总体相关系数,通常用p表示,总体相关系数p可用下式计算:

式中,Var(X)是变量X的方差;Var(Y)是变量Y的方差;Cov(X,Y)是变量X和Y的协方差。
总体相关系数p反映了总体两个变量X和Y的线性相关程度,对于特定总体来说,X和Y的数值是既定的,所以总体相关系数p是客观存在的特定数值。但对于总体较大时,X和Y的数值不可能去直接观测时,总体相关系数就不能直接计算。通常可能做到的是从总体中随机抽取一定数量的样本,通过X和Y的样本观测值去计算样本相关系数,变量X和Y的样本相关系数通常用rxy来表示,或简记为r,可用下式去估计:

式中,Xi和Yi分别是变量X和变量Y的样本观测值;n为样本的个数,也称样本容量。
样本相关系数r是根据总体中抽取的随机样本的观测值Xi和Yi计算出来的,它是对总体相关系数p的估计。可以证明,这样计算的样本相关系数是总体相关系数的一致估计。
多个变量之间的线性相关程度,则需要用复相关系数和偏相关系数去度量。
- 相关系数的特点
样本相关系数r的取值范围为-1到1(闭区间)。当r=0时,表示X和Y之间没有线性相关关系。当r的绝对值等于1时,表示X和Y之间完全线性相关。
使用相关系数分析相关关系时应当注意以下几点:
(1)rxy=ryx
(2)相关系数只反映变量间的线性相关程度,不能说明非线性相关关系。
(3)相关系数不能确定变量的因果关系,也不能说明相关关系具体接近于哪条直线。
(4)样本相关系数是根据从总体中抽取的随机样本的观测值Xi和Yi计算出来的,它只是对总体相关系数p的估计。因此样本相关系数不是确定的值,而是随抽样而变动的随机变量。对相关系数的统计显著性还有待进行检验。
(三)回归分析
研究变量相互之间的相关关系时,首先需要分析它们是否存在相关关系,然后要明确其相关关系的类型,而且还应计量其相关关系的密切程度,在统计学中这种研究称为相关关系。相关分析主要是用一个指标(相关系数)去表明现象间相互依存关系的性质和密切程度。不过相关分析并不能说明变量间相互关系的具体形式,也还不能从一个变量的变化去推测另一个变量的具体变化。如果要测定变量之间相关关系的数量形式,还需要运用回归分析的方法。
现代意义的回归是关于一个变量(被解释变量或因变量)对另一个或多个变量(解释变量)依存关系的研究,是用适当的数学模型去近似地表达或估计变量之间地平均变化关系,其目的是要根据解释变量的数值去估计所研究的被解释变量的总体平均值。
例如,研究个人消费支出Y与个人可支配收入X的依存关系,对应于一定的个人可支配收入水平,个人消费支出并不确定,但总是在一定的范围内变动。其关系如下图所示。
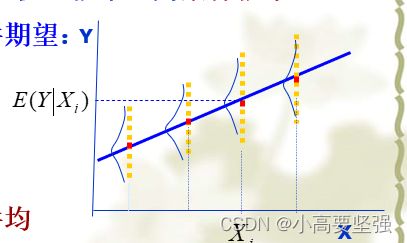
回归分析就是要研究当解释变量个人可支配收入变动时,被解释变量个人消费支出的平均水平变动的规律。
在理解回归分析时,应当注意回归所要揭示的是被解释变量与解释变量之间的平均关系。在这里,被解释变量是随机变量,解释变量在本质上可以是随机变量,但在一般情况下,解释变量是作为非随机变量来处理的。
相关关系与回归分析有密切的联系,他们都是对变量间相关关系的研究,二者可以相互补充。相关分析可以表明变量间相关关系的性质和程度,只有当变量间存在一定程度的相关关系时,进行回归分析去寻求相关的具体数学形式才有实际的意义。同时,在进行相关分析时,要具体确定变量间相关的数学形式,又要依赖于回归分析,而且在多个变量的相关分析中,相关系数的确定也是建立在回归分析基础上的。
相关分析与回归分析的研究目的和研究方法是有明显区别的。从研究目的上看,相关分析是用一定数量指标(相关系数)度量变量间相互联系的方向和程度;回归分析却是要寻求变量间联系的具体数学形式,是根据解释变量的固定值去估计和预测被解释变量的平均值。从对变量的处理看,相关分析不考虑解释变量与被解释变量的因果关系,而回归分析是建立在变量因果关系分析的基础上,研究其中解释变量的变动对被解释变量的具体影响。
经济现象间的本质联系,取决于它们的客观规律性,需要结合实际经验去分析,并要由经济学理论去加以说明。否则,可能会出现“伪回归”,不仅无实际经济意义,而且会导致荒谬的结论。
二、总体回归函数
如果把被解释变量Y的条件期望表示为X的某种函数,可写为
E(Y|Xi)=f(Xi)
如上式,将总体被解释变量Y的条件期望表现为解释变量X的函数,这个函数称为总体回归函数(population regression function,PRF)。该式是总体回归函数的条件均值表示方式。
假如Y的总体条件期望E(Y|Xi)是解释变量X的线性函数,可表示为:

式中,B1和B2是未知的参数;B1是截距系数;B2是斜率系数。
对于一定的Xi,Y的各个个别值Yi并不一定等于条件期望,而是分布在E(Y|Xi)的周围,若令各个Yi与条件期望E(Y|Xi)的偏差为ui,显然ui是个随机变量。即个别值表现形式
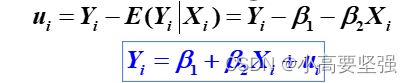
在计量经济学中线性模型的“线性”有两种解释。一是模型就变量而言是线性的,即Y的条件期望E(Y|Xi)是解释变量Xi的线性函数。二是模型就参数而言是现行的,即Y的条件期望E(Y|Xi)是参数B的线性函数,而对于解释变量Xi既可以是线性的,也可以是非线性的。在计量经济学中,从回归理论和参数的估计方法考虑,通常是就参数而言判断是否是线性回归模型,而对解释变量Xi则既可以是线性,也可以是非线性的。
三、随机扰动项u
如果总体回归函数是只有一个解释变量的线性函数,则有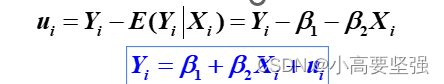
式中表明,除已列入模型的解释变量X以外,还有影响被解释变量Y的其他因素,这里的随机扰动项ui就代表着那些对Y有影响但又未纳入模型的诸多因素的综合影响。
在总体回归函数中引进随机扰动项,主要有以下几方面的原因。
(1)作为未知影响因素的代表。
(2)作为无法取得数据的已知因素的代表。
(3)作为众多细小影响因素的综合代表。
(4)模型的设定误差。
(5)变量的观测误差。
(6)经济现象的内在随机性。
由此可见,随机扰动项具有十分丰富的内容,在计量经济研究中起着重要的作用。对随机扰动项的处理是计量经济分析中的重要内容,在一定程度上,随机扰动项的性质决定着计量经济方法的选择和使用。
四、样本回归函数
对于实际的经济问题,通常总体包含的单位数很多,无法掌握所有单位的数值,总体回归函数实际上是未知的。我们可能做到的只是对应于解释变量X的选定水平,对被解释变量Y的某些样本进行观测,然后通过对样本观测获得的信息去估计总体回归函数。
如果把被解释变量Y的样本条件均值表示为解释变量X的某种函数,这个函数称为样本回归函数(sample regression function,SRF)。显然,样本回归函数的函数形式应与设定的总体回归函数的函数形式一致。样本回归函数如为线性函数,可表示(条件均值形式)为:

式中,Yi估计是回归线上与Xi相对应的Y的样本条件均值,可视为对总体条件期望E(Y|Xi)的估计。
与总体回归函数相类似,实际观测的被解释变量值Yi并不完全等于样本条件均值Yi的估计,二者之差可用ei表示,那么:
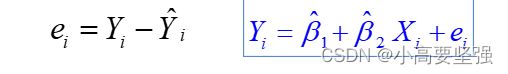
上式为样本回归函数的另一种表达形式(个别值形式),与条件均值形式是等价的,这里的ei称为剩余项,或称为残差。在样本回归函数中引入ei的原因,与将ui引入总体回归函数的理由是相同的。
必须明确,样本回归函数与总体回归函数是有区别的。首先,总体回归函数虽然未知,但它是确定的;而由于从总体中每次抽样都能获得一个样本,就都可以拟合一条样本回归线,所以样本回归线是随抽样波动而变化的,可以有很多条。所以,样本回归线还不是总体回归线,至多只是未知的总体回归线的近似反映。其次,总体回归函数的参数B1和B2是确定的常数;而样本回归函数的参数B1估计和B2估计是随抽样而变化的随机变量。此外,总体回归函数中的ui是不可直接观测;而样本回归函数中的ei是只要估计出样本回归的参数就可以计算的数值。
回归分析的目的是要用样本回归函数去尽可能准确地估计总体回归函数。由于样本对总体总存在代表性误差,SRF又总会过高或过低估计PRF。显然,需要寻求一种规则和方法,使得到地样本回归函数的参数B1估计和B2估计能够“尽可能接近”总体回归函数中的参数B1和B2。这是计量经济学应当解决的参数估计的基本问题。
第二节 简单线性回归模型参数的估计
估计线性回归模型中参数的方法有若干种,这些估计方法都是以对模型的某些假设条件为前提的。因为只有具备这些假定条件,所做出的估计才具有良好的统计性质。所以,这些假定与所采用的估计方法是紧密相关的。
一、简单线性回归的基本假定
对简单线性回归模型的基本假定有两个方面:一是对变量和模型的假定;二是对随机扰动项ui统计分布的假定。
在简单线性回归模型中对变量和模型的假定,首先,假定解释变量Xi是确定型变量,是非随机的,这是因为在重复抽样中Xi是取一组固定的值。或者Xi虽然是随机的,但与随机扰动项ui也是不相关的。其次,假定模型中的变量没有测量误差。此外,还要假设模型对变量和函数形式的设定是正确的,即不存在设定误差。
对随机扰动项ui的分布做出的一些基本假定如下:
(1)零均值假定,E(ui|Xi)=0。
(2)同方差假定。Var(ui|Xi)=o2
(3)无自相关假定,即随机扰动项ui的逐次值互不相关。Cov(ui,uj)=0。(i不等于j)
(4)随机扰动项ui与解释变量Xi不相关,可表示为Cov(ui,Xi)=0。
(5)正态性假定,即假定随机扰动项ui服从期望为0、方差为o2的正态分布。表示为ui~N(0,o2)
这些假设也称为高斯假定或古典假定。满足以上古典假定的线性回归模型,也称为古典线性回归模型。
容易证明,对Yi分布性质的假定与对随机扰动项ui分布的古典假定是等价的。
二、普通最小二乘估计
估计回归模型参数的方法有很多。例如,用产生该样本概率最大的原则去确定样本回归函数,称为极大似然准则;用使估计的剩余平方和最小的原则确定样本回归函数,称为最小二乘准则。本文主要解释古典假定下的最小二乘法,也称为普通最小二乘估计(ordinary least squares estimators,OLS或OLSE)。
使样本回归函数“尽可能接近”总体回归函数,就是要使估计的Yi估计与实际的Yi的误差尽量小,即要是剩余项ei越小越好。而ei有正有负,可采用剩余平方和最小的准则,即

然后分别对各参数求偏导,有

从而得如下方程组:
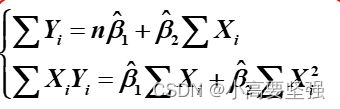
其中,n为样本容量,该方程组称为最小二乘的正规方程组。根据克莱姆法则求解正规方程组,得:

式中,即是用样本观测值Xi和Yi表现的B1估计和B2估计的最小二乘估计量。
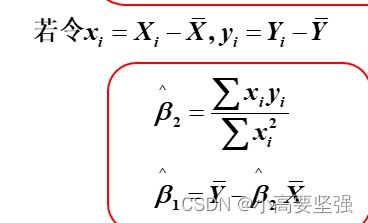
上式是根据最小二乘准则推导出来的,称为简单线性回归模型参数的最小二乘估计量,由这些估计量可直接用样本观测值求得参数的估计值。
三、OLS回归线的性质
用普通最小二乘法拟合的样本回归线有以下性质。
(1)样本回归线通过样本均值。
(2)估计值Yi的估计的均值等于实际值Yi的均值。因为

(3)剩余项ei的均值为零。
(4)被解释变量估计值Yi估计与剩余项ei不相关。
(5)解释变量Xi与剩余项ei不相关。
普通最小二乘法估计的回归线所具有的以上性质,在计量经济方法的估计、检验及一些结论的证明中都会用到,具有重要的意义。
四、最小二乘估计量的统计性质
(一)参数估计量的评价标准
参数估计值是随抽样而变化的随机变量,加之估计方法和假设前提不一定那么完备,用样本估计的参数数值不一定等于总体参数的真实值。那么,在比较不同估计方法的估计结果时,需要有一定的评价标准,这个标准就是应使参数估计值“尽可能接近”总体参数的真实值。
通常选择参数的估计量时应主要考虑以下一些标准。
-
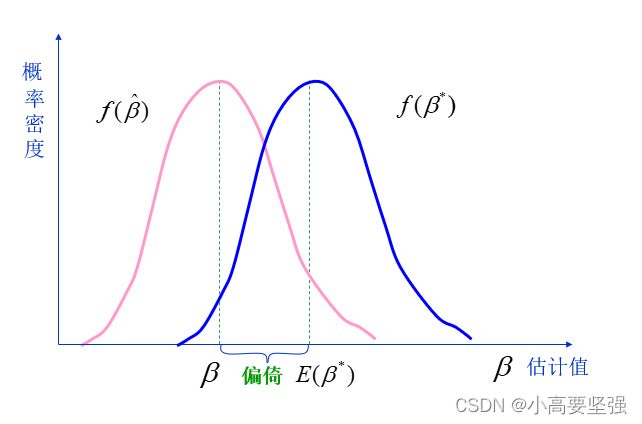
无偏性
如果参数的估计量B的期望等于参数的真实值B,即E(B估计)=B,则称B估计是参数B的无偏估计量。若不等于,则称B估计是有偏的。
-
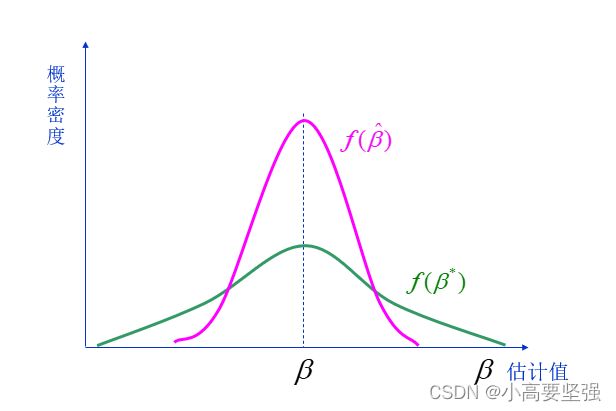
有效性
在计量经济研究中,通常用不同的方法可以获得若干不同的参数估计量,虽然这些估计量可能具有无偏性,但其抽样分布的方差可能不同。一个估计量若不仅具有无偏性而且具有最小方差性,则称这个估计量为有效估计量。
-
一致性
在样本容量较小的情况下,有时很难找到最佳无偏估计量,这时还需要考虑当样本容量充分大或趋于无穷大时估计量的渐进性质。
当样本容量趋于无穷大时,如果估计量B估计的抽样分布依概率收敛于总体参数的真实值B,即

则称估计量B估计为一致估计量。
(二)OLS估计量的统计特性
可以证明,在古典假定完全满足的条件下,回归模型参数的最小二乘估计量具有以下统计性质。
-
线性特性
最小二乘估计B1估计、B2估计是关于Yi的线性函数。(同样也是ui的线性函数)由B1估计、B2估计服从正态分布,Yi是随机变量,服从正态分布。

-
无偏性
E(Bi估计)=Bi,i=1,2
这表明普通最小二乘法估计的参数B1估计和B2估计的期望值等于总体回归函数参数真实值B1和B2,所以OLS估计式是无偏估计量。

-
有效性
为了说明OLS估计式的方差特性,必须导出B1估计和B2估计方差的公式:

可以证明,在总体回归函数参数B1和B2的所有无偏估计量中,普通最小二乘估计B1估计和B2估计具有最小的方差。
在计量经济学中还常用标准误差去度量估计量的精确性,标准误差是方差的平方根,可用SE表示,所以
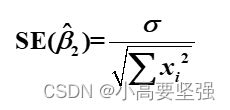
在上面公式中,除了样本观测值以外,都包含了随机扰动项ui的方差,然而它是未知的,所以也需要通过样本去估计。

可证明,上式为随机扰动项方差的无偏估计。n-2为自由度。
- 渐近一致性
注意:OLS估计量B1估计和B2估计之所以具有最佳线性无偏的优良性质,其前提条件是一开始就明确的基本假定都满足,如果这些基本假定不满足,OLS估计量将不一定是最佳线性无偏估计量。
第三节 拟合优度的度量
所估计的样本回归线对样本观测数据拟合的优劣程度,称为样本回归线的拟合优度。在计量经济学中,度量模型拟合优度的可决系数建立在对被解释变量总方差分解的基础之上。
一、总变差的分解
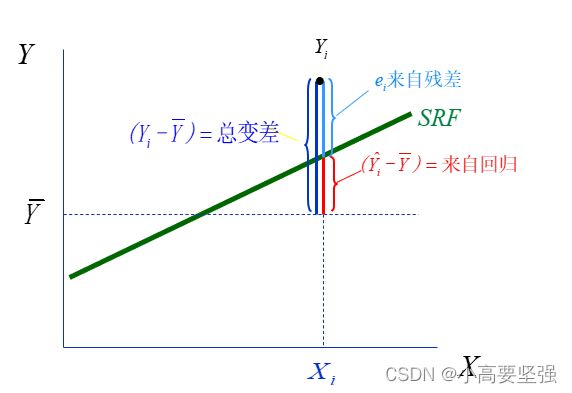
如果以被解释变量平均值为基准,说明被解释变量观测值Yi和估计值Yi估计对被解释变量平均值的偏离程度,上式可用离差表示为

然后左右两边平方并对所有观测值加总,得到:

(1)被解释变量Y的样本观测值与平均值的离差平方和,称为总变差或总离差平方和,用TSS表示。
(2)被解释变量Y的样本估计值与其平均值的离差平方和,称为由回归解释的平方和,是由模型回归线作出解释的变差,用ESS(explained sum of squares)表示。
(3)被解释变量观测值与估计值之差的平方和,是回归线未作出解释的平方和或残差平方和(residual sum of squares),用RSS表示。
其中,TSS = ESS + RSS
二、可决系数
如果样本回归线对样本观测值拟合程度越好,各样本观测点与回归线靠得越近,由样本回归作出解释的离差平方和在总离差平方和中占的比重也将越大,反之拟合程度越差,这部分所占比重就越小。
可决系数(判定系数),在简单线性回归中一般用r2或R2表示,可定义为

可决系数R2有如下特点:
(1)可决系数是非负的统计量。
(2)可决系数的取值范围为[0,1]。
(3)可决系数R2是样本观测值的函数,是随抽样而变动的随机变量。
三、可决系数与相关系数的关系
在一元线性回归中,可决系数R2在数值上是简单线性相关系数r的平方。但是应注意二者在概念上是有明显区别的。
首先,从意义上讲,可决系数R2是就估计的回归模型而言,度量回归模型对样本观测值的拟合程度,也就是模型中解释变量对被解释变量变差的解释程度;相关系数是就两个变量而言,说明两个变量的线性依存程度。其次,可决系数度量的是解释变量与被解释变量不对称的因果关系,是在回归分析的基础上说明X对Y的变差的解释比例,并不说明Y对X的解释。而相关系数r度量的是X与Y对称的相关关系,不涉及X与Y具体的因果关系。而且,可决系数具有非负性;而相关系数可正可负。
第四节 回归系数的假设检验和区间估计
一、OLS估计的分布性质
B1估计、B2估计为随抽样而变化的随机变量,且服从正态分布。

可证明,随机扰动项方差的无偏估计为:

- 若在随机扰动项方差已知时,可构造Bi(i=1,2)参数的Z统计量,为:
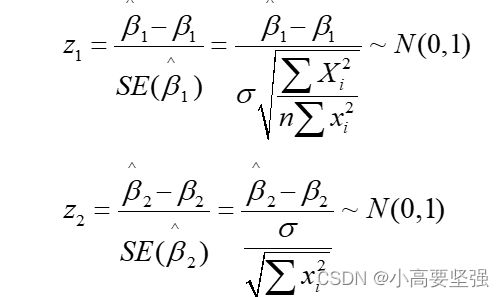
- 若在随机扰动项方差未知时,当样本为大样本时,仍构造Z统计量(根据中心极限定理);当样本为小样本时,可用随机扰动项方差的估计去代替随机扰动项方差,但所得的t统计量不再服从正态分布,而是服从自由度为n-2的t分布:

二、回归系数的假设检验
简单线性回归模型的系数和方差都不能直接观测或准确计算,只能通过样本观测值去估计,所得到的样本回归系数的估计量是随抽样而变动的随机变量。那么,估计的回归系数和方差是否可靠,是否仅仅为抽样的偶然结果,还需要进行统计推断检验(即假设检验)。
为了检验所建立的回归模型中解释变量对被解释变量是否有显著影响,经常把回归系数B2=0作为原假设,B2不等于0为备择假设。随后构建统计量,有两种情况:
- 当随机扰动项方差已知时,或样本充分大时,可根据样本构造Z统计量。给定显著性水平下,查询临界值,比较,进行判断。
- 当随机扰动项方差未知时,且样本容量较小,这是用随机扰动项方差的无偏估计进行替换,构造自由度为n-2的t统计量。给定显著性水平下,查询临界值,比较,进行判断。除此之外,可以利用P值大小与显著性水平a比较进行判断。(小于a,则拒绝原假设)
若拒绝原假设,则认为对应解释变量对被解释变量有显著影响。
三、回归系数的区间估计
区间估计式的意义:在重复抽样之下,像这样的区间构造很多次,平均来说,这样的区间将有1-a的比例是包含参数真实值的。显然,构造参数的置信区间需要先确定参数估计式的抽样分布。
对回归系数的区间估计,可分为以下三种情况:
(2)当总体方差未知,且样本容量充分大时,可用无偏估计去代替。此时由于样本容量充分大,仍可认为
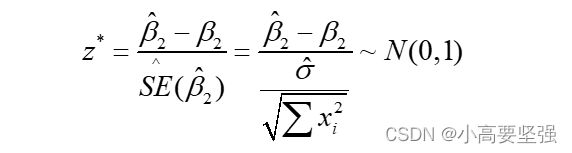
同样可以利用正态分布去确定B2的置信区间。
(3)当总体方差未知时,且样本容量较小时,用总体方差无偏估计去代替,有

这里的统计量t不再服从正态分布,而是服从自由度为n-2的t分布,可利用t分布去建立置信区间。
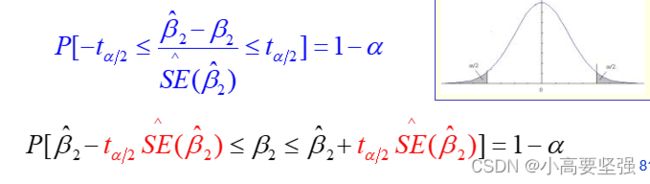
第五节 回归模型的预测
一、被解释变量平均值预测
回归分析的目的之一是对被解释变量作合理的预测。所谓预测,是指由已知的或预先测定的解释变量,去预测被解释变量在所观测的样本数据以外的数值。如果所建立的回归方程通过了各项统计检验,并且在经济上也是有实际意义的,我们估计出参数的回归模型就可以用于对被解释变量的预测。
对被解释变量的预测可分为对被解释变量Y的平均值预测和个别值预测。对Y的平均值预测又分为对平均值的点预测和区间预测。
(一)对Y平均值的点预测
把解释变量的预测值Xf直接代入所估计的样本回归函数,就可以计算出被解释变量平均值的预测值。
(二)对Y平均值的区间预测
为了由预测值Yf估计去对真实平均值E(Yf|Xf)作区间预测,应考虑预测值Yf估计的抽样分布,并寻找与Yf估计与E(Yf|Xf)都有关的统计量。

二、被解释变量个别值预测
关于被解释变量个别值预测,需要明确与预测值Yf估计和个别值Yf都有关的统计量的概率分布。
由前面分析已知,与预测期解释变量对应的残差项ef=Yf-Yf估计,正是与预测值Yf估计和个别值Yf都有关的随机变量,而且在ui服从正态性假定下,ef也服从正态分布,可以证明

随后构造统计量:
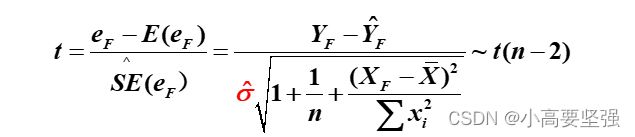
最后给定显著性水平a,置信度为1-a的预测区间为:
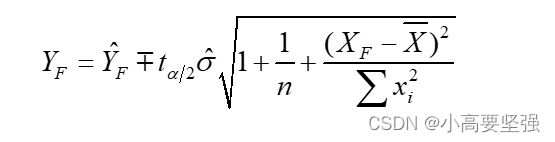
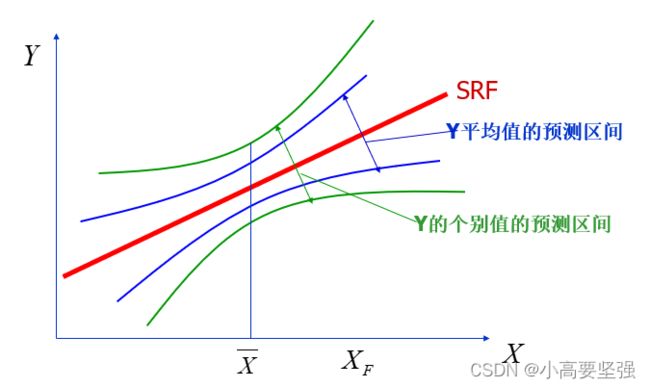
从对被解释变量的平均值预测和个别值预测,可以看出有以下特点:
(1)由于抽样误差的存在,用样本估计的B1估计和B2估计去预测的被解释变量平均值Yf估计与总体真实平均值E(Yf|Xf)存在误差,这主要取决于抽样波动。而用Yf估计对个别值Yf的预测,不仅存在由抽样波动引起的误差,而且要受到随机扰动项ui的影响。对Yf估计个别值预测的方差要大于平均值预测的方差。
(2)对Yf的平均值预测区间和个别值预测区间都不是常数,它们是随解释变量预测值Xf的变化而变化的。当Xf=X平均值时,此时预测区间最窄,所以用回归模型预测时,Xf取值不宜偏离X均值过远,否则预测精度会大大降低。
(3)预测区间与样本容量n有关。当样本容量趋于无穷大时,抽样误差趋于0,此时对平均值的预测误差也趋于0,而对个别值的预测误差只取决于随机扰动ui的方差。
本文主要参考庞皓计量经济学第三版