Python使用OpenCV仿射变换实例

图像img的像素为534*300，img.shape = (300, 534, 3)。

需要引入：

import cv2 as cv
import numpy as np

img.shape得到的(300, 534, 3)，前者300是高度，y轴的值，后者534是宽度，x轴的值，这一点有些不同。

图像的xy轴，是以图像左上角顶点为(0, 0)原点，类似于css。从顶点沿宽度向右是x正轴，沿高度向下是y正轴。

一、平移变换

cv2.warpAffine()   仿射变换（从二维坐标到二维坐标之间的线性变换，且保持二维图形的“平直性”和“平行性”。仿射变换可以通过一系列的原子变换的复合来实现，包括平移，缩放，翻转，旋转和剪切）
    参数：
        img: 图像对象
        M：2*3 transformation matrix (转变矩阵)
        dsize：输出矩阵的大小,注意格式为（cols，rows）  即width对应cols，height对应rows
        flags：可选，插值算法标识符，有默认值INTER_LINEAR，
               如果插值算法为WARP_INVERSE_MAP, warpAffine函数使用如下矩阵进行图像转dst(x,y)=src(M11*x+M12*y+M13,M21*x+M22*y+M23)
        borderMode：可选， 边界像素模式，有默认值BORDER_CONSTANT 
        borderValue:可选，边界取值，有默认值Scalar()即0

下面的M矩阵表示向x轴正方向（向右）移动200像素，向y轴负方向（向上）移动100像素。

# 创建转变矩阵
M = np.float32([[1, 0, 200], [0, 1, -100]])
# 使用warpAffine()方法执行变换
img = cv.warpAffine(img, M, (500, 300))
# 展示图片
cv.imshow("img", img)
cv.waitKey(0)

二、缩放变换

缩放变换的转变矩阵与平移变换的转变矩阵是一样的。

M是一个2*3矩阵，[[1, 0, 100], [0, 1, 200]]。

从左到右看，第一个“1”代表x轴（长度）是原来的几倍，“100”表示将原图沿x轴如何移动。

第二个“1”表示y轴（宽度）是原来的几倍，“100”表示将原图沿y轴如何移动。

下面的操作表示将原图放大1.5倍。

# 创建转变矩阵
M = np.float32([[1.5, 0, 0], [0, 1.5, 0]])
# 执行变换，输出图片大小为500*400
img = cv.warpAffine(img, M, (500, 400))
# 展示图片
cv.imshow("img", img)
cv.waitKey(0)

三、旋转变换

通过getRotationMatrix2D()能得到转变矩阵M。

　cv2.getRotationMatrix2D()  返回2*3的转变矩阵（浮点型）
    参数：
        center：旋转的中心点坐标
        angle：旋转角度，单位为度数，证书表示逆时针旋转
        scale：同方向的放大倍数

我们以图片的左上角（0，0）原点为旋转中心，旋转30°。

# 创建旋转转变矩阵
M = cv.getRotationMatrix2D((0, 0), 30, 1)
# 执行转变
img = cv.warpAffine(img, M, (500, 300))

cv.imshow("img", img)
cv.waitKey(0)

四、三点定位，仿射变换矩阵的计算，cv2.getAffineTransform()

通过图片变换前后的三组坐标定位，和cv2.getAffineTransform()方法，可以计算出我们需要的仿射变换矩阵M。

该方法可以一定程度上代替上面三个方法，同时实现旋转、平移和缩放。

getAffineTransform()等同于将平移，旋转和缩放的变换矩阵相乘，最后都会获得仿射变换矩阵。

cv2.getAffineTransform()  返回2*3的转变矩阵
    　 参数：
       　　 src：原图像中的三组坐标，如np.float32([[50,50],[200,50],[50,200]])
        　　dst: 转换后的对应三组坐标，如np.float32([[10,100],[200,50],[100,250]])

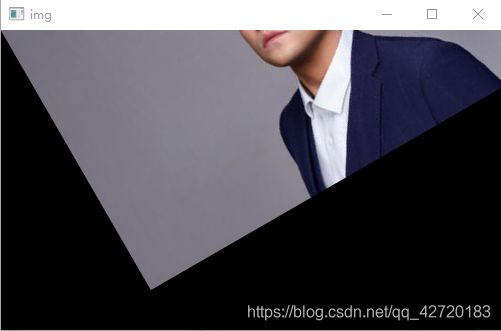
img原图的四个角的坐标为[0, 0] , [534, 0], [0,300], [534, 300]。（此处为[x, y] 坐标形式，不同于shape）

# 原图像中的三组坐标
pts1 = np.float32([[0, 0] , [534, 0], [534, 300]])
# 转换后的三组对应坐标
pts2 = np.float32([[300, 0], [300, 534], [0, 534]])
# 计算仿射变换矩阵
M = cv.getAffineTransform(pts1, pts2)
# 执行变换
img = cv.warpAffine(img, M ,(300, 534))

二维仿射变换总结：我们可以发现，上面的所有仿射变换矩阵M都是一个2*3的矩阵，而用来进行变换的方法都是同一个cv2.warpAffine()。

下面是三维仿射变换

五、透视变换（三维）

与四、三点定位，仿射变换矩阵的计算类似，三维的仿射变换矩阵需要四组坐标来进行定位。

与之前不同的是，我们需要使用另外两个方法getPerspectiveTransform()和warpPerspective()，仿射变换矩阵M变成了3*3矩阵。

cv2.getPerspectiveTransform()   返回3*3的转变矩阵
        参数：    
            src：原图像中的四组坐标，如 np.float32([[56,65],[368,52],[28,387],[389,390]])
            dst: 转换后的对应四组坐标，如np.float32([[0,0],[300,0],[0,300],[300,300]])

            
        cv2.warpPerspective()
        参数：    
            src: 图像对象
            M：3*3 transformation matrix (转变矩阵)
            dsize：输出矩阵的大小，注意格式为（cols，rows）  即width对应cols，height对应rows
            flags：可选，插值算法标识符，有默认值INTER_LINEAR，
                   如果插值算法为WARP_INVERSE_MAP, warpAffine函数使用如下矩阵进行图像转dst(x,y)=src(M11*x+M12*y+M13,M21*x+M22*y+M23)
            borderMode：可选， 边界像素模式，有默认值BORDER_CONSTANT 
            borderValue:可选，边界取值，有默认值Scalar()即0

我们将img图片的左上角和右上角往“里”缩一缩，同时左下角和右下角位置不变。

# 原图的四组顶点坐标
pts3D1 = np.float32([[0, 0], [534, 0], [0, 300], [534, 300]])
# 转换后的四组坐标
pts3D2 = np.float32([[100, 100], [434, 100], [0, 300], [534, 300]])
# 计算透视放射矩阵
M = cv.getPerspectiveTransform(pts3D1, pts3D2)
# 执行变换
img = cv.warpPerspective(img, M, (550， 400))