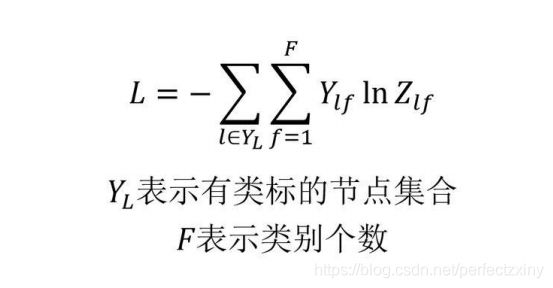GCN网路详解

GCN原理

1 邻接矩阵: A是图的邻接矩阵

2 特征矩阵 设 A 是n阶方阵，如果存在数m和非零n维列向量x，使得 Ax=mx 成立，则称 m 是矩阵A的一个特征值（characteristic value)或本征值（eigenvalue)。
3 度矩阵 D 是顶点的度矩阵（对角矩阵），对角线上元素依次为各个顶点的度，

4 拉普拉斯矩阵

对于图[G=(V,E)其Laplacian 矩阵的定义为L=D-A 其中L是Laplacian矩阵，D是顶点的度矩阵（对角矩阵），对角线上元素依次为各个顶点的度，A是图的邻接矩阵。看图5的示例，就能很快知道Laplacian 矩阵的计算方法。

图5 Laplacian 矩阵的计算方法

为什么GCN要用拉普拉斯矩阵？

拉普拉斯矩阵矩阵有很多良好的性质，这里写三点我感触到的和GCN有关之处

• 拉普拉斯矩阵是对称矩阵，可以进行特征分解（谱分解），这就和GCN的spectral domain对应上了
• 拉普拉斯矩阵只在中心顶点和一阶相连（就是直接相连）的顶点上（1-hop neighbor）有非0元素，其余之处均为0
• 通过拉普拉斯算子与拉普拉斯矩阵进行类比（详见第6节）

superbrother 拉普拉斯矩阵与拉普拉斯算子的关系

GCN的核心基于拉普拉斯矩阵的谱分解。

矩阵的谱分解，特征分解，对角化都是同一个概念
不是所有的矩阵都可以特征分解，其充要条件为n阶方阵存在n个线性无关的特征向量]

但是拉普拉斯矩阵都是半正定对称矩阵（半正定矩阵本身就是对称矩阵，此处这样写为了和下面的性质对应，避免混淆），有如下三个性质：

• 对称矩阵一定有n个线性无关的特征向量
• 半正定矩阵的特征值一定非负
• 对称矩阵的特征向量相互正交，即所有特征向量构成的矩阵为正交矩阵

5.图卷积神经网络网络 GCN
图卷积神经网络网络 Graph Convolutional Network (GCN) 最早是在 2016 年提
出，2017 年发表在 ICLR 上。GCN 主要是将卷积操作应用到图结构上，如下图所示，
GCN 输入的 chanel 为 C (即节点 Xi 特征向量的维度)，GCN 输出的 chanel 为 F，
即每个节点 (Zi) 的特征向量维度为 F，最后用节点的特征对节点进行分类预测等：

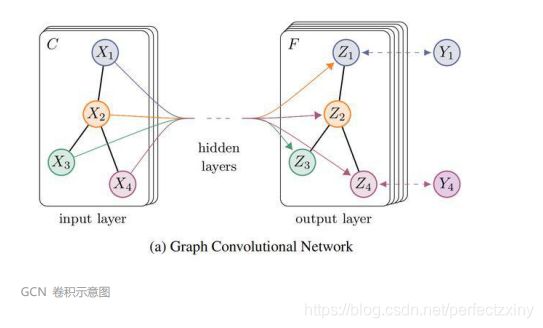
GCN 卷积示意图

GCN 和 CNN 类似，具有强大的特征学习能力，它们的实质也是类似的，某个点的卷
积可以看成对该点邻居的加权求和。下图为传统的图像 (image) 卷积操作，每个点表
示一个像素，图像的像素也可以看成是一种图 (graph) 结构，相邻的像素之间有边连
接，而卷积是对像素邻居进行加权平均得到的。

图像 (image) 的二维卷积
而对于图 (graph) 结构，也可以采取类似的方法进行卷积。例如对下图中红色的节点
卷积就等于取其邻居节点进行加权平均。
图 (graph) 结构卷积

GCN 中给出了图卷积的计算公式，如下所示，其中 H(l) 表示节点在第 l 层的特征向
量，H(l+1) 表示经过卷积后节点在第 l+1 层的特征向量，W(l) 表示第 l 层卷积的参
数，σ 表示激活函数。而由矩阵 A、D 组成的部分是一种拉普拉斯矩阵 (Laplacian
matrix)，A+I 中的 I 为单位矩阵，即对角线为 1，其他为 0 的矩阵：

GCN 卷积公式

GCN卷积公式的理解：

对图像 (image) 中某一个像素进行卷积实际上是对该像素及相邻像素进行加权求和，
那么在图 (graph) 结构中对某一个节点卷积就应该是对该节点和其邻居节点进行加权
求和。
我们首先考虑最简单的图卷积操作，如下公式：

简单的图卷积公式
上面的公式中 W 为卷积变换的参数，可以训练优化。A 矩阵为邻接矩阵，Aij 不为 0 则
表示节点 i，j 为邻居。H 为所有节点的特征向量矩阵，每一行是一个节点的特征向量，
H(0) 就是 X 矩阵。A 和 H 的乘积其实就是把所有的邻居节点向量进行相加，如下所
示。

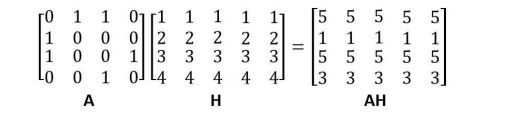
矩阵 A 和 H 相乘

上式的邻接矩阵中，节点 1 和节点 2、3 为邻居，则 A 乘上 H 后节点 1 的特征向量
就用节点 2、3 特征向量加和得到，即 [2,2,2,2,2]+[3,3,3,3,3]=[5,5,5,5,5]。得到 AH 之
后再和 W 相乘，最后经过激活函数 σ 就得到下一层节点的特征向量了。
但是上面的公式存在一些问题，AH 只获得了某个节点的邻居信息，而忽略了节点本身
信息。为了解决这个问题，我们可以将矩阵 A 中对角线的值设为 1，即每个节点会指
向自身，新的卷积公式如下：

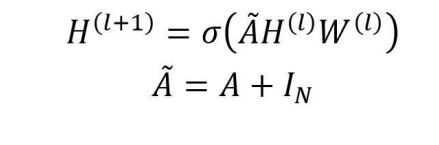
I 为单位矩阵，即对角线为 1，其余为 0。使用上面的卷积公式即可把节点自身的信息
也考虑进去，但是这个公式仍然存在问题：矩阵 A 没有归一化，AH 会把节点所有邻
居的向量都相加，这样经过多层卷积后向量的值会很大。
因此需要对矩阵 A 进行归一化，归一化要用到图的度矩阵 D，可以直接使用矩阵 D 的
逆和 A 相乘，如下：

邻接矩阵归一化
但是上面的归一化公式得到的 A 不是对称矩阵，通常使用对称归一化的方法：
邻接矩阵对称归一化
把上面的优化方法结合在一起，就是 GCN 的卷积公式了：

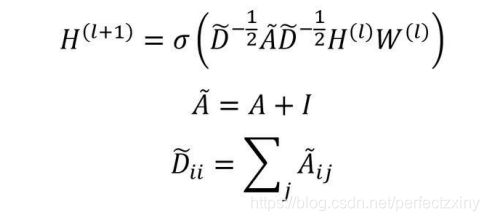
6.GCN 预测
GCN 可以用最后一层卷积层得到的节点特征向量进行预测，假设 GCN 只有两层，则
预测的公式如下：

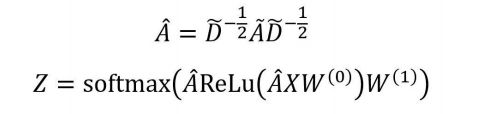
分类的损失函数如下：