2020-4-17 深度学习笔记20 - 深度生成模型 1 (玻尔兹曼机,受限玻尔兹曼机RBM)
第二十章 深度生成模型 Deep Generative Models
中文
英文
深度生产模型在某种程度上都代表了多个变量的概率分布。
从数据分布生成真实样本是生成模型的目标之一。
有些模型允许显式地计算概率分布函数。 其他模型则不允许直接评估概率分布函数,但支持隐式获取分布知识的操作,如从分布中采样。
为了让模型理解表示在给定训练数据中的大千世界,训练具有隐藏单元的生成模型是一种有力方法。 通过学习模型 p model ( x ) p_{\text{model}}(x) pmodel(x)和表示 p model ( h ∣ x ) p_{\text{model}}(h \mid x) pmodel(h∣x),生成模型可以解答 x x x输入变量之间关系的许多推断问题, 并且可以在层次的不同层对 h h h求期望来提供表示 x x x的许多不同方式。 生成模型承诺为AI系统提供它们需要理解的、所有不同直观概念的框架,让它们有能力在面对不确定性的情况下推理这些概念。
玻尔兹曼机Boltzmann machine
玻尔兹曼机(Boltzmann machine)最初用来学习二值向量上的任意概率分布。
玻尔兹曼机的变体(包含其他类型的变量)早已超过了原始玻尔兹曼机的流行程度。
我们在 d d d维二值随机向量 x ∈ 0 , 1 d x \in {0, 1}^d x∈0,1d上定义玻尔兹曼机。 玻尔兹曼机是一种基于能量的模型,意味着我们可以使用能量函数定义联合概率分布:
P ( x ) = exp ( − E ( x ) ) Z P(x) = \frac{\exp(-E(x))}{Z} P(x)=Zexp(−E(x))
其中 E ( x ) E(x) E(x)是能量函数, Z Z Z是确保 ∑ x P ( x ) = 1 \sum_{x} P(x)=1 ∑xP(x)=1的配分函数。
玻尔兹曼机的能量函数如下 给出:
E ( x ) = − x ⊤ U x − b ⊤ x E(x) = -x^\top U x - b^\top x E(x)=−x⊤Ux−b⊤x
其中 U U U是模型参数的”权重”矩阵, b b b是偏置向量。
这意味着一个单元的概率由其他单元值的线性模型(逻辑回归)给出。
正式地,我们将单元 x x x分解为两个子集:可见单元 v v v和潜在(或隐藏)单元 h h h。 能量函数变为
E ( v , h ) = − v ⊤ R v − v ⊤ W h − h ⊤ S h − b ⊤ v − c ⊤ h E(v,h)=−v^⊤Rv−v^⊤Wh−h^⊤Sh−b^⊤v−c^⊤h E(v,h)=−v⊤Rv−v⊤Wh−h⊤Sh−b⊤v−c⊤h
玻尔兹曼机的学习,玻尔兹曼机的学习算法通常基于最大似然。 所有玻尔兹曼机都具有难以处理的配分函数,因此最大似然梯度必须使用第十八章中的技术来近似。
玻尔兹曼机有一个有趣的性质,当基于最大似然的学习规则训练时,连接两个单元的特定权重的更新仅取决于这两个单元在不同分布下收集的统计信息:$ P model ( v ) P_{\text{model}}(v) Pmodel(v)和 P ^ data ( v ) P model ( h ∣ v ) \hat{P}{\text{data}}(v) P{\text{model}}(h \mid v) P^data(v)Pmodel(h∣v)。
这意味着学习规则是”局部”的,这使得玻尔兹曼机的学习似乎在某种程度上是生物学合理的。
受限玻尔兹曼机Restricted Boltzmann Machines
Invented under the name harmonium , restricted Boltzmann machines are some of the most common building blocks of deep probabilistic models.
受限玻尔兹曼机以簧风琴之名面世之后,成为了深度概率模型中最常见的组件之一。
RBM是包含一层可观察变量和单层潜变量的无向概率图模型。 RBM可以堆叠起来(一个在另一个的顶部)形成更深的模型。
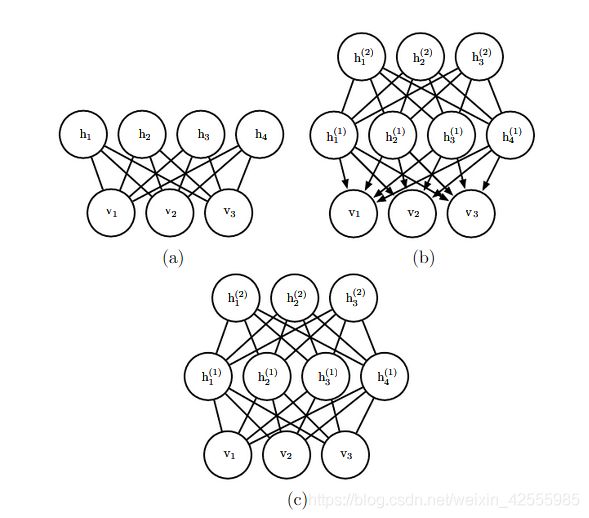
上图是可以用受限玻尔兹曼机构建的模型示例。
- a图:受限玻尔兹曼机本身是基于二分图的无向图模型,在图的一部分具有可见单元,另一部分具有隐藏单元。可见单元之间没有连接,隐藏单元之间也没有任何连接。通常每个可见单元连接到每个隐藏单元,但也可以构造稀疏连接的RBM,如卷积RBM。
- b图:深度信念网络(deep belief network,DBN)是涉及有向和无向连接的混合图模型。与RBM一样,它也没有层内连接。然而,DBN具有多个隐藏层,因此隐藏单元之间的连接在分开的层中。深度信念网络所需的所有局部条件概率分布都直接复制RBM的局部条件概率分布。或者,我们也可以用完全无向图表示深度信念网络,但是它需要层内连接来捕获父节点间的依赖关系。
- c图:深度玻尔兹曼机( deep Boltzmann machine,DBM)是具有几层潜变量的无向图模型。与RBM和DBN一样,DBM也缺少层内连接。DBM与RBM的联系不如DBN紧密。当从RBM堆栈初始化DBM时,有必要对RBM的参数稍作修改。某些种类的DBM可以直接训练,而不用先训练一组RBM。
受限玻尔兹曼机也是基于能量的模型,其联合概率分布由能量函数指定:
P ( v = v , h = h ) = 1 Z e x p ( − E ( v , h ) ) P(v=v,h=h)=\frac1Zexp(−E(v,h)) P(v=v,h=h)=Z1exp(−E(v,h))
RBM的能量函数
E ( v , h ) = − b ⊤ v − c ⊤ h − v ⊤ W h E(v, h) = -b^\top v - c^\top h - v^\top W h E(v,h)=−b⊤v−c⊤h−v⊤Wh
其中 Z Z Z是被称为配分函数的归一化常数: Z = ∑ v ∑ h e x p − E ( v , h ) Z=\sum_v\sum_hexp−E(v,h) Z=∑v∑hexp−E(v,h)
在受限玻尔兹曼机的情况下, 分函数 Z Z Z是难解的。 难解的配分函数 Z Z Z意味着归一化联合概率分布 P ( v ) P(v) P(v)也难以评估。
条件分布
虽然 P ( v ) P(v) P(v)难解,但RBM的二分图结构具有非常特殊的性质,其条件分布 P ( h ∣ v ) P(h \mid v) P(h∣v)和 P ( v ∣ h ) P(v \mid h) P(v∣h)是因子的,并且计算和采样是相对简单的。
我们可以将关于隐藏层的完全条件分布表达为因子形式:
P ( h ∣ v ) = ∏ j = 1 n h σ ( ( 2 h − 1 ) ⊙ ( c + W ⊤ v ) ) j P(h∣v)=\prod_{j=1}^{n_h}σ((2h−1)⊙(c+W^⊤v))_j P(h∣v)=j=1∏nhσ((2h−1)⊙(c+W⊤v))j
类似的推导将显示我们感兴趣的另一条件分布, P ( v ∣ h ) P(v \mid h) P(v∣h)也是因子形式的分布:
P ( v ∣ h ) = ∏ i = 1 n v σ ( ( 2 v − 1 ) ⊙ ( b + W h ) ) i P(v∣h)=\prod_{i=1}^{n_v}σ((2v−1)⊙(b+Wh))_i P(v∣h)=i=1∏nvσ((2v−1)⊙(b+Wh))i
训练受限玻尔兹曼机
因为RBM允许高效计算 P ~ ( v ) \tilde{P}(v) P~(v)的估计和微分,并且还允许高效地(以块吉布斯采样的形式)进行MCMC采样,所以我们很容易使用第十八章中训练具有难以计算配分函数的模型的技术来训练RBM。 这包括CD、SML(PCD)、比率匹配等。
与深度学习中使用的其他无向模型相比,RBM可以相对直接地训练,因为我们可以以闭解形式计算 P ( h ∣ v ) P(h \mid v) P(h∣v)。 其他一些深度模型,如深度玻尔兹曼机,同时具备难处理的配分函数和难以推断的难题。