【现代密码学原理】——传统加密技术(期末复习专享)
前言:传统密码有着悠久的历史。虽然这些密码大都比较简单,现在已经很少采用了,但是研究这些密码的原理,对于理解、构造和分析现代密码都是十分有益的。
目录
- 0. 思维导图
- 1. 传统加密技术
- 2. 对称密码模型
-
- 2.1 密码编码学的特征
- 2.2 密码分析学和穷举攻击
- 2.3 密码分析学常见攻击类型
-
- 2.3.1 唯密文攻击
- 2.3.2 已知明文攻击
- 2.3.3 选择明文攻击
- 2.4 加密算法的选择
- 3. 代替技术
-
- 3.1 Caesar密码
-
- 3.1.1 加密
- 3.1.2 解密
- 3.1.3 攻击
- 3.2 单表代替密码
-
- 3.2.1 加密
- 3.2.2 攻击
- 3.3 多字母代替密码(Playfair密码)
-
- 3.3.1 加密
- 3.3.2 攻击
- 3.4 多表代替加密(Vigenère密码)
-
- 3.4.1 加密
- 3.4.2 解密
- 3.4.3 攻击
- 3.5 多表代替加密(Vernam密码)
-
- 3.5.1 加密
- 3.5.2 解密
- 3.6 一次一密
- 4. 置换技术
-
- 4.1 栅栏技术
- 4.2 矩阵块
- 5. 多层加密
-
- 5.1 转轮机
-
- 5.1.1 加密
- 5.1.2 攻击
- 6. 中英文对照表
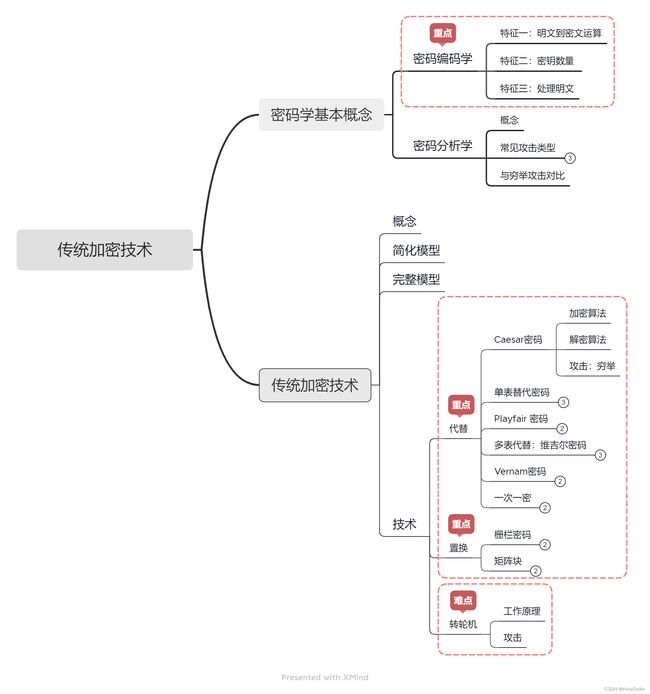
0. 思维导图
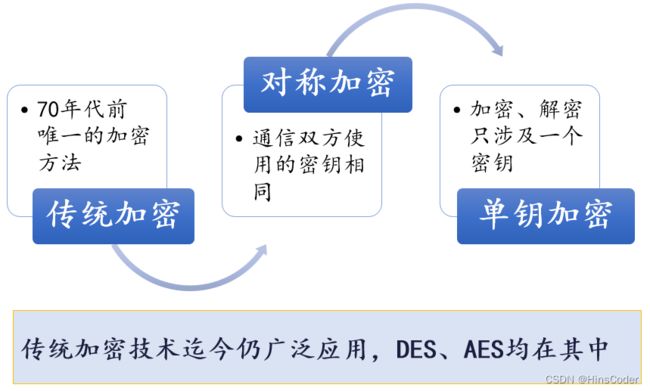
1. 传统加密技术
- 密码编码学:研究各种加密方案的领域
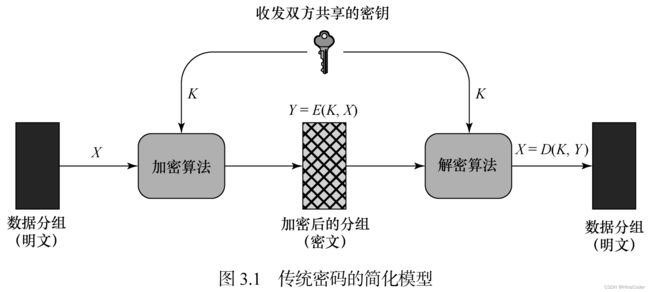
2. 对称密码模型
对称密码方案有5个基本成分:
- 明文:可理解的原始消息或数据,是算法的输入
- 加密算法:加密算法对明文进行各种代替和变换
- 密钥:密钥也是加密算法的输入。密钥独立于明文和算法。算法根据所用的特定密钥而产生不同的输出。算法所用的确切代替和变换也依靠密钥。
- 密文:作为算法的输出,看起来完全随机而杂乱的消息,依赖于明文和密钥。对于给定的消息,不同的密钥产生不同的密文,密文看上去是随机的数据流,并且其意义是不可理解的。
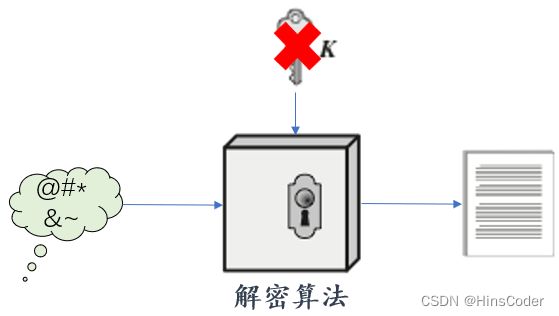
- 解密算法:本质上是加密算法的
逆运算。输入密文和密钥,输出原始明文
安全前提:
-
加密算法足够强
-
密钥安全
问题
- 加密算法公开,使得密码体制的安全性全压在了密钥上
保证密钥的安全成为重中之重
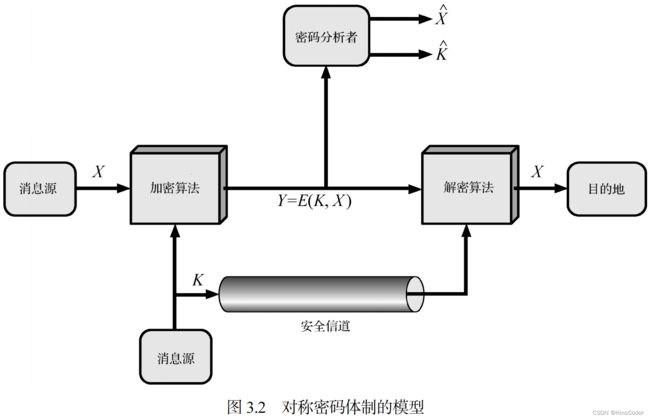
传统密码的完整模型 我们假设基于已知密文和已知加密/解密算法而破译消息是不实际的。换句话说,我们并不需要算法保密,而只需
密钥保密。对称密码的这些特点使得其应用非常广泛。算法不需要保密这一事实使得制造商可以开发出低成本的芯片来实现数据加密算法。这些芯片能够被广泛地使用,许多产品中都有这种芯片。采用对称密码,首要的安全问题是密钥地保密性。
例如,发送方生成明文消息 X = [ X 1 , X 2 , . . . , X M ] X= [ X_1,X_2,...,X_M] X=[X1,X2,...,XM] 的M个元素是某个字母表中的字母。一般来说,字母表由26个大写字母组成。今天,最常用的是二进制字母表{0,1}。加密时,首先生成一个形如 K = [ K 1 , K 2 , . . . , K J ] K= [ K_1,K_2,...,K_J] K=[K1,K2,...,KJ] 的密钥。如果密钥由信息的发送方生成,那么它要通过某种安全信道发送到接受方;另一种方法是第三方生成密钥,然后安全地分发给发送方和接受方。
加密算法根据输入信息X和密钥K生成密文 Y = [ Y 1 , Y 2 , . . . , Y N ] Y= [ Y_1,Y_2,...,Y_N] Y=[Y1,Y2,...,YN] 即
Y = E ( K , X ) Y=E(K,X) Y=E(K,X)
该式表明密文Y是用加密算法E生成的,后者是明文X的函数,而具体的函数由密钥K的值决定。拥有密钥K的预定接收方,可以由变换 X = D ( K , Y ) X=D(K,Y) X=D(K,Y) 得到明文。
假设某敌手窃得Y但不知道K或X,并企图得到K或X,或K和X。假设他知道加密算法E和解密算法D,若他只对这个特定得信息感兴趣,则他会将注意力集中于计算明文得估计值 X ^ {\hat{X}} X^来恢复X;不过,敌手往往对进一步得信息同样感兴趣,此时他企图通过计算密钥得估计值 K ^ \hat{K} K^来恢复K。
2.1 密码编码学的特征
- 明文到密文的运算
所有的加密算法都基于两个原理:
- 代替:将明文中的每个元素映射成另一个元素,但顺序不变,如摩斯电码用—表示0
- 置换:将明文中的元素重新排列,明文字母保存不变,如栅栏技术
⌛ 大多数密码体制都是这两者的多重组合
- 所用的密钥数
-
相同密钥:通信双方使用相同的密钥,这种称为单钥密码、
对称密码、传统密码,如DES、AES -
不同密钥:通信双方使用不同的密钥,这种称为双钥密码、
非对称密码、公钥密码,如RSA
- 处理明文
-
分组密码:加密算法
一次处理一组元素,输出一组元素。(类似并行) -
流密码:加密算法
连续不断的处理元素,但一次只能处理一个元素,输出一个元素。(类似串行)
2.2 密码分析学和穷举攻击
- 密码分析学:利用算法的性质、明文的一般特征或某些明密文对。在缺少某些加密的细节情况下来
推导特定的明文或使用的密钥, - 穷举攻击:对一条密文
尝试所有可能的密钥,直到把它转换为可读的、有意义的明文。平均而言,获得成功至少需要尝试所有可能密钥的一半。密钥的N种可能建立在已知明文类型的基础上
无论哪种方式,一旦推导出密钥,影响都将是灾难性的,过去、现在、未来所有使用该密钥加密的信息内容都出现了非授权泄露。
2.3 密码分析学常见攻击类型
|
|
|
|---|---|
| 唯密文攻击 |
|
| 已知明文攻击 |
|
| 选择明文攻击 |
|
| 选择密文攻击 |
|
| 选择文本攻击 |
|
2.3.1 唯密文攻击
- 【已知解密算法D、密文Y】
运用各种统计方法,对密文本身进行分析。如中文出现频率最高的 “了” ,可查看密文出现频率最高的连续字符串,试着找出映射
2.3.2 已知明文攻击
- 【可能词攻击】
当破译的文件来自特定领域,如腾讯某程序源代码,那么第一行代码必然是公司版权信息 “@TENCENT”。通过这样的方式,人为创造出已知明文及对应密文,从而分析使用的密钥K。
2.3.3 选择明文攻击
- 【已知加密算法E、密文Y】
攻击者通过某种方式控制了发送方主机,在发送的信息中插入一段由他选择的明文信息,如“123”。与此同时截获“123”对应的密文,恢复出密钥K。
上表中还列举了另外两种攻击方法:选择密文攻击和选择文本攻击。它们在密码分析技术中很少用到,但仍然是两种可能的攻击方法,
只有相对较弱的算法才无法抵御唯密文攻击。一般来说,加密算法至少要能经受住已知明文攻击。
2.4 加密算法的选择
- 一次一密 (绝对安全的加密算法)
每加密一次,使用一个新的密钥
使得密文规律被打破,无法推导出密钥
- 计算上安全的加密算法(二者满足其一即可)
- 破译密码的
代价超出密文信息的价值 - 破译密码的
时间超出密文信息的有效生命期
3. 代替技术
- 代替技术是将明文字母替换成其他字母、数字或符号的方法;
- 若将明文看成是二进制序列,则代替就是用密文位串来代替明文位串。
3.1 Caesar密码
- Caesar密码是最早的一种代替密码
- 由古罗马军事统帅Julius Caesar发明,用于在军队中传递加密信息
Ceasar密码的加密原理非常简单,就是对字母表中的每个字母用它之后的第N个字母来代替,例如取3;
如字母a,后面紧随b、c、d,用D代替a;
而字母y,后面紧随z、a、b,用B代替y。
3.1.1 加密

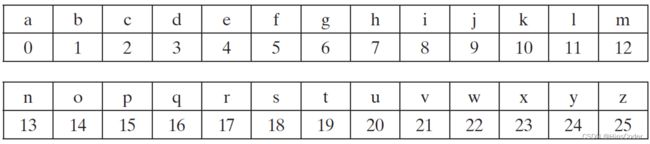
对于明文字母a,密文替换为D,对应值增加了3,即密文=明文+3;
对于明文字母y,密文=24+3=27,而y替换为B(值为1),即27与1等价,只需27 mod(26)= 1
密文 = (明文+3) mod(26)
对每个明文字母x,代替成密文字母Y:
Y = ( x + 3 ) m o d ( 26 ) = E ( 3 , x ) Y = (x+3) mod(26) = E(3,x) Y=(x+3)mod(26)=E(3,x)
即【明文x】以及【数字3】,通过【mod26下的加法运算】这个变换,转变成为密文Y
这个变换就是加密算法E,3是参与运算的密钥k
推广到一般
Y = ( x + k ) m o d ( 26 ) = E ( 3 , x ) Y = (x+k) mod(26) = E(3,x) Y=(x+k)mod(26)=E(3,x)
后面第k个字母来代替原字母,即一般Caesar算法,这里k的取值范围为1到25
3.1.2 解密

对每个密文字母Y,还原成明文字母x:
x = ( Y − 3 ) m o d ( 26 ) = D ( 3 , Y ) x = (Y-3) mod(26) = D(3,Y) x=(Y−3)mod(26)=D(3,Y)
即【密文Y】以及【数字3】,通过【mod26下的减法运算】这个变换,转变成为明文X
这个变换就是解密算法D,3是参与运算的密钥k
推广到一般
x = ( Y − k ) m o d ( 26 ) = D ( k , Y ) x = (Y-k) mod(26) = D(k,Y) x=(Y−k)mod(26)=D(k,Y)
即一般Caesar算法的逆运算,K的取值范围为1到25
练习题
截获密文“IBQQZ FOEJOH”,已知使用Caesar加密,请恢复出明文。
【提示】密钥k在[1,3]之间
3.1.3 攻击
密文: PHHW PH DIWHV WKH WRJD SDUWB
明文: ?
若截获到一个用Caesar密码来加密的密文,那么参与加密运算E的密钥K只有25种可能
数量级很小,可以使用穷举攻击试出密钥K
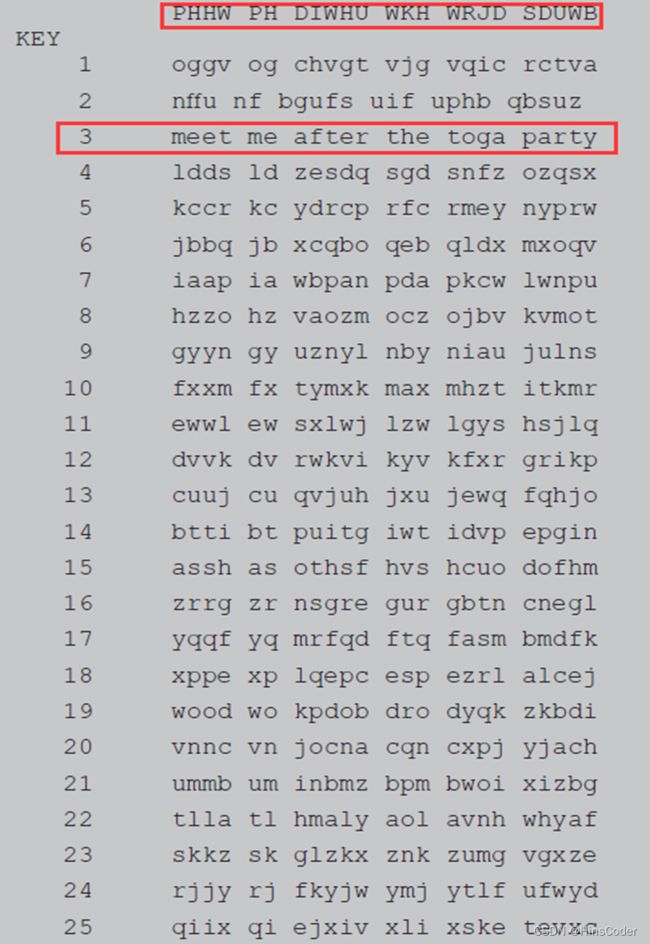
为什么能穷举攻击?
- 已知使用的Caesar密码,即加密算法和解密算法已知
- 密钥一共只有25种可能
- 明文语言已知,语法意义易于识别
如果明文所用的语言不为我们所知,那么明文输出就不可识别。而且,输入可能已按某种方式缩写或压缩,于是就更不可识别。

通信双方发送的是ZIP压缩文件,构成明文的字符没有任何语法意义
尽管使用是简单的代替密码如Caesar密码来进行加密,哪怕攻击者当前测试的就是正确密钥K,也无法判断出这就是明文
3.2 单表代替密码
由于Caesar密码仅有25种可能的密钥,是远远不够安全的。通过允许任意代替,密钥空间将会急剧增大。
我们先定义术语置换
- 有限元素的集合S的置换是S中的所有元素的有序排列,且每个元素只出现一次
- 如集合S ={a,b,c},则S有6个置换 abc, acb, bac, bca, cab, cba
若集合S 由n个元素组成,对S内的n个元素进行全排列
□□…□□□
第1位有n种选择,第2位有n-1种…以此类推,第n-1位有2种选择,第n位有1种选择,一共有n*(n-1)*(n-2)*.......*3*2*1种,即n!
即【明文字母表X】,通过指定【序号K】的【全排列】的变换,生成密文字母表Y
密钥K有26!种可能,远大于Caesar密码的密钥数量,可以抵挡对密钥K的穷举攻击
3.2.1 加密
【明文字母表X】通过指定【序号K】的【全排列】的变换,生成密文字母表Y
全排列这个变换就是加密算法E,指定的序号就是密钥K,Y = E(K,X)
获取明密文字母表映射后,即可为消息加密
3.2.2 攻击
待分析的密文:

【问题】截获密文Y如上,已知使用单表代替加密,如何发起攻击,恢复出原始明文呢?
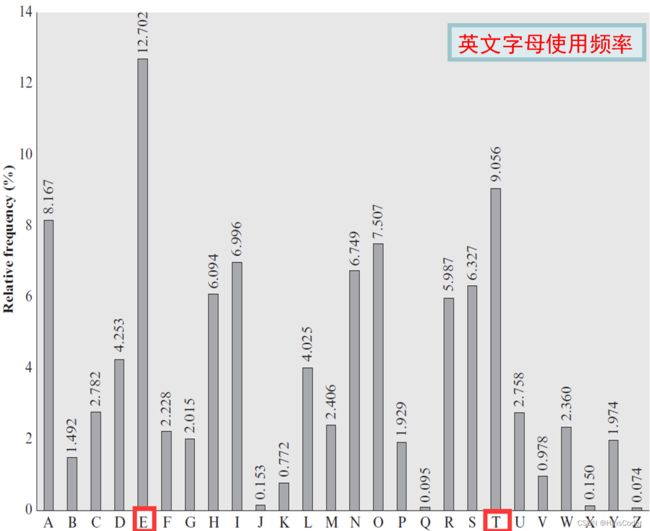
【解决】统计密文的各字母出现频率,将其与现实生活中英文字母使用频率对比
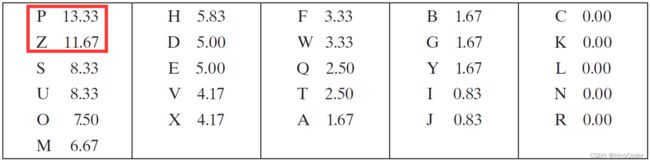
在密文消息中,字母P、Z出现频率最高;它们应该对应现实英文使用频率最高的字母
- 使用频率都是近似值
密文消息的长度有限,我们统计出来的密文字母出现频率都是相对的,只能近似于现实生活的字母使用频率;
先假设密文P对应的就是明文e,密文Z对应的就是明文t,继续推测验证
【解决】统计密文的双字母组合出现频率,将其与现实双字母组合使用频率对比;
上述密文中用的最多的双字母组合是ZW,已知最常用的字母组合是th,所以Z对应t,W对应h;最后一行的ZWP很可能就是the

已知ZWP=the;
对于第一行的ZWSZ,假设它们是一个完整的英文单词,那么对应的明文为th_t,推测它是单词that,即密文S对应的很可能是明文a

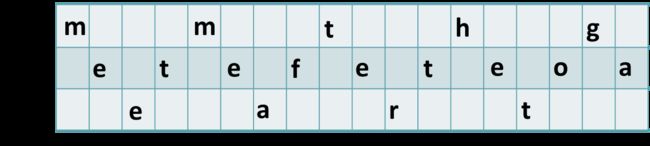
已知ZWPS=thea,将映射分别代入密文中,获得如上所示的不完整明文;
继续进行类似的分析测试,直至推出完整明文。

单表代替密码仍然较容易被攻破,因为它带有原始字母使用频率的一些统计学特征,有两种主要的方法可以减少代替密码里明文结构在密文中的残留度:一种是对明文中的多个字母一起加密,另一种是采用多表代替密码。
3.3 多字母代替密码(Playfair密码)
- Playfair密码是最早的多字母代替密码
- 把明文的双字母代替为密文中的双字母
- 在悬疑小说《Have His Carcase》中也曾提及该密码
- 假设明文为
balloon - 从左到右2个2个地读取,当读取至ll时,该字母对的两个
字母相同,则在它们之间插入任意填充字母如x,继续读取 - 明文变为
ba、lx、lo、on - 如果遇到明文为
奇数对,则在最后补位,如补x - 矩阵中没有字母
J,则明文中的J要被I代换。
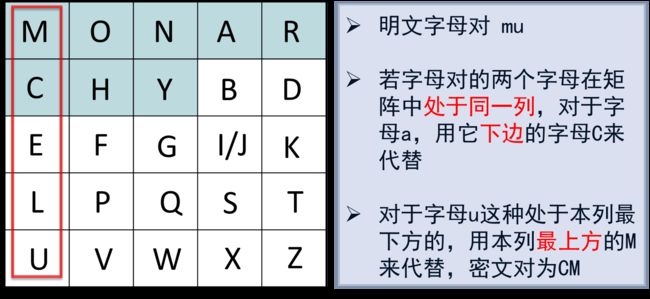
3.3.1 加密
3.3.2 攻击
- 相对安全
Playfair密码尽管只有26个字母,但字母对有26*26=676个,要一一识别比较困难
字母对出现频率远小于单个字母出现频率,统计规律不易发现

尽管Playfair 密码被认为是较安全的,他仍然是相对容易攻破的,因为它的密文仍然完好地保留了明文语言地大部分结构特征。几百个字母地密文就足以我们分析出规律了。
练习题
Alice和Bob选择“MONDAY”作为Playfair加密的密钥词,请画出加密矩阵。并加密明文“jiaoxuelou”
3.4 多表代替加密(Vigenère密码)
Vigenere密码是一种最简单、最著名的多表代替密码
|
|
|
|---|---|
|
|
|
|
3.4.1 加密
3.4.2 解密
3.4.3 攻击
- 若截获的密文中某字母出现频率最高,且近似于字母
E使用频率12.7%,则使用的是单表加密 - 若该密文确定为Vigenere加密,先破解密钥词长度
-
密钥词
deceptive,长度为9,对于某一个密钥序列来说,每隔9位重复一次 -
明文中有两个相同的序列
red,间隔也为9,那么它对应的必然是两个相同的密钥序列 -
明文相同,密钥相同,生成的密文必然也相同
-
若攻击者发现密文中有重复序列“
VTW”,重复的“VTW”间隔为9,则可以推断密钥词长度为9 -
若密文长度足够大,就会有大量的重复序列,计算这些重复序列的间隔公因数,推导密钥长
-
由于密钥词具有周期性,对于密钥字母
d,在第1位、第10位、第19位均出现 -
那么对于明文第1位上的
w、第10位上的o、第19位上的e,它们的加密方式相同,都是+3 -
它们的加密规则一致,即单表加密
-
攻击者也可以猜测密钥长度为
L,那么每隔L位上的密文字母,它们就是单表加密 -
这些字母将具有明文语言的频率特征,也可以一一恢复出对应的明文
3.5 多表代替加密(Vernam密码)
- 既然是密钥词的周期性导致Vigenere密码被攻击,那么选用一个和明文长度相同、并且与明文无任何统计关系的字符串作为密钥
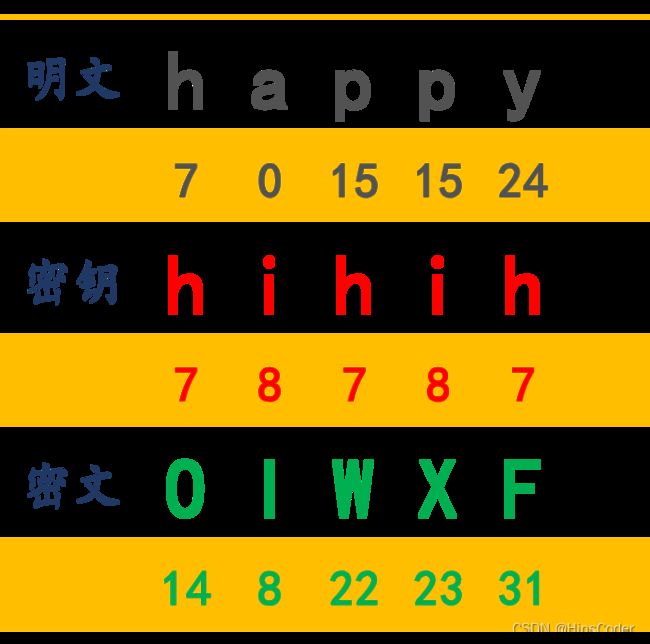
3.5.1 加密
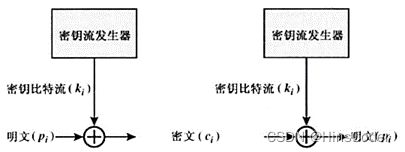
每输入一个明文比特pi,密钥流发生器就产生一个密钥比特ki,二者异或生成密文比特ci
3.5.2 解密
每输入一个密文比特ci,密钥流发生器按加密生成的密钥顺序,读取密钥比特ki,异或还原明文pi
练习题
使用Vernam密码加密信息
“10 110 1110” ,对应的密钥流为 “00 100 1001”,请给出密文。
3.6 一次一密
-
一战时期的陆军情报军官Joseph Mauborgne提出了一种对Vernam密码的改进方案
-
使用与
明文一样长、无重复、随机的密钥来加密消息,该密钥在解密消息后就丢弃不用
- 敌方截获了使用一次一密的密文,还获取了加密过程中的其中2个密钥
- 现在他分别使用这两个密钥进行解密,得到的明文好像都有点语法意义,无法确定我方是用哪个K加密的这条信息
极度安全,很少使用
很难生产出超大规模的真正随机的字符- 双方每发送一条信息就要
依赖一个等长度的密钥来进行加解密,密钥的分配和保护困难。
4. 置换技术
到现在为止我们讨论的都是将明文字母代替位密文字母。与之极不相同的一种加密方法是对明文进行置换,这总密码称为置换密码。
4.1 栅栏技术
- 栅栏技术是一种最简单的基于置换的密码
- 按
对角线的顺序写出明文 - 按
行的顺序读出作为密文,MEMATRHTG ETEFETEOA
- 按
对角线的顺序写出明文 - 按
行的顺序读出作为密文,MMTHG ETEFETEOA EART
4.2 矩阵块
- 给定密钥共7位,将明文按一行7个排成矩阵
- 将明文依次填入矩阵,不足位选
任意字母补齐 - 按
对应列密钥次序读取生成密文
- 为达到更安全的目的,进行第
2次置换 - 将
1次置换生成的密文依次填入矩阵,按列读取
为了更清晰地了解双重置换后的结果,我们用字母所在的位置的序号来代替原始明文信息。于是,共有28个字母的原始消息序列是
5. 多层加密
- 转轮机密码系统是
多层加密最典型的应用
5.1 转轮机
- 二战期间德国的密码系统就是基于一个名为Enigma的转轮机,最后由艾伦·图灵破译,从而扭转盟军在二战中的战局
5.1.1 加密
- 转轮机包含一组相互独立的旋转圆筒;圆筒有
26个输入引脚和26个输出引脚;圆筒内部有连线,将一个输入与一个输出连接 - 把每一个输入和输出当成字母表中的一个字母,那么一个圆筒定义了
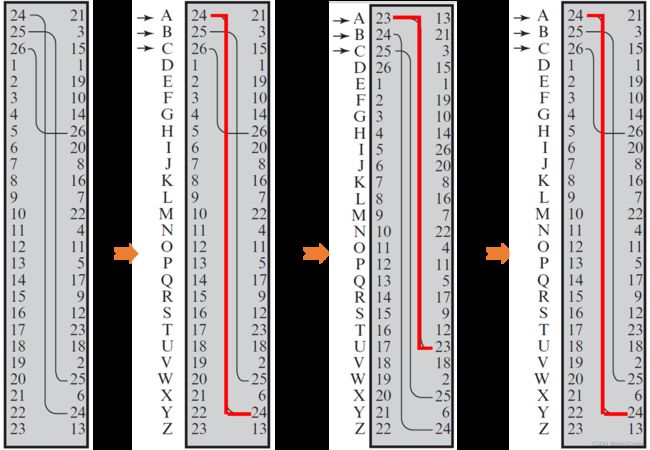
一个单表替换 - 字母a对应的是24号输入引脚,内部连线将其连接在24号输出引脚上,对应的是字母Y;即
明文a对应密文Y - 操作员按下代表字母a的按键。电信号加在了输入引脚上。内部连线将电信号传送到字母Y对应的输出引脚上,转轮机
生成明文a对应的密文Y - 操作员按下输入键并生成一个输出后,圆筒
旋转一个位置 全体输入输出引脚向下移动一位,字母a对应的不再是24号引脚,而变为了23号引脚- 当按下字母a这个输入键时,对应生成的密文为U。即
明文a对应密文U - 当按下了26个字母后,圆筒旋转至最初位置,字母a对应的又是24号引脚,对应的密文又是字母Y了。也就是说一个圆筒包含了26种不同的代替规则。即
一个圆筒包含一个周期为26的多表代替
5.1.2 攻击
-
对于一个明文字母x,流入第一个圆筒,生成密文Y1,有26种可能
-
对于一个密文字母Y1,流入第二个圆筒,生成密文Y2,有26种可能
-
对于一个密文字母Y2,流入第三个圆筒,生成最终密文Y,有26种可能
-
当转轮机包含3个圆筒时,对于一个明文字母X,共有262626种对应的替换方式,即代替规则有17576个
-
五圆筒转轮机相当于一个密钥长度为11881376的Vigenere密码
6. 中英文对照表
OK,以上就是本期知识点“传统加密技术”的知识啦~~ ,感谢友友们的阅读。后续还会继续更新,欢迎持续关注哟~
如果有错误❌,欢迎批评指正呀~让我们一起相互进步
如果觉得收获满满,可以点点赞支持一下哟~