SSA优化章：SSA优化PID

提示：文章写完后，目录可以自动生成，如何生成可参考右边的帮助文档

---

前言

SSA优化PID控制
（博客借鉴了很多大佬的文章和代码，学生仅是以此学习，若有错误请您海涵。）

---

提示：以下是本篇文章正文内容，下面案例可供参考

一、SSA优点

麻雀搜索算法（SSA）是由薛建凯在2020年首次提出，该算法依据麻雀种群的觅食行为和反捕食行为的生物学群体特征提出，通过利用麻雀种群特征和个体特征建立数学模型，在寻找资源过程中，体现了群体搜索的优势，充分模拟了麻雀种群在自然界中的行为模式。相较于其它群体智能优化算法，麻雀搜索算法具有求解精度、效率高等特点。麻雀搜索算法及其优化改进方案目前已应用到了多个工程领域 。

二、使用步骤

---

SSA和传统的优化算法相似， 也是基于种群特征和个体特征建立的数学模型。调用方式和传统的优化算法相同，需要设置好SSA的一些种群数量、迭代次数、参数维度等参数。

fobj = @(X) PID_controller(X,S);%适应度函数
% 之后用上述语句来调用对应的你所需要的优化的适应度函数（fitness）

---

fitness代码如下（示例）：

function [BsJ,r,yout,error]=PID_controller(Kpidi,S)
% PID控制误差--适应度函数
% 输入：Kp、Ki、Kd三个控制参数
% S = 1为单位阶跃响应。S = 2为正弦输入
% 输出： BsJ---控制累计误差
%% 二阶控制系统
ts=0.001;                   % 采样周期
%设一被控对象G（s）=50/(0.125s^2+7s),
sys=tf(50,[0.125,7, 0]); %tf是传递函数  即被控对象函数G（）;  可修改'
dsys=c2d(sys,ts,'z');
[num,den]=tfdata(dsys,'v'); % z变换后的分子分母系数
%%PID控制器
u_1=0.0;u_2=0.0;    % 初始化
y_1=0.0;y_2=0.0;    % 初始化
x=[0,0,0]';         % 初始化
BsJ=0;              % 初始化
error_1=0;          % 初始化
P=1000;              % 控制反馈次数
for k=1:P
    timef(k)=k*ts;
    if(S == 1)
       r(k)=1;        % 控制量1，单位阶跃响应1
    else
       r(k)=0.5*sin(2*pi*k*ts);
    end
    u(k)=Kpidi(1)*x(1)+Kpidi(2)*x(2)+Kpidi(3)*x(3);
    % 控制量越界控制
    if u(k)>=10
        u(k)=10;
    end
    if u(k)<=-10
        u(k)=-10;
    end
    yout(k)=-den(2)*y_1-den(3)*y_2+num(2)*u_1+num(3)*u_2;
    error(k)=r(k)-yout(k);
    % PID控制参数
    u_2=u_1;u_1=u(k);
    y_2=y_1;y_1=yout(k);
    x(1)=error(k);                % P控制量
    x(2)=x(2)+error(k)*ts;        % I控制量 
    x(3)=(error(k)-error_1)/ts;   % D控制量 
    error_1=error(k);   
    
    Ji(k)=0.999*abs(error(k))+0.001*u(k)^2;
    BsJ=BsJ+Ji(k);
    if k>1
        erry(k)=yout(k)-yout(k-1);
        if erry(k)<0
            BsJ=BsJ+100*abs(erry(k));
        end
    end
end
end

---

三.主函数 main.m

代码如下（示例）：

clear all 
clc

SearchAgents_no=50; % Number of search agents 种群数量
Max_iteration=100; % Maximum numbef of iterations 设定最大迭代次数
lb = [-5,2,2]; %下边界
ub = [5,5,5];  %上边界
dim = 3; %维度pid3个参数
S = 1;% 1为单位阶跃响应，其他为正弦输入
fobj = @(X) PID_controller(X,S);%适应度函数
[Best_pos,Best_score,SSA_curve]=SSA(SearchAgents_no,Max_iteration,lb,ub,dim,fobj); %开始优化
figure
plot(SSA_curve,'Color','r','linewidth',2)
hold on
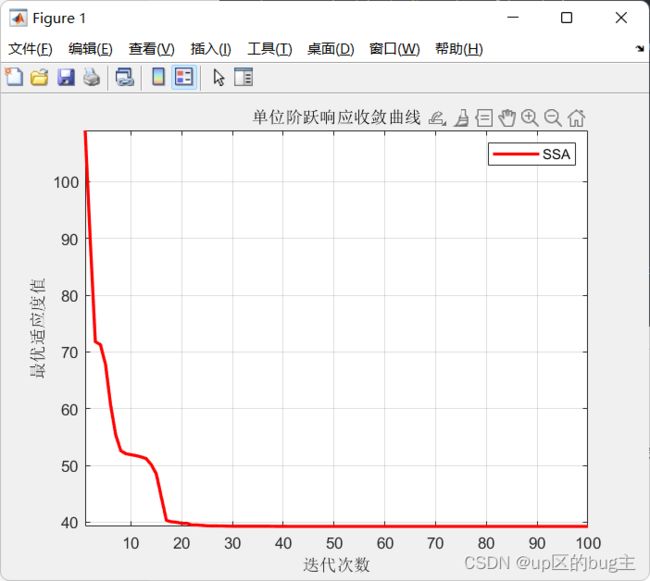
title('单位阶跃响应收敛曲线')
xlabel('迭代次数');
ylabel('最优适应度值');
axis tight
grid on
box on
legend('SSA')
[Bsu,rin,yout,error]=PID_controller(Best_pos,1);S=1时
figure('color',[1,1,1]),
plot(rin,'r--','Linewidth',2);
hold on;
plot(yout,'b-','Linewidth',2)
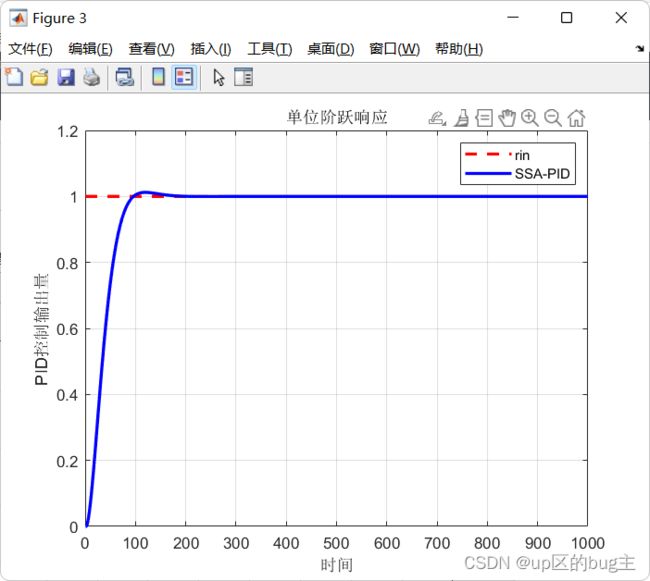
legend('rin','SSA-PID')
xlabel('时间');ylabel('PID控制输出量');
grid on;
title('单位阶跃响应')
disp(['PID值为：',num2str(Best_pos)]);


S = 2;%正弦输入
fobj = @(X) PID_controller(X,S);%适应度函数
[Best_pos,Best_score,SSA_curve]=SSA(SearchAgents_no,Max_iteration,lb,ub,dim,fobj); %开始优化
figure
plot(SSA_curve,'Color','r','linewidth',2)
hold on
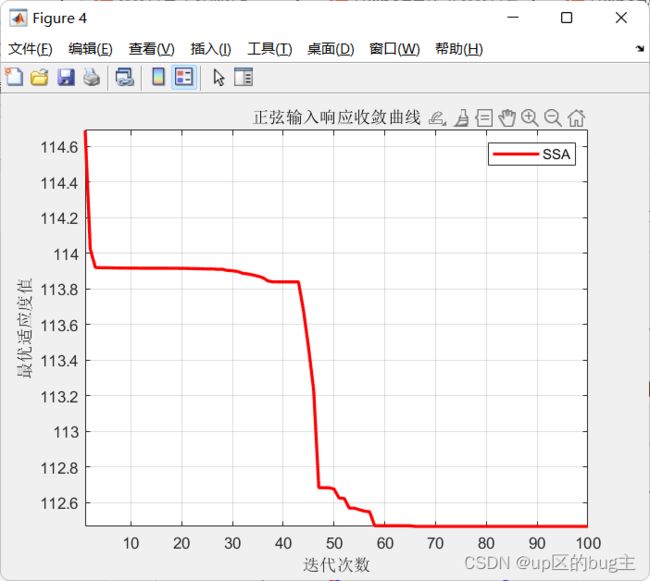
title('正弦输入响应收敛曲线')
xlabel('迭代次数');
ylabel('最优适应度值');
axis tight
grid on
box on
legend('SSA')
[Bsu,rin,yout,error]=PID_controller(Best_pos,S); %S=2 
figure('color',[1,1,1]),
plot(rin,'r--','Linewidth',2);
hold on;
plot(yout,'b-','Linewidth',2)
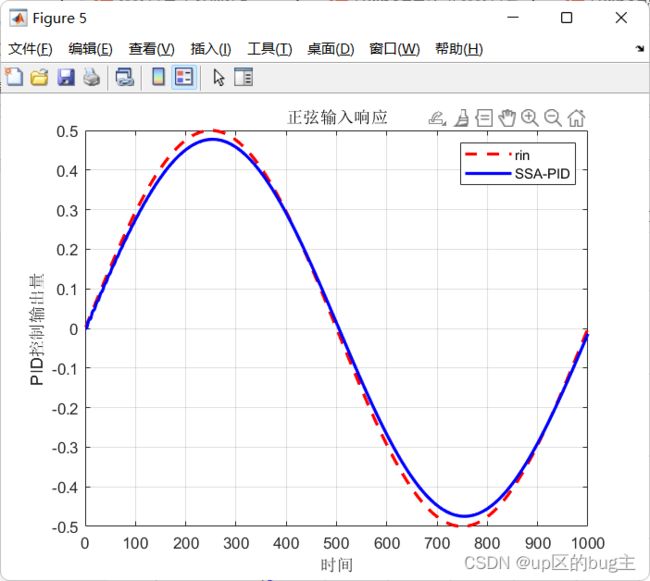
legend('rin','SSA-PID')
xlabel('时间');ylabel('PID控制输出量');
grid on;
title('正弦输入响应')
disp(['PID值为：',num2str(Best_pos)]);

% 麻雀优化算法             %
function [Best_pos,Best_score,curve]=SSA(pop,Max_iter,lb,ub,dim,fobj)

ST = 0.6;%预警值
PD = 0.7;%发现者的比列，剩下的是加入者
SD = 0.2;%意识到有危险麻雀的比重

PDNumber = pop*PD; %发现者数量
SDNumber = pop - pop*PD;%意识到有危险麻雀数量
if(max(size(ub)) == 1)
   ub = ub.*ones(1,dim);
   lb = lb.*ones(1,dim);  
end

%种群初始化
X0=initialization(pop,dim,ub,lb);
X = X0;
%计算初始适应度值
fitness = zeros(1,pop);
for i = 1:pop
   fitness(i) =  fobj(X(i,:));
end
 [fitness, index]= sort(fitness);%排序
BestF = fitness(1);
WorstF = fitness(end);
GBestF = fitness(1);%全局最优适应度值
for i = 1:pop
    X(i,:) = X0(index(i),:);
end
curve=zeros(1,Max_iter);
GBestX = X(1,:);%全局最优位置
X_new = X;
for i = 1: Max_iter
    
    BestF = fitness(1);
    WorstF = fitness(end);
    R2 = rand(1);
   for j = 1:PDNumber
      if(R2<ST)
          X_new(j,:) = X(j,:).*exp(-j/(rand(1)*Max_iter));
      else
          X_new(j,:) = X(j,:) + randn()*ones(1,dim);
      end     
   end
   for j = PDNumber+1:pop
%        if(j>(pop/2))
        if(j>(pop - PDNumber)/2 + PDNumber)
          X_new(j,:)= randn().*exp((X(end,:) - X(j,:))/j^2);
       else
          %产生-1，1的随机数
          A = ones(1,dim);
          for a = 1:dim
            if(rand()>0.5)
                A(a) = -1;
            end
          end 
          AA = A'*inv(A*A');     
          X_new(j,:)= X(1,:) + abs(X(j,:) - X(1,:)).*AA';
       end
   end
   Temp = randperm(pop);
   SDchooseIndex = Temp(1:SDNumber); 
   for j = 1:SDNumber
       if(fitness(SDchooseIndex(j))>BestF)
           X_new(SDchooseIndex(j),:) = X(1,:) + randn().*abs(X(SDchooseIndex(j),:) - X(1,:));
       elseif(fitness(SDchooseIndex(j))== BestF)
           K = 2*rand() -1;
           X_new(SDchooseIndex(j),:) = X(SDchooseIndex(j),:) + K.*(abs( X(SDchooseIndex(j),:) - X(end,:))./(fitness(SDchooseIndex(j)) - fitness(end) + 10^-8));
       end
   end
   %边界控制
   for j = 1:pop
       for a = 1: dim
           if(X_new(j,a)>ub)
               X_new(j,a) =ub(a);
           end
           if(X_new(j,a)<lb)
               X_new(j,a) =lb(a);
           end
       end
   end 
   %更新位置
   for j=1:pop
    fitness_new(j) = fobj(X_new(j,:));
   end
   for j = 1:pop
    if(fitness_new(j) < GBestF)
       GBestF = fitness_new(j);
        GBestX = X_new(j,:);   
    end
   end
   X = X_new;
   fitness = fitness_new;
    %排序更新
   [fitness, index]= sort(fitness);%排序
   BestF = fitness(1);
   WorstF = fitness(end);
   for j = 1:pop
      X(j,:) = X(index(j),:);
   end
   curve(i) = GBestF;
end
Best_pos =GBestX;
Best_score = curve(end);
end

function Positions=initialization(SearchAgents_no,dim,ub,lb)

Boundary_no= size(ub,2); % numnber of boundaries

% If the boundaries of all variables are equal and user enter a signle
% number for both ub and lb
if Boundary_no==1
    Positions=rand(SearchAgents_no,dim).*(ub-lb)+lb;
end

% If each variable has a different lb and ub
if Boundary_no>1
    for i=1:dim
        ub_i=ub(i);
        lb_i=lb(i);
        Positions(:,i)=rand(SearchAgents_no,1).*(ub_i-lb_i)+lb_i;
    end
end

---

四.实验结果

以一个二阶系统传递函数为例：

结合上述的二阶系统传递函数，并利用麻雀搜索算法的寻优性能对其进行优化，以下分别用单位阶跃响应与正弦响应为例，探究麻雀搜索算法优化后的结果。如图2所示为单位阶跃激励下的响应，如图3为其SSA优化迭代过程；如图4所示为正弦激励下的响应，如图5为其SSA优化迭代过程；经过SSA优化后的PID参数值如表2所示。单位阶跃的PID跟踪效果：

正弦输入的PID跟踪效果

SSA迭代曲线对PID控制器的优化效果效果较好，迭代曲线精度随着迭代次数逐渐提升