python高通滤波_python实现直方图均衡化，理想高通滤波与高斯低通滤波

写在前面

HIT大三上学期视听觉信号处理课程中视觉部分的实验二，经过和学长们实验的对比发现每一级实验要求都不一样，因此这里标明了是2019年秋季学期的视觉实验二。

由于时间紧张，代码没有进行任何优化，实验算法仅供参考。

实验要求

实现图像直方图均衡化，要求显示均衡化前、后直方图以及均衡化后图像。

对单通道图像进行DFT变换，要求显示幅度图和相位图，并设计理想高通滤波器和高斯低通滤波器对图像进行频域滤波，并显示滤波之后的图像。 注：除DFT和IDFT外，不允许调库

实验代码

代码首先贴在这里，仅供参考

首先是实现图像直方图均衡化的代码

from ReadBmp import ReadBmp

import matplotlib.pyplot as plt

import numpy as np

filename1 = "1.bmp"

bmp = ReadBmp(filename1)

bmp.gray()

# 统计各像素点数

h = np.array([0 for i in range(256)])

h1 = []

for pixel in bmp.data:

h[pixel[0]] = h[pixel[0]] + 1

h1.append(pixel[0])

# 画出原先的直方图

plt.subplot(1,2,1)

plt.hist(h1, bins = 256)

# 归一化

hs = h / len(bmp.data)

# 计算累计分布

hp = np.array([0.0 for i in range(256)])

for i in range(256):

hp[i] = np.round(np.sum(hs[0:i+1]) * 255)

T = hp.astype('uint8')

# 创建新图像，并统计新图像的各个像素点的个数

hn = np.array([0 for i in range(256)])

h2 = []

for pixel in bmp.data:

s = T[pixel[0]]

pixel[0] = s

pixel[1] = s

pixel[2] = s

hn[pixel[0]] = hn[pixel[0]] + 1

h2.append(s)

bmp.creataBmp("2.bmp")

# 画出新图像的直方图

plt.subplot(1,2,2)

plt.hist(h2, bins = 256)

plt.show()

其中读取bmp图像的程序是我自己写的，这里不再赘述（直接调用了实验一写好的bmp文件读取程序，具体代码见github）

然后是理想高通滤波和高斯低通滤波的程序

import numpy as np

import cv2

import matplotlib.pyplot as plt

def IdealHighPassFiltering(f_shift):

# 设置滤波半径

D0 = 8

# 初始化

m = f_shift.shape[0]

n = f_shift.shape[1]

h1 = np.zeros((m, n))

x0 = np.floor(m/2)

y0 = np.floor(n/2)

for i in range(m):

for j in range(n):

D = np.sqrt((i - x0)**2 + (j - y0)**2)

if D >= D0:

h1[i][j] = 1

result = np.multiply(f_shift, h1)

return result

def GaussLowPassFiltering(f_shift):

# 设置滤波半径

D0 = 8

# 初始化

m = f_shift.shape[0]

n = f_shift.shape[1]

h1 = np.zeros((m, n))

x0 = np.floor(m/2)

y0 = np.floor(n/2)

for i in range(m):

for j in range(n):

D = np.sqrt((i - x0)**2 + (j - y0)**2)

h1[i][j] = np.exp((-1)*D**2/2/(D0**2))

result = np.multiply(f_shift, h1)

return result

img =cv2.imread('1.bmp',0)

f=np.fft.fft2(img)

f_shift=np.fft.fftshift(f)

# 幅度图

s= np.log(abs(f_shift))

# 相位图

p= abs(np.angle(f_shift))

plt.subplot(2,2,1)

plt.imshow(s, 'gray')

plt.subplot(2,2,2)

plt.imshow(p, 'gray')

# 理想高通滤波

IHPF = IdealHighPassFiltering(f_shift)

new_f1 = np.fft.ifftshift(IHPF)

new_image1 = np.uint8(np.abs(np.fft.ifft2(new_f1)))

plt.subplot(2,2,3)

plt.imshow(new_image1, 'gray')

# 高斯低通滤波

GLPF = GaussLowPassFiltering(f_shift)

new_f2 = np.fft.ifftshift(GLPF)

new_image2 = np.uint8(np.abs(np.fft.ifft2(new_f2)))

plt.subplot(2,2,4)

plt.imshow(new_image2, 'gray')

plt.show()

实验结果

实验结果的图像如下图所示

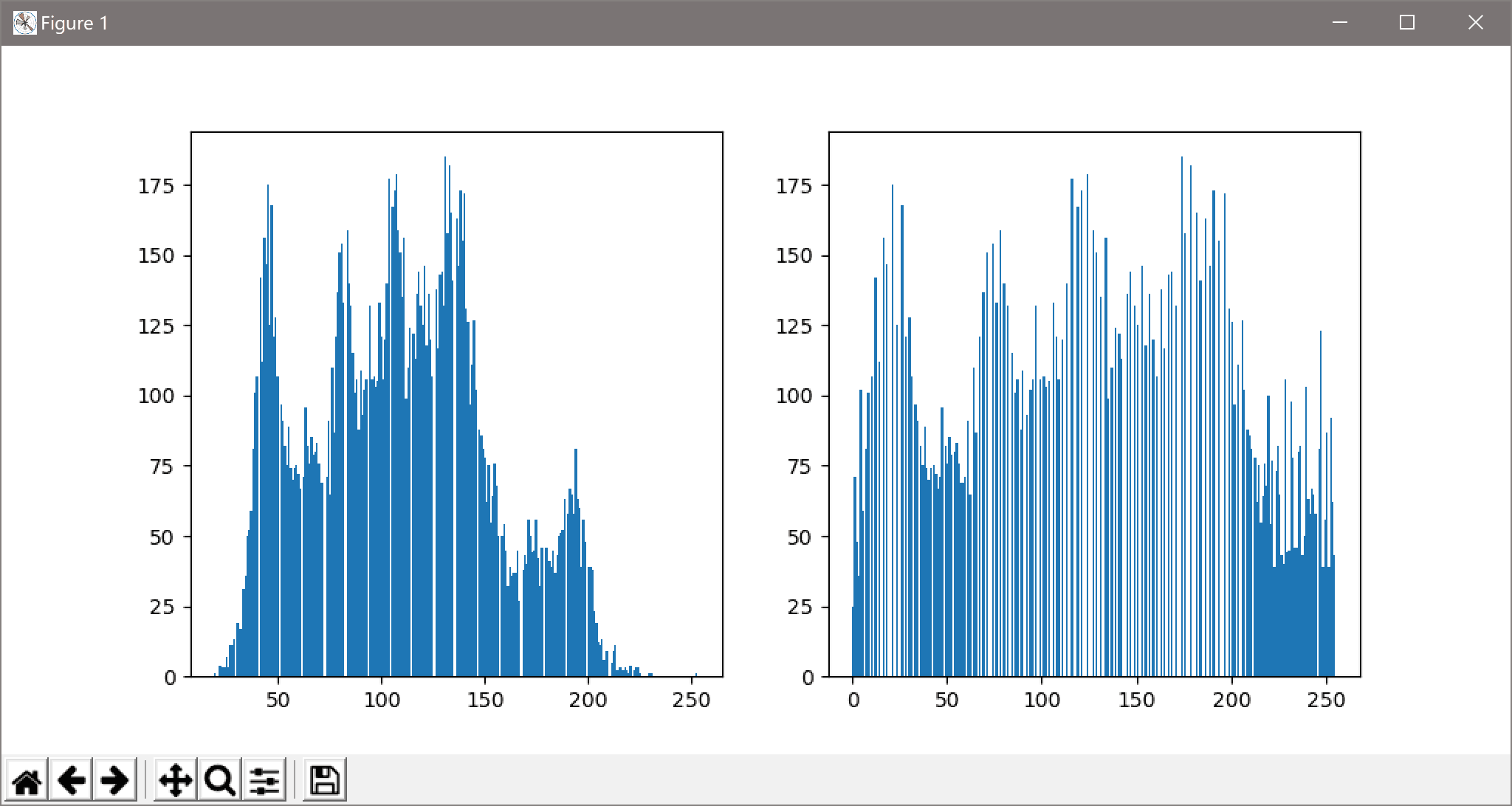
这是直方图均衡化的运行结果，其中左图是做直方图均衡化前对像素统计的直方图，右图是做直方图均衡化后对像素统计的直方图

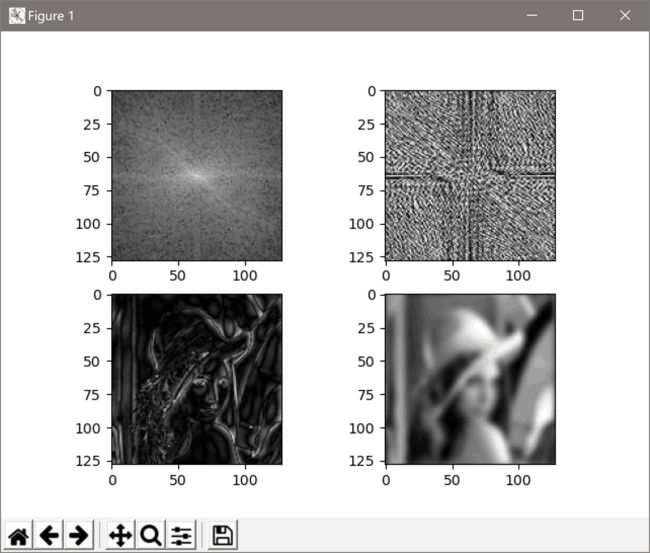
这是画出图像的幅度图和相位图，对图像做理想高通滤波和高斯低通滤波的结果，其中1是幅度图，2是相位图，3是理想高通滤波的结果，4是高斯低通滤波的结果

要点讲解

关于实验算法的大致流程，已在程序中用注释标明，这里只记录需要注意的地方

在直方图均衡化中，要注意直方图函数的用法，该函数可以对输入的矩阵中的数值进行自动的分类，而不用手动分好之后再用直方图函数去画，之前没有仔细看该函数的用法，导致找了好长时间没找到问题。

关于直方图均衡化的原理，需要一定的数学公式的推导，然而其结论十分简单，只有一个公式，对理解公式推导无需求的直接拿公式来用就可以了。（即程序中的归一化加计算累积分布部分）

关于理想高通滤波和高斯低通滤波，可以看到其代码大体框架是一致的，只有中间if语句中的判断条件不一样，理解原理之后直接替换if语句即可。

最终画出理想高通滤波的图像时，网上给出的一些运行结果可能和我们运行的不一致，类似于下图中图一的图像，原因在于这一句话中：new_image1 = np.uint8(np.abs(np.fft.ifft2(new_f1)))，注意到中间调用了np.abs()函数，由于经过DFT变换之后所得的数值是复数，而不是实数，若将np.abs()替换为np.real()，即只取其实部，则得到的是图一，而使用np.abs()，得到的则是图二。个人感觉图二才是相对正确一些的结果，图一相当于将虚部舍弃掉了，这是不太好的。

以下是图一

以下是图二

知识总结

关于直方图均衡化的数学原理，我参考的是这篇博客。直方图均衡化的公式推导较为复杂，然而其结果却十分简单，因此在python中一个循环就实现了。

直方图均衡化的数学原理

其中在理想高通和高斯低通滤波器中，需要用到矩阵乘法，关于几种不同的矩阵乘法参考的是这篇博客

numpy 三种矩阵乘法

实验总结

很简单的一个实验，总时间加起来大致4个小时左右，做这么快的主要原因是，本来同学来哈尔滨找我玩，正玩得开心，结果突然告诉我这个实验要今天晚上交（之前以为这个实验还有一周的ddl），所以潜能爆发，从三点写到六点差不多就写完了