上海交大ACM班C++算法与数据结构——C++算法初级1
上海交大ACM班C++算法与数据结构——C++算法初级1
1.算法
- 目标:用一个算法解决一类问题
- 不仅要符合数学规律,还要有实际意义
- 算法描述方法:
- 自然语言:方便面对面交流
- 流程图:直观
- 伪代码:可以清晰了解程序流程,并便于计算出复杂度,忽略一些代码实现的细节
- 程序语言:与计算机沟通算法
- 特性:
- 有穷性:算法的指令或者步骤的执行次数和时间都是有限的;
- 确切性:算法的指令或步骤都有明确的定义,无二义性;
- 可行性:算法的执行步骤必须是可行的。
- 输入、输出
2.数据结构
- 研究数据的存储方式(考虑数据的逻辑结构和物理结构),及在特定存储方式下的处理方法
- 常见操作:创建与清除、插入与删除、检索与访问与更新、遍历、排序
3.模拟算法
- 用脚本(如:bash脚本)调用不同代码完成一系列工作来模拟人手动运行不同代码
- 不是一种算法,是一种以编程基本功为主的实现方法,将一系列操作串联起来,固定实现一个一直流程(对一种已知的固定流程的模拟)
- 要求我们对数组、字符串等操作非常熟悉,才能找到更优美的实现方法
4.高精度运算
-
所有相关大整数的操作本质就是模拟,模拟人工处理大整数的过程
-
单精度:能用一个内置类型存储的整数,unsigned long long数据类型能存储的最大数为2的64次幂-1
双精度:不能用内置类型存储的大整数,通常用数组存储每一个数位 -
为了方便模拟竖式计算,采用小端序(与书写顺序相反,低位在前,存储在地址的低位)存储双精度大整数 ,如2021的小端序存储:
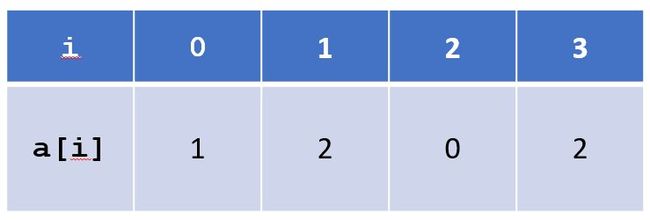
加减法都是从地位开始运算,小端序地位处于地址的地位,循环枚举的时候符合正向枚举的习惯,而且位数的变化更加方便,容易实现数组伸缩。 -
乘法:一个n位的整数和一个m位的整数相乘,结果最多为n + m位的整数,最少为1位
-
练习题目1:
- 高精度减法:
输入两个大整数ab,计算a - b的结果,其中数据保证0 < b < a < 10^500。
输入描述:一行,两个大整数ab,中间用空格隔开。
输出描述:一行一个整数,表示a-b的结果。
示例 1:
输入:10000 9990
输出:10
代码:
- 高精度减法:
#include -
练习题目2:
- 高精度乘法:
求两数的积。说明/提示:每个数字不超过 10^2000 ,需用高精度。
输入描述:两行,两个整数。
输出描述:一行一个整数表示乘积。
示例 1:
输入:
123456789
987654321
输出:
121932631112635269
#include
ans_digits[i+j]=a_digits[i]*b_digits[j]+ans_digits[i+j] ;}
//cout<
// ans的每一位更新都要使用累加的形式,这是因为对于ans的第k位,满足i + j == k的(i, j)很多,所以可能答案的第k位可能先后被更新很多次。
// 2. 统一进位
int k = 0;
for (int i = 0; i < ans_len; ++i) {
// TODO 请补全下述代码
ans_digits[i]+=k;
k=ans_digits[i]/10;
ans_digits[i]%=10;
//cout<
}
// 3. 维护长度
while (ans_len > 1 && ans_digits[ans_len - 1] == 0)
--ans_len;
// 4. 输出
for (int i = ans_len - 1; i >= 0; --i)
cout << ans_digits[i];
cout << endl;
return 0;
}
-
练习题目3:
- 高精度加法:
高精度加法,相当于a+b problem,不用考虑负数.
输入描述:分两行输入。a, b ≤ 10^10000
输出描述:输出只有一行,代表a+b的值
示例 1:
输入:
1001 9099
输出:
10100
#include 5.算法复杂度
-
时间复杂度
- 主频:CPU每秒钟产生脉冲信号的次数(也就是每秒钟的时钟周期个数)
以2.1GHz为例,一秒钟该CPU可以产生2.1*10^9次脉冲信号,如果一台计算机每个时钟周期可以完成1条指令,那么该计算机1s之内就可以运行2.1 *10^9条指令。 - 时钟周期:计算机计量时间的最小单位
例:在一台主频为2.1GHz的电脑上,如果一台计算机每个时钟周期可以完成1条指令,如果一个算法需要10{20}条指令,那么它的运行时间将是10{20}(2*109)\3600\24÷(2∗109)÷3600÷24,答案约等于 580000
- 主频:CPU每秒钟产生脉冲信号的次数(也就是每秒钟的时钟周期个数)
-
空间复杂度
一个5000 * 5000的二维数组int a所耗内存为5000×5000×4÷1024÷1024≈95 MB。(一个int占4个字节,1M=1024K,1K=1024bite)
还要考虑具体实现难度和一些针对实际问题的评价指标 -
提高算法时间复杂度的指导思想:充分利用每一次计算结果(对计算机的劳动成果报以最大尊重),但同时会因为对中间计算结构的存储(以方便再次利用),会加大空间复杂度。
-
空间复杂度和时间复杂度通常会此消彼长,牺牲一个来成全另一个
6.暴力枚举
-
利用计算机运算速度快、精确度高的特点,对要解决问题的所有可能情况,一个不漏地进行检验,从中找出符合要求的答案的方法
-
子集枚举:
- 比特串法:集合{1,2,3,4,5,6},000101表示子集{4,6}(0表示对应元素不包含在子集中,1则表示包含在子集中)假设我们有个集合{1,2,3,…,n},输出所有满足集合中所有数求和是3的倍数的子集的个数。
#include - 数组表示法递归枚举:可以根据实际情况进行剪枝,复杂度优于二进制串法
7.排列枚举:
-
一种用一维数组表达二维信息的方式:把列看成数组的下标,行看成数组里的值的话,如下图所示

对应数组:int a[10] = {0, 5, 7, 1, 4, 2, 8, 6, 3}; // 这里我们从1开始存储,0号无意义。 -
STL(Standard Template Library):标准模板库,分为算法(algorithm)、容器(container)和迭代器(iterator)三个部分,之所以叫做“模板库”,是因为在STL中几乎所有代码都是用模板类或者模板函数的方式实现的。
-
next_permutation:3个参数,分别代表头指针(重拍范围包含头指针所指元素),尾指针(重拍范围不包含尾指针所指元素)和比较函数(可选)。
会将数组重拍成更大的数组,并返回Ture或False,False代表传入数组已经是最大的了,但是仍然会把数组改变从最小的,如:
int a[10] = {4, 3, 2, 1};
if (next_permutation(a, a + 4)) {
cout << "Yes" << endl;
} else {
cout << "No" << endl;
}
for (int i = 0; i < 4; ++i) cout << a[i] << ' ';
cout << endl;
输出结果:
No
1 2 3 4
可以利用这种办法重拍数组下标实现一维数组元素所有排列的遍历。
调用next_permutation函数一次的复杂度为O(n)。如果对于不同元素的排列,如果连续调用next_permutation函数的话,均摊复杂度为O(1)。

