LMS自适应滤波的MATLAB实现——实例仿真
在此之前我写过了“LMS自适应滤波的MATLAB实现”方法,仅仅强调实现方式,并没有举例仿真,所以本章内容主要对之前两种实现方法进行实例仿真,以说明方法的有效性。
LMS实现方法的博客:
https://blog.csdn.net/weixin_44386642/article/details/124104911
1、自己编写的子函数
这个子函数是在别人的基础上进行改进的,效果较好,命名为“LMS_dps”,调用格式:
[yn,W,en,u] = LMS_dps(xn,dn,M,mu,itr)%itr:迭代次数可以不设置
注意:由于实际语音信号接收到的噪声比较复杂,因此这里主要讨论由多个频率的正弦信号叠加产生的混合噪声。单个频率的加性噪声滤波方法可以采用传统的固定式滤波,即IIR和FIR滤波器,或者用自适应带陷滤波;可以参见我的另一篇博客。
https://blog.csdn.net/weixin_44386642/article/details/124354352
实例:原信号和带噪信号都采用正弦函数生成。语音信号f=300HZ,噪声信号为多频正弦信号的叠加,f1=50HZ,f2=500HZ,f3=1000HZ。代码如下:
clc;clear;close all;
%% LMS自适应滤波
%参数:语音信号f=300HZ,噪声信号为多频正弦信号的叠加,f1=50HZ,f2=500HZ,f3=1000HZ
fs=8000;%采样频率
F=300;
F1=50;
F2=500;
F3=1000;
t=(0:1:999)/fs;
y=sin(2*pi*F*t);%语音信号
noise=sin(2*pi*F3*t);%噪声3
noise1=sin(2*pi*F1*t);%噪声1
noise2=sin(2*pi*F2*t);%噪声2
Noise=noise+noise1+noise2;
Y=y+Noise;%带噪信号
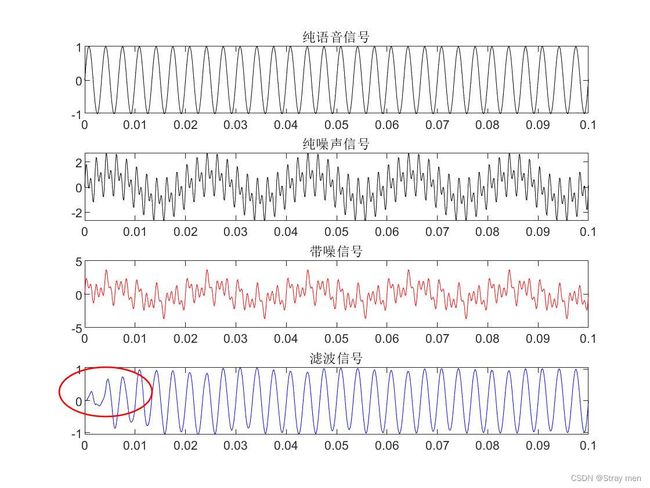
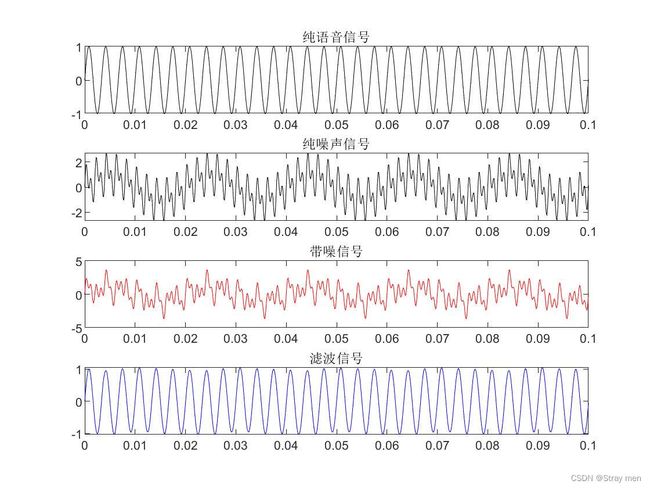
figure(1),subplot 411;plot(t,y,'k');xlim([0 0.1]);title('纯语音信号');
subplot 412;plot(t,Noise,'k');xlim([0 0.1]);title('纯噪声信号');
subplot 413;plot(t,Y,'r');xlim([0 0.1]);title('带噪信号');
l = 32;%设定FIR滤波器参数,设定一个长度为32的FIR滤波器
mu1=rand()*0.0054;%收敛因子(小于最大收敛因子u)
lms = dsp.LMSFilter('Length',l,'StepSize',mu1);%设置lms长度L为32,步长为0.008
[z,err,wts]=lms(Y',y');
M=32;%滤波器阶数
mu=rand()*0.0054;%收敛因子(小于最大收敛因子u)
fprintf('实际取值收敛因子mu=%5.4f \n',mu);
[yn,W,en,u] = LMS_dps(Y',y',M,mu);
% figure(1),subplot 414;plot(t,z,'b');xlim([0 0.1]);title('滤波信号');
figure(1),subplot 414;plot(t,yn,'b');xlim([0 0.1]);title('滤波信号');
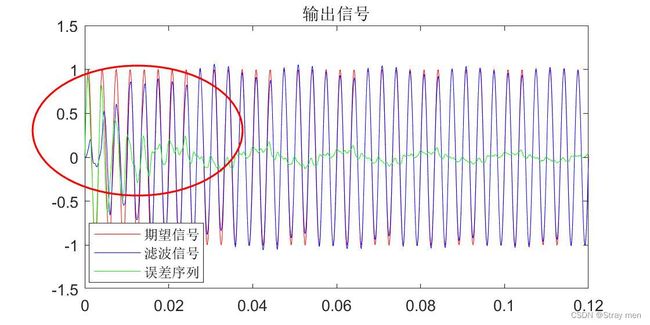
figure(2),plot(t,y,'r',t,yn,'b',t,en,'g');legend('期望信号','滤波信号','误差序列');xlim([0 0.15]);
% %---------探究收敛因子对滤波性能的影响
% %结论:在小于最大收敛因子范围内,随着收敛因子的增加,滤波性能得到提升;
% %-----当超过之后,滤波性能会随着下降。
% mu=linspace(0.0001,0.01,10);
% M=32;
% for i=1:length(mu)
% mu_1=mu(i);
% fprintf('实际取值收敛因子mu=%5.4f \n',mu_1);
% [yn,W,en,u] = LMS_dps(Y',y',M,mu_1);
% snr=SNR_singlech(y,yn);
% fprintf('信噪比SNR=%5.4f \n',snr);
% plot(t,en);hold on
% end
注意:函数“LMS_dps”在最开始引用的博客里面。结果如下:
滤波输出序列的结果:

总结:可以发现滤波的效果较好,误差很小。
2、直接调用MATLAB自带的LMS自适应滤波函数
注意:由自带函数进行自适应滤波输出的结果具有延迟效应,这是因为滤波过程中调用了FIR滤波器产生了延迟效应。要改善延迟可以适当增大步长,但是不能超过最大范围;因为超出后滤波效果会降低。而函数"LMS_dps"没有延迟,是因为调整了输出区间,可在函数中查看。
总结
总体而言,调用函数"LMS_dps"的滤波效果最好,在实际处理真实语音信号过程中,滤波后的信噪比也要大于自带的滤波输出,且没有延迟。但是自带的滤波过程快速,实现简单,对于前导无话帧噪声较小的语音信号或者信噪比不是很低的语音信号还是具有较强的适用性。