【西瓜书笔记】5. 软间隔与支持向量机回归
5.1 软间隔SVM
之前我们使用的是严格线性可分的硬间隔SVM:
min w , b 1 2 ∥ w ∥ 2 s.t. 1 − y i ( w T x i + b ) ⩽ 0 , i = 1 , 2 , … , m \begin{array}{ll} \min _{\boldsymbol{w}, b} & \frac{1}{2}\|\boldsymbol{w}\|^{2} \\ \text { s.t. } & 1-y_{i}\left(\boldsymbol{w}^{\mathrm{T}} \boldsymbol{x}_{i}+b\right) \leqslant 0, \quad i=1,2, \ldots, m \end{array} minw,b s.t. 21∥w∥21−yi(wTxi+b)⩽0,i=1,2,…,m
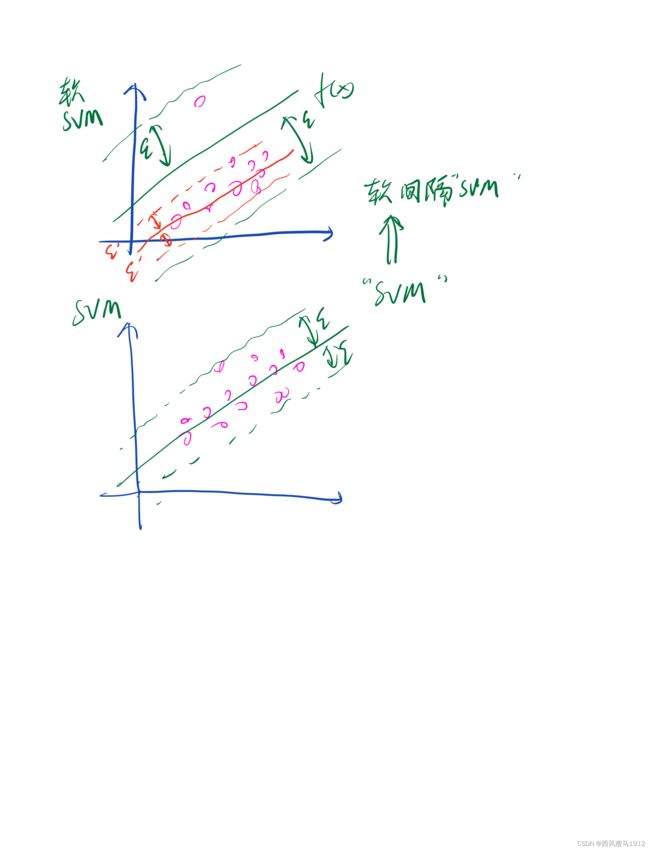
然而实际场景中,可能面对如下图所示的两种问题:
- 严格线性可分的数据并不总是存在。
- 有可能产生过拟合
那么就需要适当放松约束条件。软间隔SVM允许某些样本不满足函数间隔值大于等于1这个约束,也即允许函数间隔值小于1.当然,这样的样本尽量越少越好。因此优化问题可以改写为线性不可分时的软间隔SVM
min w , b 1 2 ∥ w ∥ 2 + C ∑ i = 1 m ℓ 0 / 1 ( y i ( w T x i + b ) − 1 ) \min _{w, b} \quad \frac{1}{2}\|\boldsymbol{w}\|^{2}+C \sum_{i=1}^{m} \ell_{0 / 1}\left(y_{i}\left(\boldsymbol{w}^{\mathrm{T}} \boldsymbol{x}_{i}+b\right)-1\right) w,bmin21∥w∥2+Ci=1∑mℓ0/1(yi(wTxi+b)−1)
其中
l 0 / 1 ( z ) = { 0 , if z ≥ 0 1 , otherwise l_{0 / 1}(z)=\left\{\begin{array}{l} 0, \text { if } z \geq 0 \\ 1, \text { otherwise } \end{array}\right. l0/1(z)={0, if z≥01, otherwise
但是将0-1函数代回到目标函数进行优化时,会产生麻烦,因为0-1函数它不是个凸函数,且不连续。
由于 l 0 / 1 ( z ) l_{0/1}(z) l0/1(z)非凸、不连续,数学性质不太好(导数为0),不易优化求解,因此需要考虑用其他损失函数来近似替代 l 0 / 1 ( z ) l_{0/1}(z) l0/1(z),软间隔SVM选的替代损失函数是合页(hinge)损失函数
ℓ hinge ( z ) = max ( 0 , 1 − z ) \ell_{\text {hinge }}(z)=\max (0,1-z) ℓhinge (z)=max(0,1−z)
合页损失可以理解为:待考察变量 z z z如果大于等于1就不惩罚,但是如果小于1就需要惩罚,但是惩罚的程度取决于自身比1小的程度,显然合页损失很适合用来考察软间隔 SVM里面的函数间隔值。
将优化问题中的 ℓ 0 / 1 \ell_{0/1} ℓ0/1损失函数更换为合页函数可得:
min w , b 1 2 ∥ w ∥ 2 + C ∑ i = 1 m max ( 0 , 1 − y i ( w T x i + b ) ) \min _{\boldsymbol{w}, b} \quad \frac{1}{2}\|\boldsymbol{w}\|^{2}+C \sum_{i=1}^{m} \max \left(0,1-y_{i}\left(\boldsymbol{w}^{\mathrm{T}} \boldsymbol{x}_{i}+b\right)\right) w,bmin21∥w∥2+Ci=1∑mmax(0,1−yi(wTxi+b))
为了引入松弛因子,令
max ( 0 , 1 − y i ( w T x i + b ) ) = ξ i \max \left(0, 1-y_{i}\left(\boldsymbol{w}^{\mathrm{T}} \boldsymbol{x}_{i}+b\right)\right)=\xi_{i} max(0,1−yi(wTxi+b))=ξi
则上述优化问题可以改写为:
min w , b , ξ i 1 2 ∥ w ∥ 2 + C ∑ i = 1 m ξ i s.t. y i ( w T x i + b ) ⩾ 1 − ξ i ξ i ⩾ 0 , i = 1 , 2 , … , m \begin{gathered} \min _{\boldsymbol{w}, b, \xi_{i}} \quad \frac{1}{2}\|\boldsymbol{w}\|^{2}+C \sum_{i=1}^{m} \xi_{i} \\ \text { s.t. } y_{i}\left(\boldsymbol{w}^{\mathrm{T}} \boldsymbol{x}_{i}+b\right) \geqslant 1-\xi_{i} \\ \xi_{i} \geqslant 0, i=1,2, \ldots, m \end{gathered} w,b,ξimin21∥w∥2+Ci=1∑mξi s.t. yi(wTxi+b)⩾1−ξiξi⩾0,i=1,2,…,m
C是超参数权重。这里注意,如果 1 − y i ( w T x i + b ) ≤ 0 1-y_{i}\left(\boldsymbol{w}^{\mathrm{T}}\boldsymbol{x}_{i}+b\right)\leq0 1−yi(wTxi+b)≤0,那么 1 − y i ( w T x i + b ) ≤ ξ i = 0 1-y_{i}\left(\boldsymbol{w}^{\mathrm{T}}\boldsymbol{x}_{i}+b\right)\leq\xi_{i}=0 1−yi(wTxi+b)≤ξi=0。如果 1 − y i ( w T x i + b ) > 0 1-y_{i}\left(\boldsymbol{w}^{\mathrm{T}}\boldsymbol{x}_{i}+b\right)>0 1−yi(wTxi+b)>0, 那么 1 − y i ( w T x i + b ) = ξ i 1-y_{i}\left(\boldsymbol{w}^{\mathrm{T}}\boldsymbol{x}_{i}+b\right)=\xi_{i} 1−yi(wTxi+b)=ξi 。所以 y i ( w T x i + b ) ⩾ 1 − ξ i y_{i}\left(\boldsymbol{w}^{\mathrm{T}} \boldsymbol{x}_{i}+b\right) \geqslant 1-\xi_{i} yi(wTxi+b)⩾1−ξi.
这时,优化问题与原始SVM优化问题相比,只是多了一个变量 ξ \xi ξ,所以优化步骤和方法与之前一样。
支持向量回归
SVR和SVM唯一的联系就是优化目标函数很相像,但是其建模思路差别很大。SVR实际就 是找一个以 f ( x ) f(x) f(x)为中心,宽度为 2 ϵ 2\epsilon 2ϵ的间隔带,使得此间隔带尽可能多地把所有样本都包裹住。
由外向内的思路:假设这条间隔带能包裹住所有样本,那么有两种方式可以做到,一种是 ϵ \epsilon ϵ取任意大,那么以任意 f ( x ) f(x) f(x)为中心的间隔带都能把所有样本包裹住,但是显然这样是没有意义的。另一种就是找尽可能小的 ϵ \epsilon ϵ使得其能把所有样本包裹住,那么能把所有样本包裹住的间隔带的 ϵ \epsilon ϵ最小是多少呢?可以通过以下优化问题来求解
min w , b , ϵ ϵ s.t. − ϵ ⩽ y i − f ( x i ) ⩽ ϵ \begin{array}{cl} \min_{\boldsymbol{w}, b, \epsilon} & \epsilon \\ \text { s.t. } & -\epsilon \leqslant y_{i}-f\left(\boldsymbol{x}_{i}\right) \leqslant \epsilon \end{array} minw,b,ϵ s.t. ϵ−ϵ⩽yi−f(xi)⩽ϵ
这里 f ( x ) = w T x i + b f(x)=\boldsymbol{w}^{\mathrm{T}} \boldsymbol{x}_{i}+b f(x)=wTxi+b.
但是由于实际采样得到的样本会存在极个别偏离大多数样本很远的噪音,那么此时如果按照以上优化目标来进行求解的话也会导致 ϵ \epsilon ϵ偏大。如下图所示
因此,通常都会考虑人为固定 ϵ \epsilon ϵ的取值。 显然,一旦固定 ϵ \epsilon ϵ后上述优化问题就会无法求解,因此需要给固定后的 ϵ \epsilon ϵ两边添加未知因素松弛因子,同时也希望松弛因子不要太大
min w , b , ξ , ξ ^ ϵ + ∑ i = 1 m ( ξ i + ξ ^ i ) s.t. − ϵ − ξ i ⩽ y i − f ( x i ) ⩽ ϵ + ξ ^ i ξ i ≥ 0 ξ ^ i ≥ 0 \begin{array}{cl} \min _{\boldsymbol{w}, b,\xi, \hat{\xi} } & \epsilon+\sum_{i=1}^{m}\left(\xi_{i}+\hat{\xi}_{i}\right) \\ \text { s.t. } & -\epsilon-\xi_{i} \leqslant y_{i}-f\left(\boldsymbol{x}_{i}\right) \leqslant \epsilon+\hat{\xi}_{i} \\ & \xi_{i} \geq 0 \\ & \hat{\xi}_{i} \geq 0 \end{array} minw,b,ξ,ξ^ s.t. ϵ+∑i=1m(ξi+ξ^i)−ϵ−ξi⩽yi−f(xi)⩽ϵ+ξ^iξi≥0ξ^i≥0
这里注意,
- f ( x ) f(\boldsymbol{x}) f(x)左右两边的松弛因子不一样
- 而且这里 ( ξ , ξ ^ ) (\xi,\hat{\xi}) (ξ,ξ^)是一对一对出现的,所以总共有2m个松弛因子
而且因为我们已经固定了 ϵ \epsilon ϵ,可以简化为
min w , b , ξ , ξ ^ ∑ i = 1 m ( ξ i + ξ ^ i ) s.t. − ϵ − ξ i ⩽ y i − f ( x i ) ⩽ ϵ + ξ ^ i ξ i ≥ 0 ξ ^ i ≥ 0 \begin{array}{cl} \min _{\boldsymbol{w}, b,\xi, \hat{\xi} } & \sum_{i=1}^{m}\left(\xi_{i}+\hat{\xi}_{i}\right) \\ \text { s.t. } & -\epsilon-\xi_{i} \leqslant y_{i}-f\left(\boldsymbol{x}_{i}\right) \leqslant \epsilon+\hat{\xi}_{i} \\ & \xi_{i} \geq 0 \\ & \hat{\xi}_{i} \geq 0 \end{array} minw,b,ξ,ξ^ s.t. ∑i=1m(ξi+ξ^i)−ϵ−ξi⩽yi−f(xi)⩽ϵ+ξ^iξi≥0ξ^i≥0
为了和SVM的优化问题保持形式一致,从而方便继承SVM自带的一套东西,可以考虑加一 个L2正则项,也即
min w , b , ξ , ξ ^ 1 2 ∥ w ∥ 2 + ∑ i = 1 m ( ξ i + ξ ^ i ) s.t. − ϵ − ξ i ⩽ y i − f ( x i ) ⩽ ϵ + ξ ^ i ξ i ≥ 0 ξ ^ i ≥ 0 \begin{array}{cl} \min _{\boldsymbol{w}, b,\xi, \hat{\xi} } & \frac{1}{2}\|w\|^{2}+\sum_{i=1}^{m}\left(\xi_{i}+\hat{\xi}_{i}\right) \\ \text { s.t. } & -\epsilon-\xi_{i} \leqslant y_{i}-f\left(\boldsymbol{x}_{i}\right) \leqslant \epsilon+\hat{\xi}_{i} \\ & \xi_{i} \geq 0 \\ & \hat{\xi}_{i} \geq 0 \end{array} minw,b,ξ,ξ^ s.t. 21∥w∥2+∑i=1m(ξi+ξ^i)−ϵ−ξi⩽yi−f(xi)⩽ϵ+ξ^iξi≥0ξ^i≥0
通常还会考虑给松弛因子添加一个正则化常数C(C越大,优化就更关注松弛因子项),同时约束条件也可以进行恒等变形,进 而也就得到了常见的SVR优化问题
min w , b , ξ , ξ ^ 1 2 ∥ w ∥ 2 + C ∑ i = 1 m ( ξ i + ξ ^ i ) s.t. − ϵ − ξ i ⩽ y i − f ( x i ) ⩽ ϵ + ξ ^ i ξ i ≥ 0 ξ ^ i ≥ 0 \begin{array}{cl} \min _{\boldsymbol{w}, b,\xi, \hat{\xi} } & \frac{1}{2}\|w\|^{2}+C\sum_{i=1}^{m}\left(\xi_{i}+\hat{\xi}_{i}\right) \\ \text { s.t. } & -\epsilon-\xi_{i} \leqslant y_{i}-f\left(\boldsymbol{x}_{i}\right) \leqslant \epsilon+\hat{\xi}_{i} \\ & \xi_{i} \geq 0 \\ & \hat{\xi}_{i} \geq 0 \end{array} minw,b,ξ,ξ^ s.t. 21∥w∥2+C∑i=1m(ξi+ξ^i)−ϵ−ξi⩽yi−f(xi)⩽ϵ+ξ^iξi≥0ξ^i≥0
这就是西瓜书上的式6.45。就可以进一步套用支持向量机的优化过程了。