读论文系列【一】：VAE/GAN网络结构的介绍

摘要

  自动编码器(AE)是数据检索，数据降噪的有力工具，变分自动编码器(VAE)更是一种有效的生成模型。14年生成对抗网络（GAN）的提出，为图像处理，信号处理等领域提供了新的处理工具。我以VAE/GAN这一篇经典的网络结构为主，辅以GAN和VAE的概念，对这一篇论文进行了分析和总结。
  论文：Anders Boesen, Lindbo Larsen, Søren Kaae Sønderby, Hugo Larochelle, Ole Winther“Autoencoding beyond pixels using a learned similarity metric” , ICML. 2016

Variational Autoencoder

  VAE作为一种生成模型，在生成能力方面和GAN有着不同的优点和缺陷。
为方便理解分析，参考一位博主的blog，引入如下的图片例子。

  普通的卷积神经网络的输入向量为one-hot向量，很稀疏。为了解决这个问题，我们想使用实数值向量而不是0，1向量。我们可认为这种实数值向量是原图片的一种编码，这也就引出了编码/解码的概念。举个例子，[3.3, 4.5, 2.1, 9.8]代表猫，[3.4, 2.1, 6.7, 4.2] 代表狗。这个已知的初始向量可以作为我们的潜在变量。

AE

  如果像我上面一样，随机初始化一些向量去代表图片的编码，这不是一个很好的办法，我们更希望计算机能帮我们自动编码。在autoencoder模型中，我们加入一个编码器，它能帮我们把图片编码成向量。然后解码器能够把这些向量恢复成图片。

  AE的主要用途用于降维分析，初始化神经网络，数据降噪以及数据检索（文本，图片）等方面。

VAE

  我们可以对编码器添加约束，就是强迫它产生服从单位高斯分布的潜在变量。正是这种约束，把VAE和标准自编码器给区分开来了。现在，产生新的图片也变得容易：我们只要从单位高斯分布中进行采样，然后把它传给解码器就可以了。
  对于我们的损失函数，我们可以把这两方面进行加和。一方面，是图片的重构误差，我们可以用平均平方误差来度量，另一方面。我们可以用KL散度来度量我们潜在变量的分布和单位高斯分布的差异。算法见下图，图自原论文。

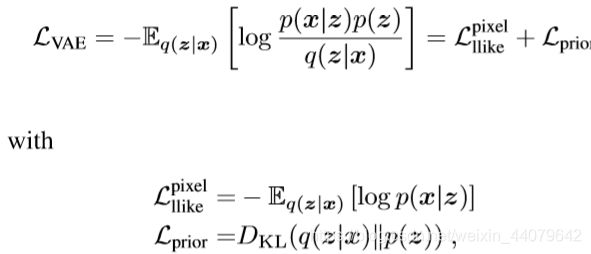
VAE的Loss
  为了优化KL散度，我们需要应用一个简单的参数重构技巧：不像标准自编码器那样产生实数值向量，VAE的编码器会产生两个向量:一个是均值向量，一个是标准差向量。

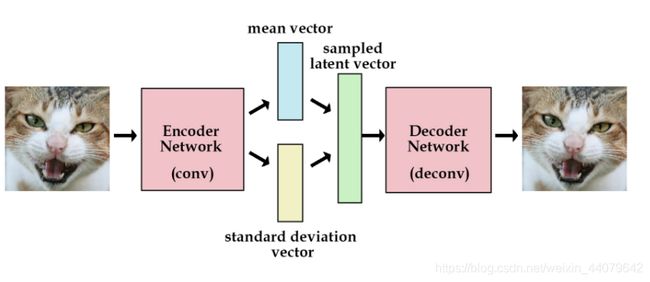
  更明确的流程图见下，源自《Tutorial on Variational Autoencoders》：
  VAE作为一种生成模型，用于在latent space上调整不同的属性来生成不同的输出。

生成对抗网络GAN

  本段只简单介绍GAN网络的特点和简单的算法，具体的理解本文暂不介绍和分析。
  若想了解GAN，可以参考李宏毅老师的GAN网络课程。

  以下两段摘自维基百科：
  “生成对抗网络（Generative Adversarial Networks）是非监督式学习的一种方法，通过让两个神经网络相互博弈的方式进行学习。该方法由伊恩·古德费洛等人于2014年提出。生成对抗网络由一个生成网络与一个判别网络组成。生成网络从潜在空间（latent space）中随机取样作为输入，其输出结果需要尽量模仿训练集中的真实样本。判别网络的输入则为真实样本或生成网络的输出，其目的是将生成网络的输出从真实样本中尽可能分辨出来。而生成网络则要尽可能地欺骗判别网络。两个网络相互对抗、不断调整参数，最终目的是使判别网络无法判断生成网络的输出结果是否真实。
  虽然生成对抗网络原先是为了无监督学习提出的，它也被证明对半监督学习、完全监督学习、强化学习是有用的。”
  生成模型是一种自下而上的模型，容易生成更深一层的模型，但是容易忽略掉生成节点之间的关系。
  判别模型作为一种自下而上的模型，考虑到了模型总体的情况，即各部分之间的关系，但是生成负样本时并不简单，特别是模型很复杂时，生成的负样本在短时间内并不会改善。
  GAN结合了生成模型和判别模型各自的特点，清晰易懂，结构合理，正是这样的特点为14年之后的GAN的广泛应用做了铺垫。
下面简要概括一下GAN的算法：
In each training iteration:
——————————discriminator——————————
Sample m examples $\{x^1,x^2,\cdots ,x^m\}$from database
Sample m noise samples $\{z^1,z^2,\cdots ,z^m\}$ from a distribution
Obtaining generated data $\{{\tilde{x}}^1,{\tilde{x}}^2,\cdots ,{\tilde{x}}^m\}$, ${\tilde{x}}^i=G(z^i)$
Update discriminator parameters θ_d to maximize:
$V=\frac{1}{m}{\sum }_{i=1}^{m}logD(x^i)+\frac{1}{m}{\sum }_{i=1}^{m}logD(1-{\tilde{x}}^i)$
${\theta }_d\leftarrow {\theta }_d+\eta \nabla V({\theta }_d)$
——————————generator——————————
Sample m noise samples$\{z^1,z^2,\cdots ,z^m\}$ from a distribution
Update generator parameters ${\theta }_g$ to maximize:
$V=\frac{1}{m}{\sum }_{i=1}^{m}logD(G(z^i))$
${\theta }_g\leftarrow {\theta }_g+\eta \nabla V({\theta }_g)$

VAE/GAN

主要贡献

译自原论文：
1.我们将VAEs和GANs合并成一个无监督生成模型，同时学习编码、生成和比较（判别）数据集样本。
2.我们证明了用学习相似性度量（similarity measure）训练的生成模型比用元素误差度量（element-wise error）训练的生成模型生成的图像样本更好。
3.我们证明了无监督训练的结果是一个潜在的图像表征，通过对带有视觉属性向量的人脸图像数据集的实验说明了这一点。实验表明，将简单的算法应用到学习的潜在空间中，可以生成反映这些属性变化的图像。

关于第二点的理解：
 VAE中用了L2损失来计算图片的重构误差，相应的需要最小化MSE，这种误差的人工选择方式，很大程度上决定了VAE在图像重建方面的效果总是模糊的。
  然而，GAN没有对最终损失函数的形式做任何假设。相反，它使用一个判别器来告诉我们样本是否来自期望的概率分布。来自判别器的信号(它使正负样本之间的交叉熵最小化)被反馈给生成器，然后生成器学习生成更好的样本。同样地，判别器也被串联地训练。这里的巧妙之处在于，GAN不会因为提出了一个人工设想的损失函数(如L1或L2损失)而受损，这种损失在数据中出现的复杂分布中可能是不足够准确衡量误差的。这就是为什么GANs能够产生看起来更清晰的样本的原因之一。
  因为VAE的bottleneck和GAN的input均为latent space，作者将VAE和GAN连接起来，Decoder便可作为GAN的generator。同时优化Encoder，Decoder（Generator）和Discriminator，使得encoder生成的latent space尽可能满足标准高斯分布，即图中的p（z），使得VAE前后的图片尽可能相似，即Decoder（generator）生成的图片尽可能real，使得Discriminator尽可能分辨出real和fake的图片。

该网络的简单算法实现如下：
Initialize $En,De,Dis$
In each iteration:
Sample M images$\{x^1,x^2,\cdots ,x^M\}$ from database
Generate M codes$\{z^1,z^2,\cdots ,z^M\}$ from encoder ${\tilde{z}}^i=En(x^i)$
Generate M images $\{{\tilde{x}}^1,{\tilde{x}}^2,\cdots ,{\tilde{x}}^M\}$ from decoder ${\tilde{x}}^i=De({\tilde{z}}^i)$
Sample M codes $\{z^1,z^2,\cdots ,z^M\}$ from prior $P(z)$
Generate M images $\{{\hat{x}}^1,{\hat{x}}^2,\cdots ,{\hat{x}}^M\}$ from decoder ${\hat{x}}^i=De({\tilde{z}}^i)$
Update $En$ to decrease $\Vert {\tilde{x}}^i-x^i\Vert$, decrease $KL(P({\tilde{z}}^i|xi)\Vert P(z))$
Update $De$ to decrease $\Vert {\tilde{x}}^i-x^i\Vert$, increase $Dis({\tilde{x}}^i)$ and $Dis({\hat{x}}^i)$
Update $Dis$ to increase $Dis(x^i)$, decrease $Dis({\tilde{x}}^i)$ and $Dis({\hat{x}}^i)$

实验结果

  本论文所用数据集为CelebA face images，作者分别用了VAE，VAE/GAN，GAN对人脸进行了生成和重建，对比了效果，直观感受VAE/GAN效果最好。

  然后作者对latent space上的每一个维度所对应着特定的可视的属性，如：口红，刘海，胡须等，进行了可视化和一些有趣的调整。

  进一步，作者为了寻求对生成的图像进行更定量的评价标准，采用Labeled faces in the wild (LFW) images with attributes数据集， 学习基于面部属性的面部图像生成模型。
  在测试时，从所选择的属性配置中检索出人脸图像，并让一个单独训练的回归网络从所生成的图像中识别属性，根据属性识别的误差来量化三种方法的效果。


  最终结果显示，与一般的VAE相比，VAE/GAN模型具有更好的识别性能，属性的存在性和误差都是更加优秀的。

总结

  本论文从VAE出发，巧妙地将自动编码器和生成对抗网络结合，从loss的根源分析并且用实验证明了VAE/GAN网络的优越性。

参考资料

1.Anders Boesen, Lindbo Larsen, Søren Kaae Sønderby, Hugo Larochelle, Ole Winther“Autoencoding beyond pixels using a learned similarity metric” , ICML. 2016
2.Kingma, Diederik P., and Max Welling. “Auto-encoding variational bayes.” arXiv preprint arXiv:1312.6114 (2013).
3.CARL DOERSCH Carnegie Mellon / UC Berkeley “Tutorial on Variational Autoencoders” August 16, 2016
4.VAE(Variational Autoencoder)的原理
5.李宏毅深度学习课程