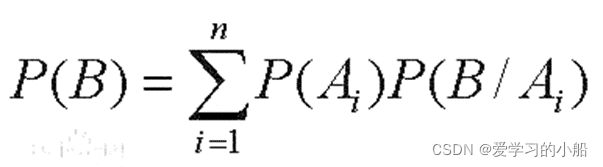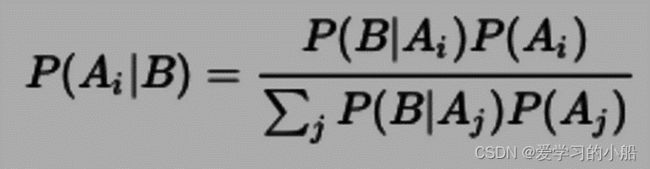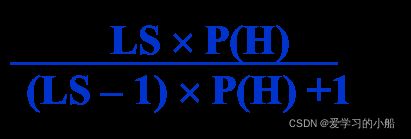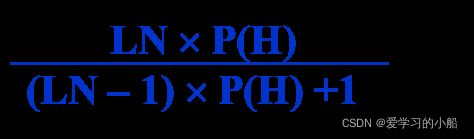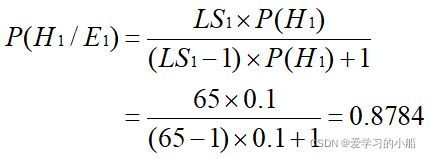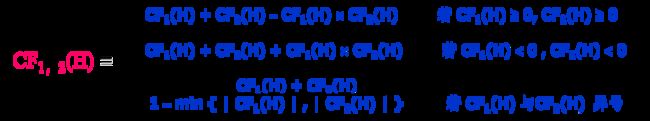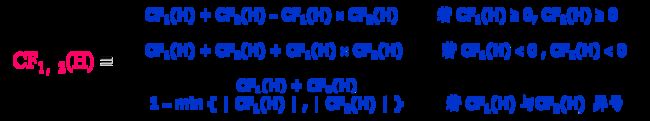《人工智能及其应用》课程笔记(四)第4章 非经典推理
目录
本章内容
4.1 经典推理和非经典推理
4.2 不确定性推理
4.2.1 不确定性的表示和度量
4.2.2 不确定性的算法
4.3 概率推理
4.3.1 概率的基本性质和计算公式
4.4 主观贝叶斯方法
4.4.1 知识不确定性的表示
4.4.2 证据不确定性的表示
4.4.3 主观贝叶斯方法的推理过程
4.5 可信度方法
4.5.1 基于可信度的不确定性表示
4.5.2 可信度方法的推理算法
重要公式总结:
本章内容
熟悉经典推理和非经典推理的区别
掌握不确定推理的基本概念
掌握概率推理方法
掌握主观贝叶斯推理方法
掌握可信度推理方法
了解证据理论的基本知识
4.1 经典推理和非经典推理
非经典推理和经典推理的区别表现在:
推理方法。经典采用演绎逻辑推理,非经典采用归纳逻辑推理。
辖域取值。经典逻辑都是二值逻辑,非经典是多值逻辑。
运算法则。经典逻辑中的许多法则在非经典逻辑中不成立。
逻辑算符。非经典逻辑具有更多的逻辑算符。
是否单调。经典逻辑单调,而非经典逻辑是非单调逻辑。
4.2 不确定性推理
不确定性推理是一种建立在非经典逻辑基础上的基于不确定性知识的推理,从不确定性的初始证据出发,通过运用不确定性知识,推出具有一定程度的不确定性的和合理的或近乎合理的结论。
不确定性推理中必须解决推理方向、推理方法、控制策略等基本问题,同时还需要解决不确定性的表示与度量、不确定性匹配、不确定性的传递算法以及不确定性的合成等问题。
4.2.1 不确定性的表示和度量
1、不确定性及其类型:
①随机不确定性,eg: 这场比赛A队可能获胜
②模糊不确定性,eg:小明是个高个子
③不完全性,eg:刑侦过程的某些阶段往往要针对不完全的证据进行推理
④不确定性,eg:人们对太空的认识
2、三种不确定性:
①关于知识的不确定性
②关于证据的不确定性
③关于结论的不确定性
3、知识的表示与推理密切相关,不同的推理方法要求有相应的知识表示模式与之对应
4、知识的度量
静态强度:专家系统中通常用一个数值表示相应知识的不确定性程度
动态强度:证据的不确定性也通常用一个数值代表相应证据的不确定性程度
4.2.2 不确定性的算法
1、不确定性的更新算法:
(1)已知规则前提即证据E的不确定性C(E)和规则的强度f(H,E),其中H表示假设,求H的不确定性C(H)
(2)并行规则算法
(3)证据合取的不确定性算法
(4)证据析取的不确定性算法
证据析取、证据合取的不确定性算法统称为组合证据的不确定性算法
2、不确定性的计算与传播:
(1)组合证据的不确定性计算(最大最小方法、概率方法、有界方法)
(2)证据和知识的不确定性的传递
(3)不同证据支持同一结论时其不确定性的合成
不确定性推理的一般模式也可以简单地表示为:
不确定性推理=符号推演+不确定性计算
3、不确定性方法的分类:
4.3 概率推理
4.3.1 概率的基本性质和计算公式
1、统计概率的性质:
(6)对任一事件A,有:
P(![]() ) =1-P(A)
) =1-P(A)
![]() 表示事件A的逆,即事件A和事件A的逆 有且仅有一个发生
表示事件A的逆,即事件A和事件A的逆 有且仅有一个发生
2、概率的部分计算公式
(1)条件概率与乘法公式:
P(A|B)=P(A∩B)/P(B)
(2)独立性公式:
若事件满足 P(A|B)=P(A),则称事件A关于事件B是独立的,A与B相互独立的充要条件:
P(A∩B)= P(A)P(B)
(3)全概率公式:
(4)贝叶斯公式:
4.4 主观贝叶斯方法
核心思想:
根据 先验概率 (H出现的概率 P(Hi) )以及证据E的 条件概率 (Hi出现的情况下E出现的概率 P(E | Hi)) 得到后验概率(出现E的情况下出现Hi的概率)
例如:
小明去上学,坐公交车迟到的概率是30%,步行迟到的概率是20%,假设选择每种公交车的可能性相同,问小明迟到了,坐公交车的可能性是多少?
4.4.1 知识不确定性的表示
1、主观贝叶斯方法用产生式规则表示知识:
if E then (LS, LN) H
(LS,LN) 表示该知识的静态强度
LS为上式成立的充分性因子,衡量证据 E 对结论 H 的支持程度
LN为上式成立的必要性因子,衡量 ~E 对 H 的支持程度
LS 和 LN 的取值范围是 [0,+∞),由领域专家给出
E 是该条知识的前提条件,它既可以是一个简单条件, 也可以是用and 、or 把多个条件连接起来的复合条件。
H 是结论,P(H) 是 H 的先验概率,它指出在没有任何专门证据的情况下,结论为真的概率,其值由领域专家根据以往的实践及经验给出
2、推理过程即为根据前提 E 的概率 P(E),利用规则的 LS 和 LN,把结论 H 的先验概率 P(H) 更新为后验概率 P(H|E) 的过程
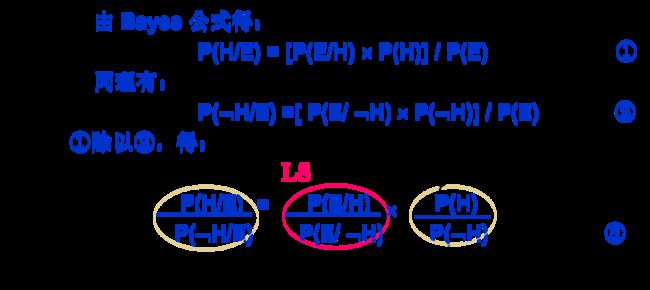
3、在贝叶斯方法中,引入概率函数O(x),表示事件x发生的概率与不发生的概率之比,把x发生概率的取值从[0,1]放大到[0,+∞)
4、更新贝叶斯公式:
1)对于LS:
由③式得到 O(H/E)=LS×O(H) (该公式被称为Bayes公式的几率似然性形式,LS为充分似然性)
由③ 式 及 “非”运算 :P( ~H/E) = 1 – P(H/E) 、 P( ~H) = 1 – P(H), 得:
![]()
2)对于LN:同理 O(H/ ~E)=LN×O(H)
![]()
附 LS和LN的性质
-当证据E越是支持H为真时,LS的值越大
-当证据E对H重要时,则LN值应该越小
4.4.2 证据不确定性的表示
对于初始证据 E ,由用户根据观察 S 给出 P(E/S),它相当于动态强度
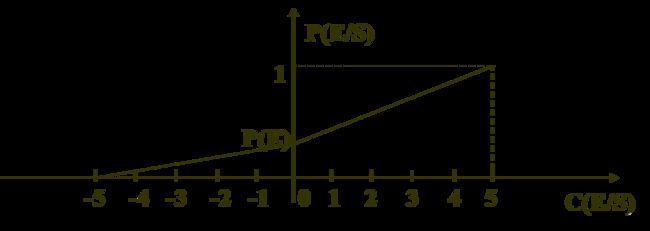
用C(E/S)刻画证据的不确定性。 让用户在 –5 至 5 之间的 11 个整数中选一个数作为初始证据的可信度C(E/S)
初始可信度 C(E/S) 与 概率 P(E/S) 的对应关系如下:
C(E/S)= -5 ,表示在观察 S 下证据 E 肯定不存在,即 P(E/S)=0;C(E/S)= 0 , 表示 S 与 E 无关,即 P(E/S) =P(E) ;C(E/S)= +5 ,表示在观察 S 下证据 E 肯定存在,即 P(E/S)=1;C(E/S) = 其它数值时,与 P(E/S) 的对应关系可通过对上述三点进行 分段线性插值 得到,如下图。
在证据不确定的情况下,不能再用上面利用LS和LN的公式计算后验概率,而需使用 R.O.Doda 等人1976年证明的如下公式:
P(H | S) = P(H | E)×P(E | S) + P(┐H | E) × P(┐E | S) ①
分四种情况讨论:
1)P(E/S) = 1
当 P(E/S) = 1 时, P(┐E/S) = 0,此时公式 ① 变为:
这是证据肯定存在的情况。
2)P(E/S) = 0
当 P(E/S) = 0 时, P(┐E/S) = 1,此时公式 ① 变为:
这是证据肯定不存在的情况
3)P(E/S) = P(E)
当 P(E/S) = P(E) 时,此时公式 ① 变为:
表示H与S无关
4)当 P(E/S) = 其它值时,通过分段线性插值可得到计算P(H/S)的公式,EH公式
对初始证据,用可信度C(E/S) 计算P(H/S),该公式为CP公式
![]()
4.4.3 主观贝叶斯方法的推理过程
若采用初始证据进行推理,则通过用户得到C(E|S),从而根据CP公式可求得 P(H|S)
若采用推理过程中得到的中间结论作为证据进行推理,则通过 EH 公式可求得 P(H|S)。
例:设有如下规则
r1: IF E1 THEN (65, 0.01) H1
r2: IF E2 THEN (300, 0.001) H1
r3: IF H1 THEN (200, 0.002) H2
已知: P(E1)=0.1 ,P(E2)=0.03, P(H1)=0. 1 ,P(H2)=0.05,用户提供证据:C(E1/S1)=2,C(E2/S2)=1,计算P(H2/S1,S2)
分析:自下而上计算:
根据LS值,将H的先验概率转换为后验概率,计算P(H1/E1)、P(H1/E2)使用CP公式计算P(H1/S1)、P(H1/S2) ,计算O(H1/S1)、O(H1/S2)对H1合成。计算 O(H1/S1,S2)、P(H1/S1,S2) 。根据LS值,将H的先验概率转换为后验概率,计算P(H2/H1)使用EH公式计算P(H2/S1,S2)
(1)计算 P(H1/E1) 、P(H1/S1) 和 O(H1/S1)
对于初始证据,使用CP公式:
(2)同理,计算P(H1/E2)、 P(H1/S2)和 O(H1/S2)
(3)计算O(H1/S1,S2)和 P(H1/S1,S2)
(4)计算 P(H2/H1)和 P(H2/S1,S2)
使用EH公式,∵ P(H1/S1,S2)> P(H1) ∴ 使用EH公式的后半部。
4.5 可信度方法
4.5.1 基于可信度的不确定性表示
推理规则的一般形式:
If E then H (CF(H , E))
其中 CF(H , E) 是该规则的可信度,称为可信度因子或规则强度。
CF(H , E) >0表示该证据增加了结论为真的程度,且CF(H , E)的值越大则结论 H 越真;若CF(H , E) =1,则表示该证据使结论为真。
CF(H , E) <0 表示该证据增加了结论为假的程度,且CF(H , E)的值越小则结论 H 越假;若CF(H , E) =-1则表示该证据使结论为假。
CF(H , E) =0 表示证据 E 和结论 H 没有关系。
CF(H,E)的计算公式:
![]()
4.5.2 可信度方法的推理算法
1、组合证据(前提证据事实总CF值计算,最大最小法)
(1)合取证据:多个证据的合取(与),取最小
(2)析取证据:多个证据的析取(或),取最大
![]()
2、推理结论的CF值计算
结论 H 的可信度由下式计算:
CF(H) = CF(H,E) × max { 0, CF(E) }
3、重复结论CF值计算(多个独立证据推出同一假设的合成算法)
if E1 then H (CF(H, E1))
if E2 then H (CF(H, E2))
(1)计算CF1(H) CF2(H);
(2)计算CF (H):
例: 设有如下规则:
r1: IF E1 THEN H ( 0.8)
r2: IF E2 THEN H (0.9)
r3: IF E3 AND E4 THEN E1 (0.7)
r4: IF E5 OR E6 THEN E1 (-0.3)
并已知初始证据的可信度为:CF(E2)=0.8,CF(E3)=0.9,CF(E4)=0.7,CF(E5)=0.1,CF(E6)=0.5,用不确定性理论计算CF(H)。
解:
由r3可得: CF1(E1)=0.7×min{0.9,0.7}=0.49
由r4可得: CF2(E1)=-0.3×max{0.1,0.5}=-0.15
从而 CF1,2(E1)=(0.49-0.15)/(1-min(|0.49|,|-0.15|))=0.34/0.85=0.4
由r1可得: CF1(H)=0.4×0.8=0.32
由r2可得: CF2(H)=0.8×0.9=0.72
从而 CF1,2(H)=0.32+0.72-0.32×0.72=0.8096
这就是最终求得的H的可信度。
重要公式总结:
1 全概率公式:
2 贝叶斯公式:
3 几率函数计算方法:
4 利用LS、LN将H先验概率更新为后验概率
5 证据不确定的情况下,计算后验概率:
6、 EH公式:
7 CP公式:
8 组合证据:最大最小法计算前提事实总CF值(and取最小,or取最大)
9 推理结论的CF值计算
CF(H) = CF(H,E) ´ max { 0, CF(E) }
10 重复结论CF值计算