数据科学导论学习小结——其三

数据科学导论学习小结——其三

这是笔者大学二年级必修科目《数据科学基础》个人向笔记整理的第三部分，包含第六、第七两个章节。本笔记内容基于清华大学出版社《数据科学导论-探索数据的奥秘》的相关知识。对于同样学习本门学科的读者可以此做参考方便您的学习；对于其他对本学科或相关领域感兴趣的读者，也可以在对本篇的阅读中激发兴趣。

---

---

第六章 建模与性能评价

本篇章包含大量概率论与数理统计的内容，教材包括博主在此只做最基本的介绍。想要详细学习本部分知识的读者可以参考站内其他博主的博文或其他相关教材

6.1 统计建模

统计建模的实质：描述统计+推断统计（参数估计、假设检验）

（1）基本概念回顾

概率分布函数F(x)：给出取值小于某个值的概率，是概率的累加形式
概率密度函数f(x)：给出了变量落在某值邻域内（或者某个区间内）的概率变化快慢，概率密度函数的值不是概率，而是概率的变化率，概率密度函数下面的面积才是概率

（2）常见的概率密度函数

概率密度函数PDF：$f(x)$用来表示连续随机变量落在各值附近的可能性，给定$f(x)$后，X的一次抽样落入某区间的概率就等于概率密度函数$f(x)$在该区间上的积分，即
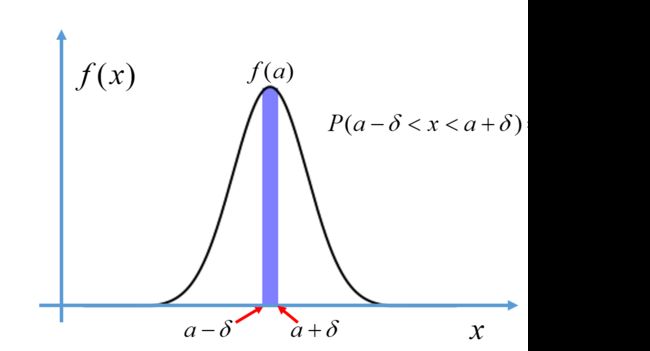
$$p(a-\delta <x<a+\delta )={\int }_{a-\delta }^{a+\delta }f(x)dx$$

$f(x)$的性质：
①在$x$的定义域上，$f(x)\ge 0$
②${\int }_{-\infty }^{+\infty }f(x)dx=1$
由概率密度函数可以给出随机变量的发布特征，常见的有正态分布、t分布、卡方分布等

①正态分布（高斯分布）：概率密度函数为
$$f(x)=\frac{1}{\sqrt{2\pi }\sigma }{e}^{\frac{(x-\mu {)}^2}{2{\sigma }^2}}$$
其中$\mu$表示均值，$\sigma$表示标准差
随机变量$X$服从正态分布，记为：$X\to N(\mu ,{\sigma }^2)$
均值为0，标准差为1时服从标准正态分布，记为$X\to N(0,1)$

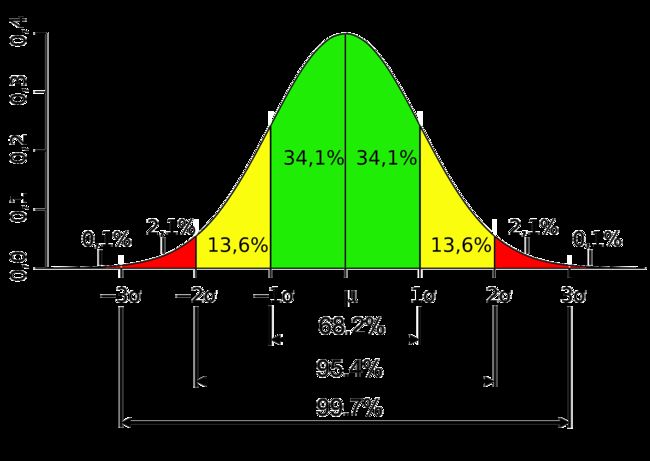
正态分布几个特点：
Ⅰ.均值就是期望
Ⅱ.极端值少
Ⅲ.标准差决定胖瘦（标准差大则矮胖，标准差小则瘦高）
相关定理：
Ⅰ.中心极限定律：当样本容量足够大时，独立随机样本的叠加会更加趋向于正态分布。设$x_1$，…，$x_n$是某一个均值$\mu$,标准差$\sigma$的总体的相互独立随机样本，则当样本容量足够大（如$n\ge 30$），无论总体分布是否为正态分布，都有统计平均$\bar{X}\to N(\mu ,\frac{{\sigma }^2}{n})$。大样本均值估计的依据：从总体中抽样，每组样本容量大于等于30时，样本均值符合正态分布，以此可做均值的点估计和区间估计
Ⅱ.切比雪夫大数定律：随着样本(不要求同分布)容量n的增加，样本平均数将接近于总体平均数

②t分布（学生t分布）：根据小样本来估计呈正态分布且方差未知的总体均值。样本容量小于30时，样本均值不符合正态分布，则可以将均值标准化后构造一个统计量t，统计量t是符合t分布的，在t分布中做均值估计和区间估计
构造统计量t：
$$t=\frac{\bar{x}-\mu }{\frac{s}{\sqrt{n}}}$$

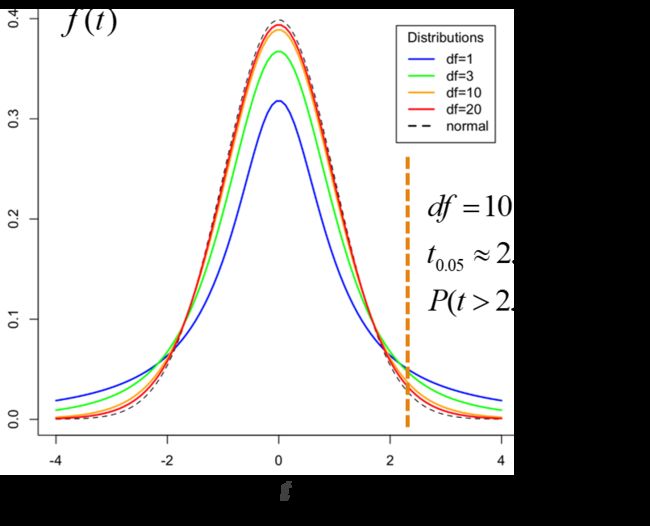
t分布的概率密度函数是由自由度$df$控制的一簇曲线，t分布的自由度是样本容量$n-1$，曲线关于$t=0$对称，样本容量越小，曲线越平坦；样本容量越大，曲线越接近正态分布。小样本均值估计依据

③卡方分布：设$x_1$，…，$x_n$是来源于服从标准正态分布$N(0,1)$潜在总体的$n$个独立随机抽样，则对于构造统计量${\chi }^2$
$${\chi }^2=\sum _{i=1}^n{x}_i^2$$
服从自由度为$n$的卡方分布

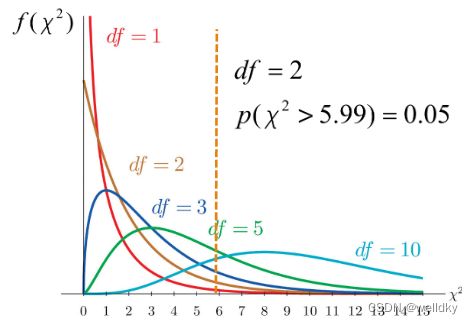
卡方分布的曲线是一簇由自由度$df$控制的曲线，随着$df$的增加，曲线的最大值逐渐向统计量${\chi }^2$更大的方向移动。方差区间估计的依据

（3）参数估计

参数估计：基于样本统计量$X$/$E(X)$或$s$而对总体分布参数$\mu$或$\sigma$进行估计
①均值点估计：依据中心极限定律，来源于同一总体的独立随机抽样的算术平均服从均值$\mu$的正态分布，所以样本的统计均值就是总体均值的无偏估计，记为：
$$E(\bar{X})=\mu$$

均值点估计代码举例：

from random import sample
import numpy as np
import pandas as pd
from scipy import stats # python的stats模块提供了大量统计学常用函数

np.random.seed(1234) # 设置随机数种子方便实验结果的复现
my_data1 = stats.poisson.rvs(loc = 10, mu = 60, size = 3000) # 生成一个规定均值的泊松分布
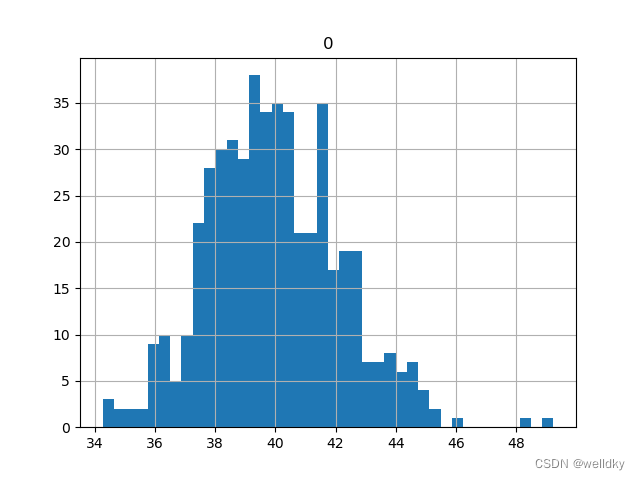
pd.Series(my_data1).hist().get_figure().show # 作直方图展示
print("第一个均值分布是:70,\t统计平均是:", my_data1.mean()) # 均值人为规定，统计平均直接计算，看是否和指定的均值一致
my_data2 = stats.poisson.rvs(loc = 10, mu = 15, size = 6000)
pd.Series(my_data1).hist().get_figure().show
print("第一个均值分布是:25,\t统计平均是:", my_data2.mean())
my_data = np.concatenate((my_data1, my_data2)) # numpy.ndarray对象的连接
print("总体的均值为:", my_data.mean())
sample_data = np.random.choice(a = my_data, size = 100) # 从总体中取100个样本计算样本均值
print("样本的均值为:", sample_data.mean())

'''
	输出结果
	第一个均值分布是:70,    统计平均是: 69.97966666666666
	第一个均值分布是:25,    统计平均是: 25.009333333333334
	总体的均值为: 39.99944444444444
	样本的均值为: 39.3
'''

以上代码用到的具体方法：
np.random.seed( )方法：用于指定随机数生成时所用算法开始的整数值，如果使用相同的值，则每次生成的随机数都相同
np.concatenate( )方法：用于连接 np.ndarray 对象
pd.Series( )方法：将一个列表、np.ndarray 对象转化为 pandas.Series 对象
np.random.choice( a, size = )方法：从a随机抽取数字，并组成指定 size 的数组
具体参数：
a np.ndarray 对象
size 整数 指定抽取样本的个数

stats.poisson.rvs( loc = , mu = , size = )方法：从泊松分布中生成指定个数的随机数，rvs 表示产生服从指定分布的随机数
具体参数：
loc 与 mu 两者共同决定这个分布的均值（两者之和）
size 整数 生成随机数的个数

从图中可以看出：样本的统计平均与总体均值虽然不是完全相等，但已经相当接近
表示：用样本统计平均$\bar{X}$作为总体均值$\mu$的点估计

TIP：利用相关方法还可以对中心极限定律进行验证

以下代码连接于上个代码之后，用于验证中心极限定律：

point_estimates = [] # 一个列表，用于存放每次抽样的样本均值
for x in range(500):
    sample = np.random.choice(a = my_data, size = 100) # 抽取100个样本
    point_estimates.append(sample.mean()) # 计算样本的均值并存入列表
pd.DataFrame(point_estimates).hist(bins = 40) # 将列表转换为pandas.DataFrame对象后画直方图展示
print("样本均值的均值为:", np.array(point_estimates).mean()) # 将列表转化为np.ndarray对象后可以利用mean()方法计算平均值

'''
	输出结果
	样本均值的均值为: 39.95712
'''

从图中可以看出：样本的均值趋向于正态分布

②均值区间估计：对于总体进行的独立随机抽样，样本均值会分布在一个范围里，对于一个给定的置信水平，就可以求得一个置信区间

以下代码连接于上个代码之后：均值区间估计代码举例：

sample = np.random.choice(a = my_data, size = 100)
sigma = sample.std()/(sample_size) ** 0.5 # 构造t统计量的分母
print(stats.t.interval(alpha = 0.95, df = sample_size - 1, loc = sample.mean(), scale = sigma)) # 求置信区间

'''
	输出结果
	(36.29263468910625, 45.26736531089375)
'''

以上代码用到的方法：
stats.t.interval( alpha = , df = , loc = , scale = )方法：用于针对t分布求置信区间
具体参数如下
alpha 浮点数 代表置信水平
df 整数 代表t分布的自由度，一般取样本容量-1
loc 浮点数 代表构造t统计量需要的样本均值
scale 浮点数 代表构造t统计量需要的分母sigma

以上代码得到的结果是置信区间，表示该区间内有95%概率包含了总体均值
③方差估计：假设$n$个随机样本来源于均值$\mu$，方差${\sigma }^2$的总体，则由公式：
$$s^2=\frac{1}{n-1}\sum _{i=1}^n(x_i-\bar{x}{)}^2$$
定义的样本方差是总体方差的无偏估计，即$E(s^2)={\sigma }^2$
TIP：卡方分布有潜在总体服从N(0,1)分布的前提要求

（4）假设检验

通常做法是：提出一个假设，验证是否可以接受该假设

假设检验的基本思想：反证法
在假定某个假设是正确的情况下构造一个小概率事件，如果在一次试验里小概率事件发生了，则拒绝这个假设

假设检验的相关概念：
Ⅰ空假设\零假设：待检验的假设，用$H_0$表示（一般事物的惯常态，概率大）
TIP：常见的零假设：总体的均值等于μ；测试组和对照组来源于均值相等的总体；控制因素对观察变量没有影响，A组和B组数据同分布

Ⅱ替代假设\备择假设：空假设的对立，用$H_1$表示（概率小）
TIP：常见的备择假设：总体的均值不等于μ；测试组和对照组来源于均值不等的总体；控制因素对观察变量有影响，A组和B组数据不同分布

Ⅲ显著性水平：统计检验时需要将从样本获取的统计量与显著性水平比较（p值与alpha值的比较），一般人为定义（取0.05）

假设检验的一般步骤：
①确定总体和sample size（适中）
②收集数据
③确定$H_0$和$H_1$
④设置显著性水平alpha
⑤选择并计算相应的统计量，进行假设检验
⑥根据统计量或假设检验的p值与显著性水平的比较决定拒绝或接受$H_0$

假设检验的两类错误：

判定	真实性$H_0$	真实性$H_1$
接受$H_0$	正确	Ⅱ型错误
接受$H_1$	Ⅰ型错误	正确

假设检验类型：
①t检验—均值的单样本检验：对单组样本的均值进行假设检验
t检验：借助t统计量服从t分布
Ⅰ.单样本双边均值检验：
假设$H_0$：总体均值等于$\mu$
对应$H_1$：总体均值不等于$\mu$
Ⅱ.单样本单边均值检验：将不等于换成大于或小于

单样本双边均值检验代码举例：

import numpy as np
import pandas as pd
from scipy import stats
import matplotlib.pyplot as plt
from scipy.stats import t # t检验

# 生成一个含有9000样本的总体
np.random.seed(1234)
my_data1 = stats.poisson.rvs(loc = 10, mu = 60, size = 3000)
my_data2 = stats.poisson.rvs(loc = 10, mu = 15, size = 6000)
my_data = np.concatenate((my_data1, my_data2))

# 假设
print("空假设H0是:总体的均值是47.5\n") # 假设的总体均值可由(70+25)/2得来

# 检验
sample_data = np.random.choice(a = my_data, size = 100) # 抽样
t_statistic, p_value = stats.ttest_1samp(a = sample_data, popmean = 47.5) # 计算得到t统计量和p值
print("从样本构造的t统计量 = ", t_statistic)
print("p = ", p_value)

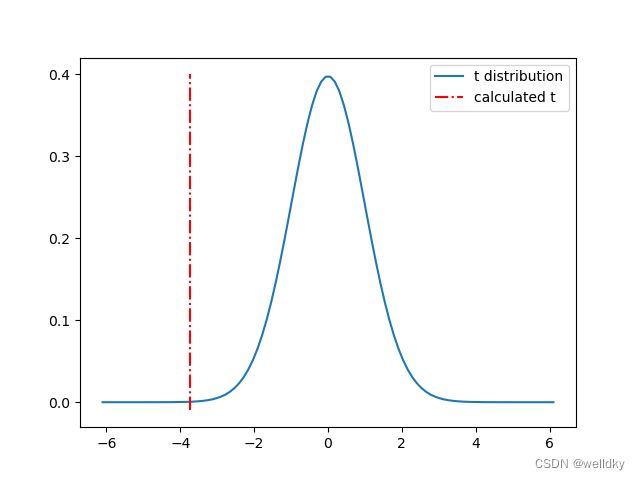
# 画出t分布图像
df = 100 - 1 # 设置自由度
x = np.linspace(stats.t.ppf(0.00000001, df), stats.t.ppf(0.99999999, df), 100)
plt.plot(x, t.pdf(x, df))
plt.plot((t_statistic, t_statistic), (-0.01, 0.4), "-.r")
str_legend = ("t distribution", "calculated t")
plt.legend(str_legend)
plt.show()

'''
	输出结果
	空假设H0是:总体的均值是47.5
	从样本构造的t统计量 = -3.7405281096559153
	p = 0.00030786517310847877
'''

以上代码用到的具体方法：
stats.ttest_1samp( a = , popmean = )方法：返回a样本集的t统计量与p值，一般用两个变量t_statistic和p_value去接收
具体参数：
a np.ndarray 对象 代表样本集
popmean 浮点数 代表零检验中的期望值

np.linspace(start, end, num = )方法：用于在线性空间中以均匀步长生成数字序列
具体参数：
start 范围起始
end 范围结束
num 序列中的总点数

stats.t.ppf( )方法：用来求分位点（在图像中确定了曲线边界）
stats.t.pdf( )方法：用来生成概率密度函数表（在图像中对应了纵坐标）

plt.legend( legend = )方法：用于定义图例
具体参数：
legend 元组 内含图例的名字

以上图片理解为：如果总体均值是47.5，则其中的100个独立随机抽样构造出的t统计量会服从曲线所示的概率分布，图中的点划线就是现在这100个随机抽样的样本的t统计量在曲线上的位置（可见：较远偏离曲线中心），t统计量绝对值越大越偏离曲线的中心；p值代表t统计量外曲线下面积
将p值与alpha值进行比较，如果$p\le alpha$，则拒绝$H_0$

以下代码连接于上个代码之后：判断是否要拒绝$H_0$

alpha = 0.05 # 人为定义alpha值
if p_value > 0.05:
    print("接受 H0")
else:
    print("拒绝 H0, 即总体的均值不等于47.5, 此时错误拒绝H0的概率为", p_value, "小于显著性水平")

'''
	输出结果
	拒绝 H0,即总体的均值不等于47.5, 此时错误拒绝H0的概率为0.00030786517310847877 小于显著性水平
'''

如上例可知假设检验存在风险，存在两类错误，如上介绍

②t检验—均值的双样本检验：两组数据间的均值比较
t检验：借助t统计量服从t分布
假设$H_0$：两组样本的潜在总体均值相等（${\mu }_1={\mu }_2$）
对应$H_1$：两组样本的潜在总体均值不相等（${\mu }_1\ne {\mu }_2$）
当两组潜在总体方差相等时，构造t统计量
$$t=\frac{\overline{X_1}-\overline{X_2}}{S_p\sqrt{\frac{1}{n_1}+\frac{1}{n_2}}}$$
其中，$Sp=\sqrt{\frac{(n_1-1){S_X}_1^2+(n_2-1){S_X}_2^2}{n_1+n_2-2}}$，t分布的自由度$df$为$(n_1+n_2-2)$，此时应该使用stats.ttest_ind
当两组潜在总体方差不相等时，构造t统计量
$$t=\frac{\overline{X_1}-\overline{X_2}}{S_e}$$
其中，$Se=\sqrt{\frac{{S_X}_1^2+{S_X}_2^2}{n}}$，t分布的自由度$df$为$(n-1)$，此时应该使用stats.ttest_rel

双样本均值检验代码举例：

import numpy as np
import pandas as pd
from scipy import stats
import matplotlib.pyplot as plt
from scipy.stats import t

# 构造一个总体
np.random.seed(1234)
my_data1 = stats.poisson.rvs(loc = 10, mu = 60, size = 3000)
my_data2 = stats.poisson.rvs(loc = 10, mu = 15, size = 6000)
my_data = np.concatenate((my_data1, my_data2))

# 构造两组样本，存放于字典
my_sample = {}
for n in range(2):
    my_sample[n] = np.random.choice(a = my_data, size = 100)
    print("第", n, "组样本的均值为",my_sample[n].mean())

# 双样本均值检验
alpha = 0.01 # 人为规定置信水平
t_statistic, p_value = stats.ttest_rel(a = my_sample[0], b = my_sample[1]) # 计算得到t统计量和p值（这里假设不知道总体的方差是否相等，所以优先取用ttest_rel方法）
print("t = ", t_statistic)
print("p = ", p_value)
if p_value <= alpha:
    print("拒绝 H0:两样本来源的总体均值相等")
else:
    print("接受 H0:两样本来源的总体均值相等")

'''
	输出结果
	第 0 组样本的均值为 39.3
	第 1 组样本的均值为 41.14

	t =  -0.5797156447793128
	p =  0.5634233550606107
	接受 H0:两样本来源的总体均值相等
'''

③z检验：当样本容量大于30或样本容量小于30但已知潜在总体服从正态分布时，t分布由正态分布取代，t检验也由z检验取代

④卡方检验：研究两组类别型数据在某一特征上的概率分布是否一致时，通常利用卡方检验
假设$H_0$：组A的分布与组B一致
对应$H_1$：组A与分布与组B不一致
举例：检验titanic数据中幸存者是否是女多男少时，则只需要比较幸存者在性别特征的两个分类别（男、女）的分布情况，则可以做出如下假设：
假设$H_0$:幸存者中的性别分布与船上所有人的性别分布一致
对应$H_1$:幸存者中的性别分布与船上所有人的性别分布不一致

卡方检验代码举例：

import numpy as np
import pandas as pd
from scipy import stats
from scipy.stats import chi2 # 卡方检验

titanic = pd.read_csv("titanic.csv")

# 计算船上所有人的男女比例
mask1 = titanic["Sex"] == "male" # 返回的是pandas.Series对象
mask2 = titanic["Sex"] == "female"
p = np.array([sum(mask1) / (sum(mask1) + sum(mask2)), sum(mask2) / (sum(mask1) + sum(mask2))])
print("船上的男女比例为:", p)

mask_survived = titanic["Survived"] == 1 # 返回的是pandas.Series对象，内含索引号与一个布尔类型，代表是否存活
my_survived = titanic.loc[mask_survived, 'Sex'] # 获取指定行，loc里面的mask_survived代表指定的行索引，'Sex'是需要获取的内容，得到的是pandas.Series对象，只含有行序号和性别
pop_size = my_survived.count()
print("存活的人共有:", pop_size)

E = pop_size * p
print("预期的男、女个数为:", E)

mask1 = my_survived == "male" # 得到一个pandas.Series对象，内含索引号与一个布尔类型，代表是否是男性
mask2 = my_survived == "female"
my_set1 = my_survived[mask1]
my_set2 = my_survived[mask2]
O = np.array([len(my_set1), len(my_set2)])
print("实际的男、女个数为:", O)

chi_squard, p_value = stats.chisquare(f_obs = O, f_exp = E) # 卡方检验，得到卡方统计量与p值
print("卡方检验的p = ", p_value)

a = 0.05 # 人为规定的置信水平
if p_value <= a:
    print("拒绝 男性、女性具有相同生存率的假设")
else:
    print("接受 男性、女性具有相同生存率的假设")

'''
	输出结果
	船上的男女比例为: [0.64758698 0.35241302]
	存活的人共有: 342
	预期的男、女个数为: [221.47474747 120.52525253]
	实际的男、女个数为: [109 233]
	卡方检验的p = 3.970516389658729e-37
	拒绝 男性、女性具有相同生存率的假设（逃生时确实做到女士优先）
'''

以上代码用到的具体方法：
stats.chisquare( f_obs = , f_exp = )方法：返回卡方统计量与p值，一般用两个变量chi_squard和p_value去接收
具体参数：
f_obs 数组 在每个类别中观察的频率
f_exp 数组 在每个类别中预期的频率

注意：python中用于stats假设检验的都是np.ndarray结构

（5）p-hacking

即便p 即便空假设成立，当随机尝试100种不同的特征时，出现5个落入拒绝域的特征也是完全合理的
避免过度挖掘数据——p-hacking（操作p值）

6.2 回归模型

回归指建立因变量y与自变量x之间的函数关系：
$$\hat{y}=f(x)$$
其中，$f$代表拟合的函数关系，$\hat{y}$代表用$f$获得的对$y$的估计（或预测）
回归分类：
一元回归：x只包含一个特征
多元回归：x包含多个特征
线性回归：函数关系$f$是线性的
非线性回归：函数关系$f$是非线性的

（1）线性回归模型：一元线性回归为例

建立因变量$y$与一维特征$x$的线性函数关系：
$$\widehat{y_k}={\beta }_0+{\beta }_1{x_k}_i$$
其中，${\beta }_0$代表截距，${\beta }_1$代表回归系数，$\widehat{y_k}$代表预测值，同时也有实际的$y$取值$y_k$代表观测值

线性回归模型的一些概念：
①残差：预测值和真实值之间差的绝对值
②残差平方和$S{S}_{residuals}$：$S{S}_{residuals}=\sum _{k=1}^n(\widehat{y_k}-y_k{)}^2$
使残差平方和最小：利用最小二乘法
③一元回归直线：使残差平方和最小的直线，且通过点$(\overline{x_1},\bar{y})$，其中$\overline{x_1}$，$\bar{y}$代表所有样本在特征$x_1$，$y$上的统计均值
④均方根误差RMSE：$RMSE=\sqrt{\frac{1}{n}\sum _{k=1}^n(\widehat{y_k}-y_k{)}^2}$，代表回归模型与观察值之间的总体误差

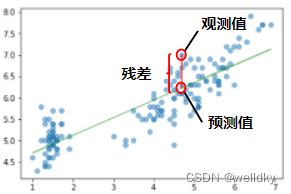
一元线性回归代码举例：

import numpy as np
import pandas as pd
from scipy import stats
from matplotlib import pyplot as plt
from sklearn import metrics
from sklearn.linear_model import LinearRegression # 线性回归需要导入的库
from torch import alpha_dropout

# 读取数据
my_iris = pd.read_csv("iris.csv", sep = ',', decimal = '.', header = None, names = ["sepal_length", "sepal_width", "petal_length", "petal_width", "target"])

x = my_iris[["petal_length"]] # 提取需要的特征列，返回pandas.DataFrame对象
y = np.array(my_iris["sepal_length"]) # 提取目标列,返回np.ndarray对象
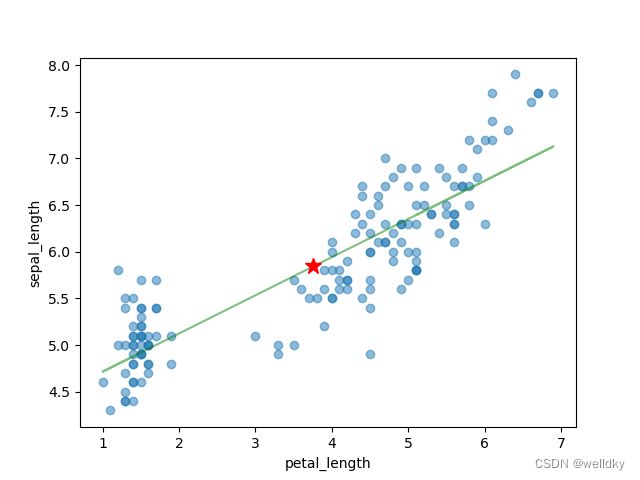
plt.plot(x, y, alpha = 0.5) # 绘制这些数据点

linreg = LinearRegression() # 创建一个线性回归模型实例
linreg.fit(x, y) # 模型训练
print("f(x) = ", linreg.intercept_, "+", linreg.coef_[0], "x") # 把回归系数和截距以公式的形式显示

pred_y = linreg.predict(x) # 模型预测
plt.plot(x, pred_y, 'g', alpha = 0.5) # 将预测曲线也画在图上
plt.plot(np.array(x).mean(), y.mean(), "r*", ms = 12) # 把回归直线必过的点用五角星强调
plt.gca().set_xlabel(feature_cols)
plt.gca().set_ylabel("sepal_length")
print("RMSE = ", np.sqrt(metrics.mean_squared_error(y, pred_y))) # 计算RMSE并输出

'''
	输出结果
	f(x) =  4.305565456292049 + 0.4091258984678836 x
	RMSE =  0.40435105064202476
'''

以上代码用到的方法
LinearRegression( )方法：创建一个线性回归模型的实例
模型实例.fit(x, y)方法：用于模型训练，x代表特征，y代表目标
模型实例.predict(x)方法：用于预测，x代表预测对象的特征
线性回归模型的intercept_属性：代表截距
线性回归模型的linreg.coef_[0]属性：代表回归系数
metrics.mean_squared_error( y_true, y_pred )方法：计算均方误差，y_true代表真实值，y_pred代表预测值，返回np.float64类型
np.sqrt( )方法：计算给定数组中每个元素的平方根

（2）线性回归模型性能评价标准

回归效果评价参数：决定系数$r^2$
$$r^2=\frac{S{S}_{regression}}{S{S}_{total}}=\frac{\sum _{k=1}^n(\widehat{y_k}-y_k{)}^2}{\sum _{k=1}^n(y_k-\bar{y}{)}^2}$$
其中$r^2\in [0,1]$，越接近1则模型性能越好

以下代码连接于上个代码之后：求模型的决定系数

print("r_square = ", linreg.score(x, y))

'''
	输出结果
	r_square =  0.7599553107783261
'''

以上代码用到的方法：
模型实例.score( )方法：返回模型的评价分数
在线性回归模型中评价分数就是决定系数

（3）线性回归与线性相关

线性回归中的决定系数就是线性相关系数的平方

以下代码连接于上个代码之后，用于验证线性回归与线性相关的关系：

print(my_iris[[feature_cols, "sepal_length"]].corr()) # 求两两特征的线性相关系数
r = np.array(my_iris[[feature_cols, "sepal_length"]].corr()[["sepal_length"]].iloc(0)[0]) # 完成提取后仍是np.ndarray对象
print("r = ", r)
print("square of r = ", r ** 2)

'''
	输出结果
	              petal_length  sepal_length
	petal_length      1.000000      0.871754
	sepal_length      0.871754      1.000000
	
	r =  [0.87175416]
	square of r =  [0.75995531]
'''

（4）逻辑回归模型

基于一个或多个量化特征/自变量直接预测某件事发生的概率，由于概率取值0~1，故采用Logistic函数（Logistic函数输出预测变量——某事发生概率）

逻辑回归的一些概念：
①Logistic函数：$f(x)=\frac{1}{1+e^{-t}}$
自变量$t\in (-\infty ,+\infty )$，值域$f\in (0,1)$
②几率Odds：某事件发生的概率与不发生的概率之比$Odds=\frac{p}{1-p}$
自变量$p\in [0,1]$，值域$Odds\in [0,+\infty )$
③几率的自然对数：$log\_Odds=ln\frac{p}{1-p}$
自变量$p\in [0,1]$，值域$Odds\in (-\infty ,+\infty )$

概率、几率、对数几率代码举例：

import numpy as np
import pandas as pd
from matplotlib import pyplot as plt

table = pd.DataFrame({'prob':[0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 0.99]})
table['odds'] = table['prob']  / (1 - table['prob'])
table['log-odds'] = np.log(table['odds'])
print(table)

plt.plot(table['prob'], table['prob'], 'g')
plt.plot(table['prob'], table['odds'], 'y')
plt.plot(table['prob'], table['log-odds'], 'm')
plt.plot(0.5, 0, 'dr', ms = 10)
plt.ylim([-6, 6])
plt.legend(['probability', 'Odds', 'log_odds', '(0.5, 0)'])
plt.show()

'''
	输出结果
	   prob       odds  log-odds
	0  0.10   0.111111 -2.197225
	1  0.20   0.250000 -1.386294
	2  0.30   0.428571 -0.847298
	3  0.40   0.666667 -0.405465
	4  0.50   1.000000  0.000000
	5  0.60   1.500000  0.405465
	6  0.70   2.333333  0.847298
	7  0.80   4.000000  1.386294
	8  0.90   9.000000  2.197225
	9  0.99  99.000000  4.595120
'''

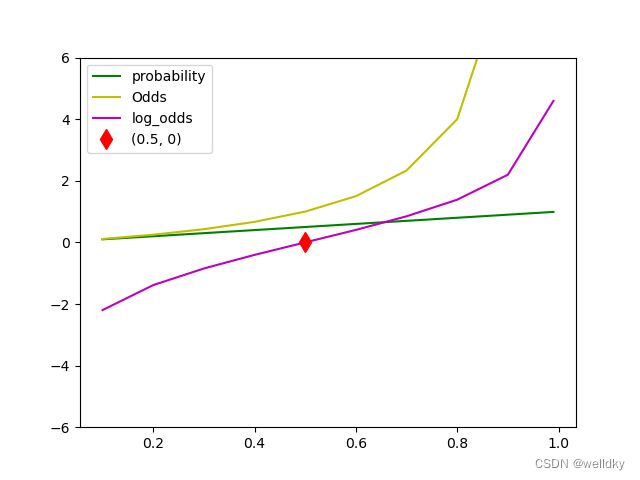
逻辑回归的实质：对对数几率作线性回归
$$ln\frac{p}{1-p}={\beta }_0+{\beta }_{1}x$$
二分类问题中，确定模型参数$\beta$不能应用线性回归的最小二乘法，而是最大化所有样本的对数似然函数

逻辑回归代码举例：

import numpy as np
import pandas as pd
from sklearn.linear_model import LogisticRegression # 逻辑回归需要导入的库
from sklearn.model_selection import train_test_split # 用于划分训练集、测试集
from matplotlib import pyplot as plt

bikes = pd.read_csv("bikeshare.csv") # 读取数据集
print(bikes.shape) # 输出数据集的基本信息

x = bikes[['temp']] # 将temp列作为特征（注意返回pandas.DataFrame对象）
y = bikes['count'] >= bikes['count'].mean() # 返回的是pandas.Series对象，内含索引号与一个布尔类型，代表是否数量大于平均值

# 划分训练集和测试集
x_train, x_test, y_train, y_test = train_test_split(x, y)

logreg = LogisticRegression() # 实例化一个模型对象
logreg.fit(x_train, y_train) # 拿训练集训练模型
print("分类的准确率为:", logreg.score(x_test, y_test)) # 利用测试集得到模型准确率
print(pd.DataFrame(np.transpose([y_test.values, logreg.predict(x_test)]), columns = {'真实值', '预测值'}).head()) # 将预测的测试集结果和实际的测试集结果组合拼接成一个二维数组，经过转置后再经过类型转换，生成pandas.DataFrame对象并返回前几行

'''
	输出结果
	分类的准确率为: 0.6697281410727406
       预测值 真实值
	0  False  False
	1   True  False
	2  False  False
	3  False   True
	4  False   True
	（原数组真实值在上，预测值在下；故而转置后预测值在前，真实值在后）
'''

以上代码用到的方法：
train_test_split(x, y, test_size = , random_state = )方法：用于随机划分训练集和测试集，通常用四个变量接收，分别代表：训练集特征、训练集目标、测试集特征、测试集目标
具体参数：
x 数据框 所有特征的集合
y 数组/序列 所有目标取值
test_size 浮点数/整数 训练集样本占比/训练集样本数量
random_state 随机数的种子

np.transpose( a )方法：调换数组的行列值的索引值（求转置）返回一个 np.ndarray 对象
具体参数：
a 数组 想要进行转置的数组

（5）训练集—测试集划分

模型使用的两个阶段：
阶段：模型建立fit(X, Y)$\to$模型应用predict(X)
任务：确定模型参数（在已有数据上最优）$\to$基于已有模型对新数据预测
数据：X已知，Y已知$\to$X已知，期待模型输出Y

数据足够多时，把文件分成两个集合：训练集与测试集，基于训练集进行建模，再对模型在测试集数据上的表现评分，最后用于预测

（6）非数值型特征作为输入时的 one-hot 编码

非数值型特征中的数字没有真实的数量意义
举例："季节"特征的1~4代表四个季节，但数字本身不含有数量意义

one-hot 编码：避免数字引入非真实数量意义，将类别型数据映射到一个始终只有一位置为"1"，其他位都是"0"的二进制编码，编码长度就是类别个数

以下代码连接于上个代码之后，是加入类别特征的逻辑回归举例：

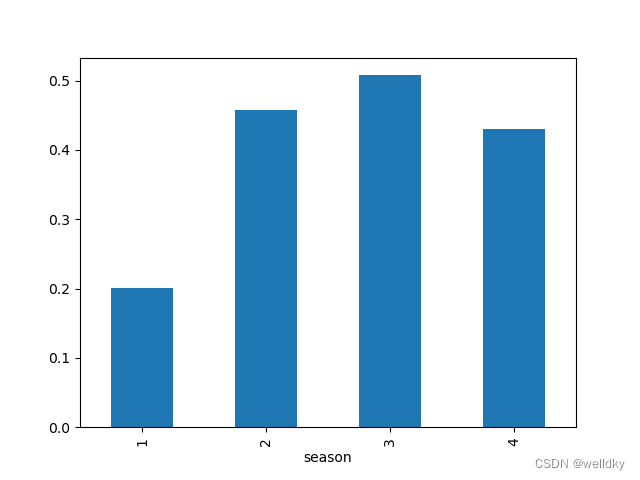
bikes['above_average'] = bikes['count'] >= bikes['count'].mean() # 返回的是pandas.Series对象，内含索引号与一个布尔类型，代表是否数量大于平均值，这里用数据集的新列去接受
bikes.groupby('season').above_average.mean().plot(kind = 'bar') # 统计各季节有多少大于平均数量（作出柱状图简单比较哪个季节数量较多）
plt.show()
when_dummies = pd.get_dummies(bikes['season'], prefix = 'season_') # 对季节采用one-hot编码
print(when_dummies.head()) # 展示出one-hot编码后的季节特征前几行

x = pd.concat([bikes[['temp']], when_dummies], axis = 1) # 将自行车数据的气温特征和one-hot编码列连接作为训练集
x_train, x_test, y_train, y_test = train_test_split(x, y)
logreg = LogisticRegression() # 实例化一个模型的对象
logreg.fit(x_train, y_train)
print("用气温、季节同时作为预测自变量,预测的准确率为:", logreg.score(x_test, y_test))

x = bikes[['temp', 'season']] #将自行车数据的气温特征和季节特征列连接作为训练集
x_train, x_test, y_train, y_test = train_test_split(x, y)
logreg = LogisticRegression() #实例化一个模型对象
logreg.fit(x_train, y_train)
print("用气温、季节同时作为预测自变量，但是不做季节特征的one-hot编码时,预测的准确率为:", logreg.score(x_test, y_test))

'''
	输出结果
		season__1  season__2  season__3  season__4
	 0          1          0          0          0
	 1          1          0          0          0
	 2          1          0          0          0
	 3          1          0          0          0
	 4          1          0          0          0
	用气温、季节同时作为预测自变量,预测的准确率为: 0.6914033798677444
	用气温、季节同时作为预测自变量,但是不做季节特征的one-hot编码时,预测的准确率为: 0.6337252020573108
'''

6.3 朴素贝叶斯模型

（1）贝叶斯定理

$$P(C|x)=\frac{P(x|C)P(C)}{P(x)}$$
其中，$x$代表观察变量，$C$代表潜在特征（比如分类的类别），$P(C)$代表先验概率，条件概率$P(C|x)$代表后验概率，条件概率$P(x|C)$代表似然性，$P(x)$代表归一化常数

补充①：全概率公式：$P(A)=\sum _{i=1}^{n}P(B_i)P(A/B_i)$
补充②：独立性：A、B相互独立，$P(AB)=P(A)P(B)$

举例：已知K疾病在某地区的发病率是0.1%，同时通过X检验来诊断K疾病的统计表如下，已知张三在一次X检验中呈阳性，求张三患K病和不患K病的概率各是多少。

是否患K病	X检验阳性	X检验阴性
患K病	99	1
不患K病	1	99

解：解题需利用全概率公式、贝叶斯定理
P(X_+)=P(X_+|患K病)P(患K病)+P(X_+|不患K病)P(不患K病)
p(患K病|X_+)=$\frac{P(X_{+}|患K病)P(患K病)}{P(X_{+})}$=9%
p(不患K病|X_+)=$\frac{P(X_{+}|不患K病)P(不患K病)}{P(X_{+})}$=91%
本例中的X检验不是好方法，性能不如空模型

以上为一个特征的贝叶斯模型，当推广至m个独立特征时，贝叶斯公式为：
$$P(C_k|X)=\frac{P(x_1|C_k)P(x_2|C_k)...P(x_m|C_k)}{P(X)}$$
即：
$$P(C_k|X)=\frac{P(C_k)\prod _{i=1}^{m}P(x_i|C_k)}{P(X)}$$
根据$P(x_i|C_k)$的不同情况，朴素贝叶斯模型则又可以分为：高斯模型、多项式模型、伯努利模型

（2）高斯模型

当特征$x$在每一类中都是服从高斯分布的连续值时构建的模型
sklearn库中的native_bayes模块有GaussianNB对象可以构建朴素贝叶斯的高斯模型

（3）多项式模型

当特征本身是离散值时构建的模型
sklearn库中的native_bayes模块有MultinomialNB对象可以构建朴素贝叶斯的多项式模型

（4）伯努利模型

当特征$x$是m个布尔值序列时构建的模型
sklearn库中的native_bayes模块有BernoulliNB对象可以构建朴素贝叶斯的伯努利模型

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import warnings
warnings.filterwarnings('ignore')
import  ssl
ssl._create_default_https_context = ssl._create_unverified_context

6.4 分类模型的性能评价指标

（1）混淆矩阵

二分类模型、多分类模型
将数据按待分的类别分组后，统计各组中模型分类或预测结果的矩阵

模型分类	真实分类
阳性	TP（真阳性）	FP（假阳性）
阴性	FN（假阴性）	TN（真阴性）

假阴性FN代表Ⅰ型错误，假阳性FP代表Ⅱ型错误

由混淆举证可以得到一些评价参数：
①准确率：$ACC=\frac{TP+TN}{Total}$
②真阳性率（召回率）：$TPR=\frac{TP}{TP+FN}$
③真阴性率：$TNR=\frac{TN}{TN+FP}$
④阳性预测值（精度）：$PPV=\frac{TP}{TP+FP}$
⑤阴性预测值：$NPV=\frac{TN}{TN+FN}$
⑥$F_1-score$：$F_1=\frac{2}{\frac{1}{TPR}+\frac{1}{PPV}}$，取值0~1，越靠近1代表性能越好
此类参数也可以推广至多分类，定义原理类似

（2）指标权衡

在模型的实际应用中，不能一味追求某个单一指标的最大化，而应该根据实际需求来权衡

（3）参数区分性能评价

线性二分类模型
通常采用ROC曲线（接收者操作特征曲线）下面积作为线性分类参数的性能评价：对同样的测试集，改变线性划分的阈值，随着阈值变化分类的TPR和FPR（即1-TNR）随之改变，以TPR为纵坐标，FPR为横坐标将选取不同阈值得到的给过以点画出连成曲线

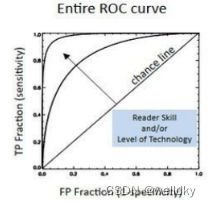
两个真实类别在预测特征上的分布重叠越少，参数分类性能越好，ROC曲线远离45°对角线；两个分布完全重叠时，两类别在该预测特征上完全不可分，ROC曲线退化为45°对角线
具体量化指标为ROC曲线下面积AUC，AUC取值0~1，越靠近1参数的线性区分性越好；越靠近0.5就越接近随机划分；小于0.5时分类倒置

ROC代码举例

import pandas as pd
import numpy as np
from sklearn import datasets
import matplotlib.pyplot as plt
from sklearn.metrics import roc_curve
from sklearn.metrics import roc_auc_score

# 从库中读取鸢尾花数据集
iris = datasets.load_iris()

my_auc = []
for n in range(4):
    my_auc.append(roc_auc_score(iris.target[:100], iris.data[:100, n])) # 分别对4个参数列求ROC_AUC，这边的切片分别取前100个目标值，和取每一个特征列的前100个值
print("4个参数的ROC_AUC是", my_auc)

# 将这些特征取值画在一张图上方便可视化观察
plt.plot(np.ones([50, 1]), iris.data[:50, 0], 'or') # 这50个点的横坐标是由np.ones()方法生成的，都是1，纵坐标是对应特征列的取值
plt.plot(np.ones([50, 1]) + 0.2, iris.data[50 : 100, 0], '*g') # 这50个点的横坐标是由np.ones()方法生成的，都是1.2(与上一列区分)，纵坐标是对应特征列的取值

plt.plot(np.ones([50, 1]) + 1, iris.data[:50, 0], 'or')
plt.plot(np.ones([50, 1]) + 1.2, iris.data[50 : 100, 1], '*g')

plt.plot(np.ones([50, 1]) + 2, iris.data[:50, 0], 'or')
plt.plot(np.ones([50, 1]) + 2.2, iris.data[50 : 100, 2], '*g')

plt.plot(np.ones([50, 1]) + 3, iris.data[:50, 0], 'or')
plt.plot(np.ones([50, 1]) + 3.2, iris.data[50 : 100, 3], '*g')

plt.xticks([1, 2, 3, 4], iris.feature_names)
plt.legend(iris.target_names[:2])

plt.show()

'''
	输出结果
	4个参数的ROC_AUC是 [0.9326, 0.07520000000000002, 1.0, 1.0]
'''

以上代码用到的方法：
sklearn库datasets的datasets.load_iris( )方法：用于获取集成在datasets内的鸢尾花数据集，该对象有两个属性，data和target分别代表特征列和目标，获取属性时返回的是np.ndarray对象
sklearn.metrics的roc_auc_score( )方法：用于获取AUC的结果，目标列在前（确保参数是 np.ndarray 类型）
plt.xticks( )方法：用于修改刻标
np.ones( shape )方法：返回给定形状和数据类型的数组，其中元素值为1
具体参数：
shape 数组 用于定义数组的大小

从图中可见，在petal length和petal width两项上，两种鸢尾花是可以完全区分的，故其ROC_AUC=1

（4）综合举例

综合举例：预分析鸢尾花数据

import pandas as pd
import numpy as np
from sklearn import datasets
from scipy import stats
import matplotlib.pyplot as plt
from os import environ
from sklearn.model_selection import train_test_split
from sklearn.naive_bayes import GaussianNB
from sklearn.metrics import confusion_matrix
from sklearn.metrics import classification_report

# 鸢尾花数据预分析
iris = datasets.load_iris() # 读取数据

plt.figure(figsize = (12, 15)) # 准备画布

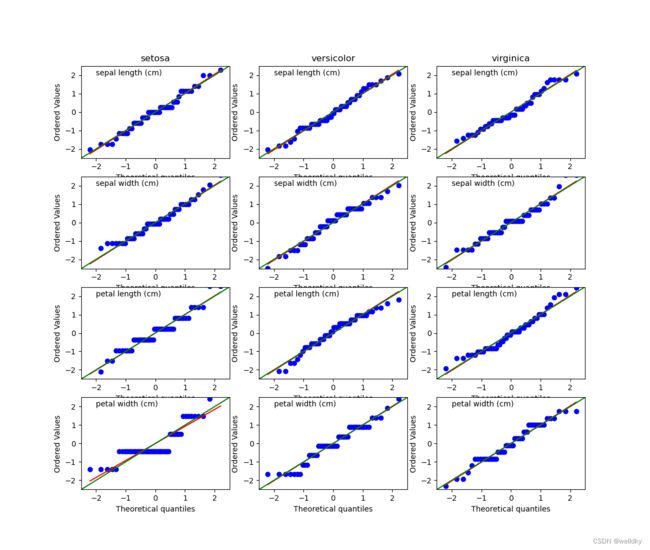
# 画图检验鸢尾花数据的特征是否服从高斯分布（这样才能判断用哪个朴素贝叶斯模型）
for n in range(4): # 外循环四次，代表了4个特征列
    for m in range(3): # 内循环三次，可见共有12张图
        x = (iris.data[m * 50 : m * 50 + 50, n]-iris.data[m * 50 : m * 50 + 50, n].mean()) / iris.data[m * 50 : m * 50 + 50, n].std() # m取值有0、1、2，这里的切片分别代表：第一个特征的每50个元素为一组，对组内每一个元素进行了标准化（使取值集中）
        plt.subplot(4, 3, n * 3 + m + 1) # 用于直接指定子图划分方式和位置进行绘图，这里4，3代表目前的大图有4行3列（12个小图），n*3+m+1代表当前画的子图的位置（取值1~12，依次标号）
        stats.probplot(x, dist = 'norm', plot = plt) # 计算数据的百分位点，并生成一幅以指定概率密度函数的百分位点为横坐标，数据实际百分位点为纵坐标的散点图，这里norm代表了高斯分布，选择plot=plt将所有的散点用最小二乘法拟合的直线画出（红色）

        plt.text(-2, 2, iris.feature_names[n]) # 在固定位置写下了文字说明（这里写下的是列特征名称）
        if n == 0: # 第一次外循环时
            plt.title(iris.target_names[m]) # 首行的标题名字设置为鸢尾花类别的名字
        else:
            plt.title('')
        
        plt.xlim([-2.5, 2.5]) # 限制x轴范围
        plt.ylim([-2.5, 2.5]) # 限制y轴范围
        plt.plot([-2.5, 2.5], [-2.5, 2.5], c = 'g') # 人为在每张图中画一条45°的线用来和拟合的直线作比较看看是否真的服从高斯分布
plt.show()

以上代码用到的方法：
plt.subplot( x, y, n )方法：用于直接指定子图划分方式和位置进行绘图，x，y分别代表大图的行数和列数，n代表当前画的子图的位置
plt.text( x, y, n)方法：用于在图片的(x, y)位置写下注释n
scipy库的stats.probplot( data, dist = , plot = )方法：计算数据的百分位点，并生成一幅以指定概率密度函数dist的百分位点为横坐标，数据实际百分位点为纵坐标的散点图，并用最小二乘法拟合直线，选择plot = plt则将图片画出
具体参数：
x 数组 数据集
dist 指定的概率密度函数，这里norm代表高斯分布
plot 决定是否将图片画出，这里plt代表画出

从图片上比较红色曲线（拟合的直线）与绿色曲线（标准的高斯分布直线）的重合情况，发现只有前两个特征拟合较好。
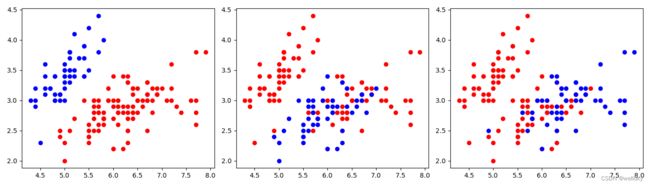
以这两个特征为参数去建立高斯-贝叶斯模型：

以下代码连接于上个代码之后：鸢尾花数据的高斯-贝叶斯模型建立：

# 鸢尾花高斯——贝叶斯模型构建
my_data = iris.data[:, :2] # 取前两列数据
X_train, X_test, Y_train, Y_test = train_test_split(my_data, iris.target, test_size = 0.2, random_state = 0)

clf = GaussianNB() # 实例化一个高斯-贝叶斯模型对象
clf.fit(X_train, Y_train) # 模型训练
Y_pred = clf.predict(X_test) # 模型预测

Y = pd.DataFrame(np.transpose([Y_test, Y_pred]), columns = {'true_type', 'predict_type'}) # 将预测结果和真实结果组成数组，转置，转换为pandas.DataFrame对象
print(Y.head(10)) # 展示前10条

'''
	输出结果
	   predict_type  true_type
	0             2          1
	1             1          1
	2             0          0
	3             2          2
	4             0          0
	5             2          2
	6             0          0
	7             1          2
	8             1          2
	9             1          1
'''

以下代码连接于上个代码之后：用于对建好的高斯-贝叶斯模型进行性能评价：

# 鸢尾花高斯——贝叶斯模型性能评价
print(confusion_matrix(Y_test, Y_pred)) # 生成一个三分类的混淆矩阵
print(classification_report(Y_test, Y_pred))

'''
	输出结果
	[[11  0  0]
	 [ 0  9  4]
	 [ 0  4  2]]
	     	      precision    recall  f1-score   support
	           0       1.00      1.00      1.00        11
	           1       0.69      0.69      0.69        13
	           2       0.33      0.33      0.33         6
	
	    accuracy                           0.73        30
	   macro avg       0.68      0.68      0.68        30
	weighted avg       0.73      0.73      0.73        30
'''

以上代码用到的方法：
sklearn.metrics的confusion_matrix( )方法：用于生成混淆矩阵
sklearn.metrics的classification_report( )方法：用于输出一些分类模型的指标，其中macro avg(宏平均)代表对应参数在所有类别上的平均值，weighted avg(加权平均)代表对应参数用类别的样本占比加权后的平均值

6.5 决策树

一种既能做回归，又能做分类的模型

（1）决策树工作原理

类似编程中的条件分枝结构，通过对两个特征的条件判断，最后达到各个目标的“叶子节点”，实现分类任务。

（2）建模过程

建模（训练）遵循如下流程：
①计算数据纯度
②选择一个候选划分，并计算划分后数据纯度
③对所有特征重复操作②
④选择使纯度增加最大的特征作为当前的节点，分别对分支计算数据纯度
⑤再对剩下的特征重复②开始的过程，直到达到停止标准

停止标准：
①达到了预先设定的最大树深度
②所有特征都已经遍历完
③分支下全部数据都属于同一类别

纯度：数据集中包含类别的单一程度，（越趋向单一，纯度越高）
纯度通常采用的衡量：基尼系数、信息熵

（3）基尼系数

假设数据集D可能包含K个类别，基尼系数定义为：
$$Gini(D)=1-\sum _{i=1}^K{P}_i^2$$
其中$P_i$代表第$i$类在数据集D中出现的概率，可以由D中第$i$类个体的个数除以D中个体总数计算。
数据集中数据越纯（越趋于更少类别），基尼系数越小
纯度最高时：基尼系数为0
纯度最低时：基尼系数为最大值$\frac{K-1}{K}$，二分类时即为$\frac{1}{2}$

举例：已知某历史贷款客户数据集中按贷款风险分类的两类客户例数在引入特征“有无支票账户”后的风险分类情况如下，求基尼系数

风险	无支票账户	有支票账户
高风险	8	2
低风险	2	13

$Gini(无支票)=1-(\frac{8}{10}{)}^2-(\frac{2}{10}{)}^2=0.32$
$Gini(有支票)=1-(\frac{2}{15}{)}^2-(\frac{13}{15}{)}^2=0.23$
$Gini(风险)=Gini(有支票)\frac{有}{无+有}+Gini(无支票)\frac{无}{无+有}=0.27$

（4）综合举例

决策树模型代码演示

import pandas as pd
import numpy as np
from scipy import stats
from matplotlib import pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier # 决策树
from sklearn import tree

my_data = pd.read_csv("german_credit_data_dataset.csv") # 读取数据
print(my_data.info()) # 显示基本信息
print("其中高风险例数为:", (my_data['customer_type']).sum() - 1000) # 这里巧妙利用了类别标签。高低标签分别用数字1、2表示，数据集一共有1000条数据，取所有标签之和减去1000即可得到高风险的例数

'''
	输出结果
	
	RangeIndex: 1000 entries, 0 to 999
	Data columns (total 21 columns):
	 #   Column                   Non-Null Count  Dtype  
	---  ------                   --------------  -----
	 0   checking_account_status  1000 non-null   object
	 1   duration                 1000 non-null   int64
	 2   credit_history           1000 non-null   object
	 3   purpose                  1000 non-null   object
	 4   credit_amount            1000 non-null   float64
	 5   savings                  1000 non-null   object
	 6   present_employment       1000 non-null   object
	 7   installment_rate         1000 non-null   float64
	 8   personal                 1000 non-null   object
	 9   other_debtors            1000 non-null   object
	 10  present_residence        1000 non-null   float64
	 11  property                 1000 non-null   object
	 12  age                      1000 non-null   float64
	 13  other_installment_plans  1000 non-null   object
	 14  housing                  1000 non-null   object
	 15  existing_credits         1000 non-null   float64
	 16  job                      1000 non-null   object
	 17  dependents               1000 non-null   int64
	 18  telephone                1000 non-null   object
	 19  foreign_worker           1000 non-null   object
	 20  customer_type            1000 non-null   int64
	dtypes: float64(5), int64(3), object(13)
	memory usage: 164.2+ KB
	None
	其中高风险例数为: 300
'''

以下代码连接于上个代码之后：

feature_col = ["checking_account_status", "personal"] # 选择想要选取的特征列，这里是选来进行one-hot编码的
X = my_data[['customer_type', 'credit_amount']] # 提取"customer_type"和"credit_amount"特征
for n, my_str in enumerate(feature_col):
    my_dummy = pd.get_dummies(my_data[[my_str]], prefix = my_str)
    X = pd.concat([X, my_dummy], axis = 1) # 进行one-hot编码并将结果连接到选中特征中

XX_feature = ['credit_amount', 'checking_account_status_A14', 'personal_A91', 'personal_A92', 'personal_A93', 'personal_A94'] # 从特征列中再次选取要进行提取的特征，这里可以看见只取了checking_account_status的最后一列one-hot编码
XX = X[XX_feature] # 提取
Y = X['customer_type'] # 提取目标值（注意是Series对象）
X_train, X_test, Y_train, Y_test = train_test_split(XX, Y, test_size = 0.2, random_state = 0) # 划分

my_tree = DecisionTreeClassifier(max_depth = 3) # 实例化一个决策树模型对象，设置最大深度为3
my_tree.fit(X_train, Y_train) # 训练
print("分类结果为:", my_tree.predict(X_test),'\n')
print("平均准确率为:", my_tree.score(X_test, Y_test))

'''
	输出结果
	分类结果为: [1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 1
	 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
	 1 1 1 1 1 1 1 1 1 1 1 1 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
	 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 1 1 1 1 2 2
	 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
	 1 1 1 1 1 1 2 1 1 1 1 1 1 1 1]
	
	平均准确率为: 0.71
'''

以下代码连接于上个代码之后：

print(pd.DataFrame({'feature':XX.columns, 'importance':my_tree.feature_importances_}))

'''
	输出结果
	                       feature  importance
	0                credit_amount    0.314532
	1  checking_account_status_A14    0.671787
	2                 personal_A91    0.013680
	3                 personal_A92    0.000000
	4                 personal_A93    0.000000
	5                 personal_A94    0.000000
'''

以上代码用到的方法：
决策树模型实例化对象的feature_importances_属性：用于获得建模用的各个特征在分类任务中的重要性

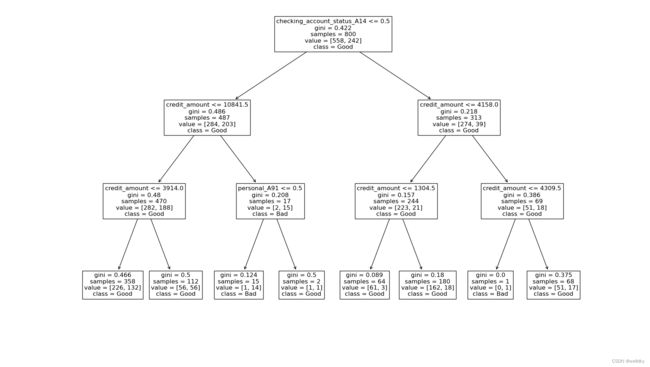
以下代码连接于上个代码之后，用于画出树状图展示：

plt.figure(figsize = (18, 12))
tree.plot_tree(my_tree, fontsize = 12, feature_names = XX.columns, class_names = ["Good", "Bad"])
plt.savefig("my_tree") # 保存为图片，可以添加路径
plt.show()

以上代码用到的方法：
sklearn库的tree.plot_tree( decision_tree, feature_names = , class_names = )方法：将训练好的树结构画出
具体参数：
decision_tree 训练好的决策树实例化对象
feature_names 列表 各特征的名字
class_names 列表 分类类别的名字
fontsize 整数 字体大小

6.6 有监督学习和无监督学习

有监督学习：从标签化训练数据集中推断出函数的机器学习任务
X被称为变量、特征、输入
Y被称为响应、目标、依赖变量、输出
无监督学习：根据类别未知的训练样本解决模式识别中的各种问题
TIP：PCA可以看作是一种无监督学习模型

6.7 K-means模型

实现聚类任务的无监督学习模型
K-means的相关概念：
Ⅰ簇：一组相似的数据
Ⅱ簇中心：簇中所有点的平均
Ⅲ数据空间：取n个特征构造出n维特征空间，每个数据都是空间中以其具体特征为坐标的点

（1）K-means迭代算法

建模（训练）遵循如下流程：
①选择K个初始的簇中心点
②遍历所有的点，把每个点分配到离它最近的簇
③重新计算簇中心点
④重复步骤②和③，直到达停止标准

停止标准：
①被重新分配类别的例数少于预设阈值
②簇中心点变化小于预测阈值
③迭代次数达到了预设阈值

K-means模型代码举例：

from turtle import color
import pandas as pd
import numpy as np
from scipy import stats
from matplotlib import projections, pyplot as plt
from sklearn.cluster import KMeans

my_data = pd.read_csv("tmdb_5000_movies.csv") # 读取数据
print(my_data.describe()) # 获取数值类数据的信息

'''
	输出结果
	             budget             id   popularity       revenue      runtime  vote_average    vote_count
	count  4.803000e+03    4803.000000  4803.000000  4.803000e+03  4801.000000   4803.000000   4803.000000
	mean   2.904504e+07   57165.484281    21.492301  8.226064e+07   106.875859      6.092172    690.217989
	std    4.072239e+07   88694.614033    31.816650  1.628571e+08    22.611935      1.194612   1234.585891
	min    0.000000e+00       5.000000     0.000000  0.000000e+00     0.000000      0.000000      0.000000
	25%    7.900000e+05    9014.500000     4.668070  0.000000e+00    94.000000      5.600000     54.000000
	50%    1.500000e+07   14629.000000    12.921594  1.917000e+07   103.000000      6.200000    235.000000
	75%    4.000000e+07   58610.500000    28.313505  9.291719e+07   118.000000      6.800000    737.000000
	max    3.800000e+08  459488.000000   875.581305  2.787965e+09   338.000000     10.000000  13752.000000
'''

以下代码连接于上个代码之后：

X = my_data[['budget', 'popularity', 'revenue']] # 提取需要的特征列
km = KMeans(n_clusters = 3, random_state = 1) # 实例化一个K-means模型的对象，其中n_clusters=3代表生成的聚类数为3
km.fit(X) # 训练
my_cl = pd.DataFrame(data = km.labels_, columns = ['cluster']) # 从训练结果中提取出得到的类别，转化为pd.DataFrame对象
X = pd.concat([X, my_cl], axis = 1) # 连接
print(X.head(5)) # 部分展示

'''
	输出结果
	      budget  popularity     revenue  cluster
	0  237000000  150.437577  2787965087        1
	1  300000000  139.082615   961000000        1
	2  245000000  107.376788   880674609        1
	3  250000000  112.312950  1084939099        1
	4  260000000   43.926995   284139100        2
'''

以上代码用到的方法：
KMeams模型对象的labels_属性：用于查看聚好的类别

以下代码连接于上个代码之后，用于查看每类数据特征平均值：

print(X.groupby('cluster').mean()) # 查看每类数据特征的平均值

'''
	输出结果
	               budget  popularity       revenue
	cluster
	0        1.721542e+07   14.292629  2.707764e+07
	1        1.496765e+08  110.824122  8.091626e+08
	2        7.318659e+07   45.302377  2.566544e+08
'''

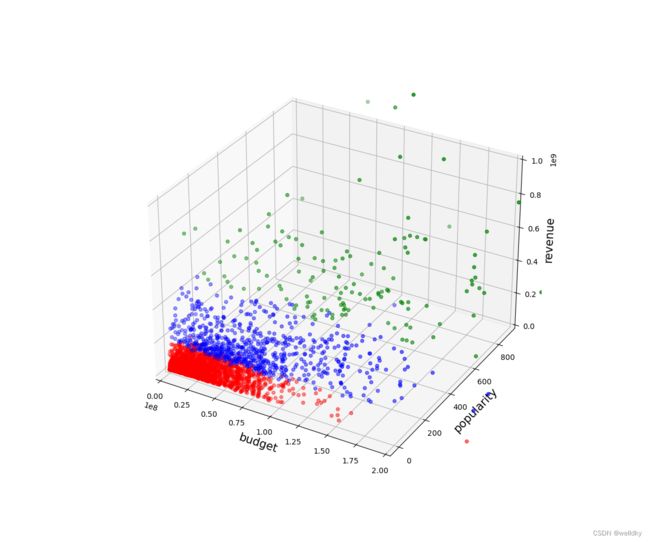
以下代码连接于上个代码之后，用于作图展示聚类：

x = X['budget']
y = X['popularity']
z = X['revenue']
colors = list()
palette = {0 : "red", 1 : "green", 2 : "blue"}
for n,row in enumerate(X['cluster']): # 为每一种分类标记不同颜色
    colors.append(palette[X['cluster'][n]])

fig = plt.figure(figsize = (12, 10))
ax = fig.gca(projection = '3d')
ax.scatter(x, y, z, color = colors)
ax.set_xlim(0, 2e8)
ax.set_zlim(0, 1e9)
ax.set_xlabel('budget', size = 15)
ax.set_ylabel('popularity', size = 15)
ax.set_zlabel('revenue', size = 15)
plt.show()

图中绿色点为受欢迎度和销量都很好的电影

6.8 偏差-方差权衡

（1）偏差-方差困境

相关概念回顾总结：
X：特征
y：响应测量值
$f$：y与X之间的真实关系
$\xi$：测量过程中的独立随机噪声（测量误差），不失一般性可以设为是均值$\mu =0$，标准差为$\sigma$的独立随机噪声
$\hat{y}=\hat{f}(x)$：实际建立的模型
$E[(y-\hat{f}{)}^2]$：衡量模型性能使用的平方误差

代入计算最终可得：
$E[(y-\hat{f}{)}^2]=(Bias(\hat{f}){)}^2+var(\hat{f})+{\sigma }^2$

每一项的定义：
偏差：$bia{s}^2=(f-E[\hat{f}]{)}^2$衡量模型准确性，越小越好
模型方差：$var(\hat{f})=E[(E[\hat{f}]-\hat{f}{)}^2]$衡量模型变异性、稳定性，越小越好
噪声方差：${\sigma }^2$

反应模型性能的平方误差，由偏差、模型方差、噪声方差共同决定
偏差-方差定义：偏差与方差存在此消彼长的矛盾

偏差-方差困境代码举例：

import pandas as pd
import numpy as np
from matplotlib import pyplot as plt
import seaborn as sns

# 读取数据
df = pd.read_csv("iris.csv", header = None, names = ['sepal_length', 'sepal_width', 'petal_length', 'petal_width', 'target'])
my_data = df[['sepal_length', 'sepal_width']].iloc[:50] # 这里取了鸢尾花数据的两个特征列的前50条数据
sns.lmplot(x = 'sepal_length', y = 'sepal_width', data = my_data, ci = None) # 利用这个方法可以做到在回归的同时把样本散点图和回归线画出
plt.show()

# 本例取的数据都是同一类别的鸢尾花，现在我们假设其不同类，并随机打上标签
my_data['sample'] = np.random.randint(1, 3, len(my_data))
print(my_data.head())

sns.lmplot(x = 'sepal_length', y = 'sepal_width', data = my_data, ci = None, hue = 'sample') # 再次做回归，这次是对这两类分别做的回归
plt.show()

sns.lmplot(x = 'sepal_length', y = 'sepal_width', data = my_data, ci = None, hue = 'sample', order = 6) # 再次做回归，但本次不做线性回归并设置回归阶数
plt.ylim(2.5, 4.5) # 限定y的取值范围
plt.show()

'''
	输出结果
	   sepal_length  sepal_width  sample
	0           5.1          3.5       2
	1           4.9          3.0       2
	2           4.7          3.2       2
	3           4.6          3.1       2
	4           5.0          3.6       2
'''

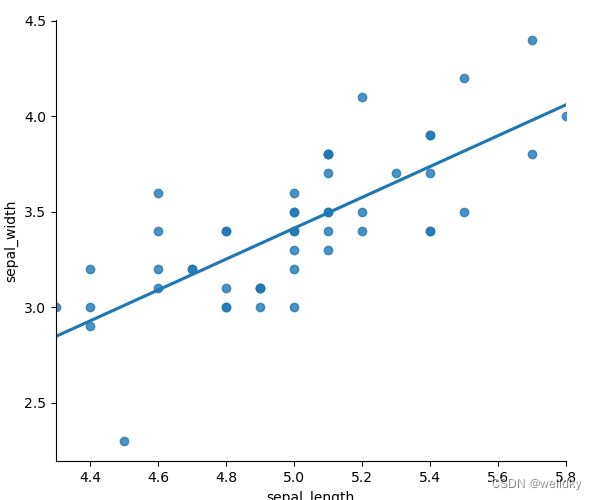
落在直线上的点很少：高偏差

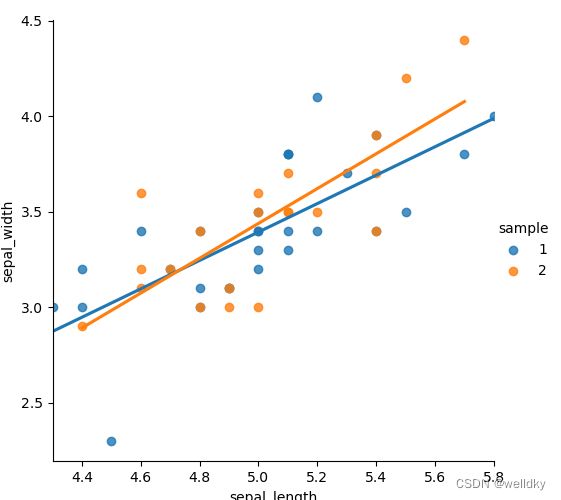
从第二张图可以看出，事实上数据都是来源于同一类别的，即使随机打上标签，最终拟合出的曲线也大致相似
两条拟合的直线非常接近：低方差
落在直线上的点很少：高偏差

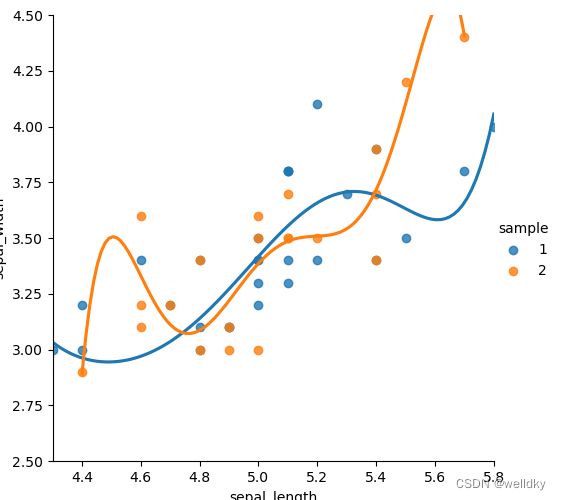
两条拟合的回归线变得迥异：方差变大
落在拟合回归线上的点变多：偏差变小

以上代码用到的方法：
seaborn 的 lmplot(x, y, data, ci = , hue = , order = ) 方法：用于绘制将散点图和拟合的回归线
具体参数：
x, y 字符串 所选数据的列名，同时也是坐标轴名称
data 数组 数据集
ci int [0，100]或None，表示回归估计的置信区间的大小
hue 数组 数据的定义子集，这里通常是标签
order int 大于1 表示回归的阶数

本例中，可以在代码的最前端加上声明%matplotlib inline，这样就可以省掉plt.show()的过程

（2）过拟合与欠拟合

偏差-方差困境带来的直接后果为过拟合和欠拟合
训练集偏差大：欠拟合Underfitting
此时需要增加特征或增加模型复杂度
训练集偏差小，测试集偏差大：过拟合Overfitting
此时需要减少特征、降低模型复杂度或扩大样本集合

偏差-方差权衡：一般而言，会存在一个最优点使两者达到折中，权衡便是寻找这个点

过拟合与欠拟合代码举例：

from sklearn.model_selection import train_test_split
import numpy as np
import pandas as pd
from matplotlib import pyplot as plt

# 定义一个方法，给定预测变量、真实响应、多项式参数，返回RMSE
def rmse(x, y, coefs):
    yfit = np.polyval(coefs, x) # 根据预测变量和多项式参数求出模型响应
    rmse = np.sqrt(np.mean((y - yfit) ** 2)) # 根据模型响应和真实响应的差别计算RMSE
    return rmse

# 读取数据
df = pd.read_csv("iris.csv", header = None, names = ['sepal_length', 'sepal_width', 'petal_length', 'petal_width', 'target'])
my_data = df[['sepal_length', 'sepal_width']].iloc[:50] # 依旧只取前两列特征的前50个数据

# 划分训练集与测试集
xtrain, xtest, ytrain, ytest = train_test_split(my_data['sepal_length'], my_data['sepal_width'], test_size = 0.5)

# 建立两个数组分别用来存放训练集的RMSE和测试集的RMSE
train_err = []
validation_err = []
degrees = range(1, 8) # 给定一个模型阶数的范围

for i,d in enumerate(degrees): # 这里的i是序号，从0开始循环；d是degrees范围内的模型阶数
    p = np.polyfit(xtrain, ytrain, d) # 通过训练集数据和给定阶数求得拟合系数
    train_err.append(rmse(xtrain, ytrain, p)) # 在这个拟合系数下求训练集RMSE
    validation_err.append(rmse(xtest, ytest, p)) # 在这个拟合系数下求测试集RMSE

fig, ax = plt.subplots() # 作图
ax.plot(degrees, validation_err, lw = 2, label = 'testing error') # 绘制曲线
ax.plot(degrees, train_err, lw = 2, label = 'training error')

ax.legend(loc = 0)
ax.set_xlabel('degree of polynomial')
ax.set_ylabel('RMSE')
plt.show()

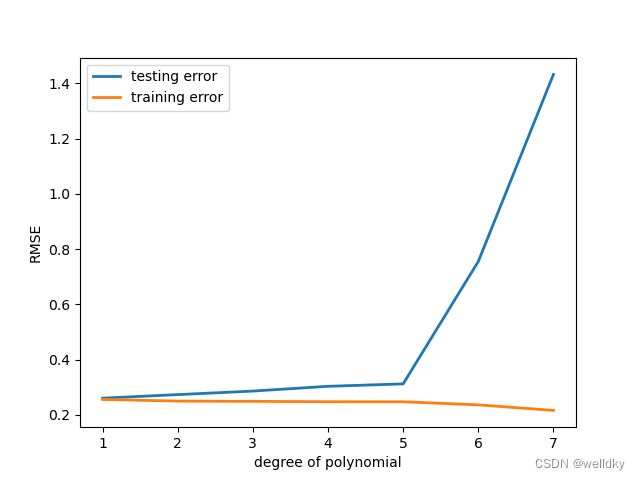
从图中可见，随着模型阶数上升，训练集RMSE趋于下降，而测试集RMSE趋于上升

以上代码用到的具体方法：
numpy 的 polyval(p, x) 方法：以特定值计算多项式，本例中是根据预测变量和多项式参数求出模型响应
具体参数：
p 数组 从最高次数到常数项的多项式系数的一维数组
x 数组 一个数字、一个数字数组，用于计算相应的值

numpy 的 polyfit(x, y, deg) 方法：最小二乘多项式拟合，本例中是通过训练集数据和给定阶数求得一组拟合系数
具体参数：
x 数组 特征数据
y 数组 标签数据
deg int 模型阶数（拟合多项式的次数）

plt 的 subplots() 方法：用来创建总画布/figure“窗口”，有figure就可以在其上作图

（3）K-折交叉验证

在偏差-方差困境中客观的评价模型使用的策略
K-折交叉验证的步骤：
①将已知真实响应的数据随机划分K等份
②采用其中一份做测试集，剩下K-1份做训练集，训练模型并在测试集评价模型的性能
③换一份做测试集，重复步骤②，直到所有的数据都当过测试集
④做完k次训练与测试，将k次的模型评价参数求平均来作为模型整体性能

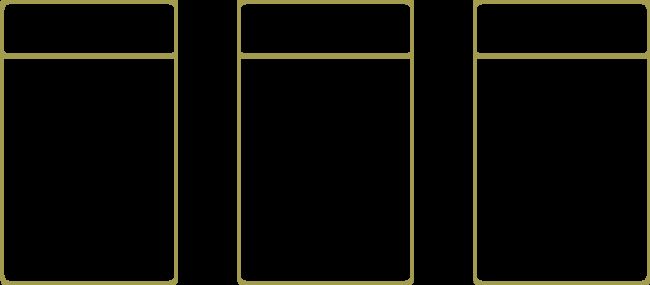
利用图像展示K折法的数据划分：

import pandas as pd
from matplotlib import pyplot as plt
from sklearn.model_selection import KFold

# 读取数据
df = pd.read_csv("iris.csv", header = None, names = ['sepal_length', 'sepal_width', 'petal_length', 'petal_width', 'target'])
my_data = df[['sepal_length', 'sepal_width']] # 取两个特征列

nfolds = 3 # 设置3折法
fig, axes = plt.subplots(1, nfolds, figsize = (14, 4)) # 作一个1行3列的大图
kf = KFold(n_splits = nfolds) # 把原始数据分割为K个子集，每次将其中一个子集作为测试集，其余K-1个子集作为训练集
i = 0

for training, validation in kf.split(my_data): # split方法会根据折数对数据划分，这里分别用training和validation两个变量来接收，接受的是index序列（遍历）
    x, y = my_data.iloc[training]['sepal_length'], df.iloc[training]['sepal_width'] # 不一定要用df，这里用my_data即可，本书作者可能有某种执念（悲）
    axes[i].plot(x, y, 'ro') # 在第i张子图上作画红色的散点表示划分出的训练集
    x, y = my_data.iloc[validation]['sepal_length'], df.iloc[validation]['sepal_width']
    axes[i].plot(x, y, 'bo') # 在第i张子图上作画蓝色的散点表示划分出的测试集
    i = i + 1
plt.tight_layout() # 自动调整子图参数，使之填充整个图像区域
plt.show()

以上代码用到的方法：
sklearn.model_selection 的 KFold(n_split, random_state, shuffle) 方法：用于k折法的数据划分（这是一个构造方法，构造了对象）
具体参数：
n_split int 需要划分的折数
random_state 随机数种子
shuffle 布尔型 是否打乱数据的顺序

KFold 对象的 split( ) 方法：返回分类后数据集的index
plt 的 tight_layout( ) 方法：自动调整子图参数，使之填充整个图像区域

K-折交叉验证法应用代码举例：

import pandas as pd
from sklearn.model_selection import cross_val_score
from sklearn.neighbors import KNeighborsClassifier

# 这里额外对数据集打了标签，读者也可以使用数据集原有的target特征列，把字符串改成数字即可
my_class = []
for n in range(150):
    if n < 50:
        my_class.append(1)
    elif n < 100:
        my_class.append(2)
    else:
        my_class.append(3)

# 读取数据
my_data = pd.read_csv("iris.csv", header = None, names = ['sepal_length', 'sepal_width', 'petal_length', 'petal_width', 'target'])

# 这里实例化了两个knn模型
knn1 = KNeighborsClassifier(n_neighbors = 1)
knn2 = KNeighborsClassifier(n_neighbors = 1)

# 第一次训练
knn1.fit(my_data[['sepal_length', 'sepal_width']], my_class)
print("训练集测试集相同时，模型的性能得分为:", knn1.score(my_data[['sepal_length', 'sepal_width']], my_class))

# 第二次训练
scores = cross_val_score(knn2, my_data[['sepal_length', 'sepal_width']], my_class, cv = 5, scoring = 'accuracy')
print("5折交叉验证时，模型的性能平均得分为:", scores.mean())

'''
	输出结果
	训练集测试集相同时，模型的性能得分为: 0.9266666666666666
	5折交叉验证时，模型的性能平均得分为: 0.7266666666666667	
'''

以上代码用到的方法：
sklearn.model_selection 的 cross_val_score (estimator, x, y, cv = , scoring =) 方法：实现特定模型的K折交叉验证
具体参数：
estimator 分类器/模型对象
x 数组 训练集
y 数组 测试集
cv int 需要划分的折数
scoring 字符串 评估学习器性能的标准，常用“Accuracy”等

需要注意：cross_val_score方法返回的是含有k个score的数组，后序可以利用mean( )方法或best_score_属性取值

6.9 参数的网格搜索

由于偏差-方差困境，必须协调考虑模型在训练集上的精确度与面对新数据时的泛化能力，这种协调考虑是一个调参的过程

常用的两种的调参方法：
①for循环+K-折交叉验证
②交叉验证网格搜索函数GridSearchCV

（1）for循环+K-折交叉验证

for循环+K-折交叉验证调参代码举例：

import pandas as pd
import numpy as np
from matplotlib import pyplot as plt
from sklearn.model_selection import cross_val_score, GridSearchCV
from sklearn.neighbors import KNeighborsClassifier

# 读取数据
df = pd.read_csv("iris.csv", header = None, names = ['sepal_length', 'sepal_width', 'petal_length', 'petal_width', 'target'])
my_data = df[['sepal_length', 'sepal_width']] # 提取两个特征列

# 这里额外对数据集打了标签，读者也可以使用数据集原有的target特征列，把字符串改成数字即可
my_class = []
for n in range(150):
    if n < 50:
        my_class.append(1)
    elif n < 100:
        my_class.append(2)
    else:
        my_class.append(3)

k_range = range(1, 30) # 为要调试的参数k设置范围
errors = [] # 创建列表用于存放准确率/错误率
for k in k_range:
    knn = KNeighborsClassifier(n_neighbors = k) # 用不同的k值作为参数实例化模型对象
    scores = cross_val_score(knn, df[['sepal_length', 'sepal_width']], my_class, cv = 5, scoring = 'accuracy') # 利用5折交叉验证法评估模型
    accuracy = np.mean(scores) # 得到准确率（对分数求平均）；用scores.mean()也完全可以
    error = 1 - accuracy # 得到错误率
    errors.append(error) # 存放

# 作图
plt.figure()
plt.plot(k_range, errors)
plt.xlabel('k')
plt.ylabel('error rates')
plt.show()  

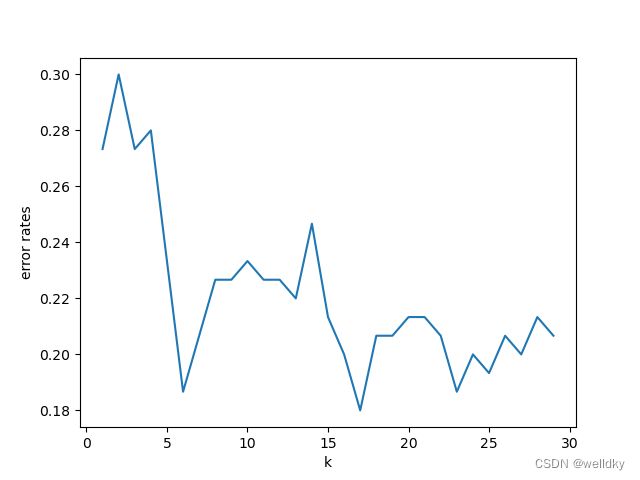
从图中可以看出随着k的增加，出错率一开始整体下降，到7以后又出现震荡

（2）交叉验证网格搜索函数GridSearchCV

思路：调用GridSearchCV方法生成实例化对象，调用fit方法对模型进行拟合检验，最后展示最佳性能的得分和对应的最优参数组合

以下代码连接于上个代码之后：
交叉验证网格搜索函数GridSearchCV调单个参数代码示例：

knn = KNeighborsClassifier() # 实例化一个knn模型对象
k_range = range(1, 30) # 给定k的范围
param_grid = dict(n_neighbors = k_range) # 将想要进行调参的参数放在一个字典中，这个字典一般命名为param_grid
grid = GridSearchCV(knn, param_grid, cv = 5, scoring = 'accuracy') # 调参
grid.fit(my_data[['sepal_length', 'sepal_width']], my_class)
print(pd.DataFrame(grid.cv_results_).head(5)) # 展示具体的调参情况

grid_mean_scores = grid.cv_results_['mean_test_score'] # 提取我们关心的特征列
print(grid_mean_scores, '\n')

# 作图
plt.figure()
plt.xlabel('Tuning Parameter: N nearest neighbors')
plt.ylabel('Classification Accuracy')
plt.plot(k_range, grid_mean_scores)

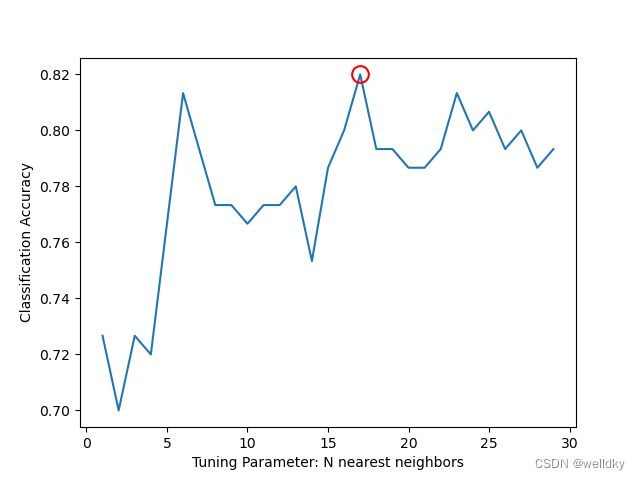
print("最高得分是邻近值取k = ", grid.best_params_['n_neighbors'], "时的得分", grid.best_score_)
plt.plot(grid.best_params_['n_neighbors'], grid.best_score_, 'ro', markersize = 12, markeredgewidth = 1.5, markerfacecolor = 'None', markeredgecolor = 'r') # 把取得最高评估的参数条件在图中标注展示
plt.show()

'''
	输出结果
	   mean_fit_time  std_fit_time  mean_score_time  std_score_time  ... split4_test_score mean_test_score  std_test_score  rank_test_score
	0       0.007355      0.001718         0.009315        0.002013  ...          0.666667        0.726667        0.061101               26
	1       0.004803      0.003921         0.010533        0.004736  ...          0.633333        0.700000        0.047140               29
	2       0.009503      0.005864         0.006476        0.006077  ...          0.666667        0.726667        0.090431               26
	3       0.004827      0.006441         0.011492        0.005808  ...          0.600000        0.720000        0.077746               28
	4       0.006485      0.005927         0.009230        0.007307  ...          0.766667        0.766667        0.055777               23

	[5 rows x 14 columns]
	[0.72666667 0.7        0.72666667 0.72       0.76666667 0.81333333
	 0.79333333 0.77333333 0.77333333 0.76666667 0.77333333 0.77333333
	 0.78       0.75333333 0.78666667 0.8        0.82       0.79333333
	 0.79333333 0.78666667 0.78666667 0.79333333 0.81333333 0.8
	 0.80666667 0.79333333 0.8        0.78666667 0.79333333]
	
	最高得分是邻近值取k =  17 时的得分 0.82
'''

以上代码用到的方法：
sklearn.model_selection 的 GridSearchCV(estimator, param_grid, cv = , scoring = ) 方法：用于自动调参，给出最优化结果和参数
具体参数：
estimator 分类器/模型对象
param_grid 字典 把想要调参的参数置于该字典
cv int 需要划分的折数
scoring 字符串 评估学习器性能的标准，常用“Accuracy”等

GridSearchCV 对象的 cv_results_ 属性：是数组，内含网格建模的具体情况
GridSearchCV 对象的 best_score_ 属性：是浮点数，best_estimator的最高分数
GridSearchCV 对象的 best_parmas_ 属性：是数组，内含最佳参数搭配

程序自动搜索得到的最佳参数是17，但结合图像，k=17已经处于震荡区，且对于每类50个样本容量的数据，17个邻近过多，故结合实际可取6

以下代码连接于上个代码之后：
交叉验证网格搜索函数GridSearchCV调多个参数代码示例：

knn = KNeighborsClassifier() # 实例化一个knn模型对象
k_range = range(1, 30) # 给定k值的取值范围
algorithm_opt = ['kd_tree', 'ball_tree'] # 给定algorithm_opt参数的取值范围
p_range = range(1, 5) # 给定p值的取值范围
weight_range = ['uniform', 'distance'] # 给定weight的取值范围
param_grid = dict(n_neighbors = k_range, weights = weight_range, algorithm = algorithm_opt, p = p_range) # 封装进同一个字典
'''
	此处还可以有如下的习惯写法：
	param_grid = {"k_range":range(1, 30),
				  "p_range":range(1, 5),
				  "algorithm_opt":['kd_tree', 'ball_tree'],
				  "weight_range":['uniform', 'distance']}
'''

print("The parameter dict is:", param_grid)

grid = GridSearchCV(knn, param_grid, cv = 5, scoring = 'accuracy')
grid.fit(my_data[['sepal_length', 'sepal_width']], my_class)

print('The best score is:', grid.best_score_)
print('The best parameter set is:', grid.best_estimator_)

'''
	输出结果
	The parameter dict is: {'n_neighbors': range(1, 30), 'weights': ['uniform', 'distance'], 'algorithm': ['kd_tree', 'ball_tree'], 'p': range(1, 5)}
	The best score is: 0.82
	The best parameter set is: KNeighborsClassifier(algorithm='kd_tree', n_neighbors=17)
'''

6.10 集成学习

集成学习指将多个模型进行组合，以期获得比任何一个单独的模型都更好的性能

（1）孔多塞陪审团定理

多数投票正确的概率比任何人（模型）都更高；当人数（模型数）变得足够大时，多数投票的准确率将接近100%
孔多塞陪审团定理成立的两个条件：
①做集成的模型之间必须相互独立，即一个模型的判断不能影响其他模型
②单个模型的性能必须大于随机模型，即好模型集成在一起才能得到更好的模型

可以利用计算机来对集成提升性能进行模拟

集成提升性能的仿真模拟：

import numpy as np
import pandas as pd
from matplotlib import pyplot as plt

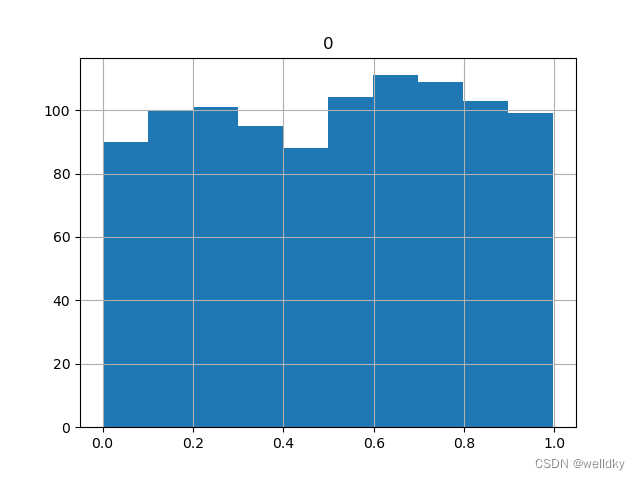
data1 = np.random.rand(1000) # 取1000个分布在[0, 1]之间的随机数
data2 = np.random.rand(1000)
data3 = np.random.rand(1000)
data4 = np.random.rand(1000)
data5 = np.random.rand(1000)

pd.DataFrame(data1).hist(bins = 10) # 做出直方图进行展示
plt.show()

print('data1的1000个数中,有', (data1 > 0.5).sum(), "个数据是大于0.5的")
print('data1的1000个数中,有', (data1 > 0.3).sum(), "个数据是大于0.3的")

model1 = np.where(data1 > 0.3, 1, 0) # 模拟：将大于0.3的都预测为1，否则预测为0
model2 = np.where(data2 > 0.3, 1, 0)
model3 = np.where(data3 > 0.3, 1, 0)
model4 = np.where(data4 > 0.3, 1, 0)
model5 = np.where(data5 > 0.3, 1, 0)
print("第一个模型的accuracy是:", model1.mean()) # 模拟：计算单个模型的准确率
print("第二个模型的accuracy是:", model2.mean())
print("第三个模型的accuracy是:", model3.mean())
print("第四个模型的accuracy是:", model4.mean())
print("第五个模型的accuracy是:", model5.mean())
ensemble_preds = np.round((model1 + model2 + model3 + model4 + model5) / 5.0).astype(int) # 将五个模型集成在一起，注意np.array之间的相加是对应位上的数据相加，然后取平均并转化为整数
print("集成模型的accuracy是:", ensemble_preds.mean()) # 得出集成后的准确率

'''
	输出结果
	data1的1000个数中,有 526 个数据是大于0.5的
	data1的1000个数中,有 709 个数据是大于0.3的
	第一个模型的accuracy是: 0.709
	第二个模型的accuracy是: 0.706
	第三个模型的accuracy是: 0.695
	第四个模型的accuracy是: 0.73
	第五个模型的accuracy是: 0.718
	集成模型的accuracy是: 0.849
'''

以上代码用到的方法：
numpy.round( )方法：对np.ndarray结构内的浮点数取整

本例中，如果一项数据有3个模型都判断为1，则最终会被判断为1

以下代码连接于上个代码之后：
集成不提升性能的仿真模拟：

model1 = np.where(data1 > 0.7, 1, 0)
model2 = np.where(data2 > 0.7, 1, 0)
model3 = np.where(data3 > 0.7, 1, 0)
model4 = np.where(data4 > 0.7, 1, 0)
model5 = np.where(data5 > 0.7, 1, 0)
print("第一个模型的accuracy是:", model1.mean())
print("第二个模型的accuracy是:", model2.mean())
print("第三个模型的accuracy是:", model3.mean())
print("第四个模型的accuracy是:", model4.mean())
print("第五个模型的accuracy是:", model5.mean())
ensemble_preds = np.round((model1 + model2 + model3 + model4 + model5) / 5.0).astype(int)
print("集成模型的accuracy是:", ensemble_preds.mean())


model1 = np.where(data1 > 0.7, 1, 0)
model2 = np.where(data2 > 0.3, 1, 0)
model3 = np.where(data3 > 0.6, 1, 0)
model4 = np.where(data4 > 0.2, 1, 0)
model5 = np.where(data5 > 0.5, 1, 0)
print("第一个模型的accuracy是:", model1.mean())
print("第二个模型的accuracy是:", model2.mean())
print("第三个模型的accuracy是:", model3.mean())
print("第四个模型的accuracy是:", model4.mean())
print("第五个模型的accuracy是:", model5.mean())
ensemble_preds = np.round((model1 + model2 + model3 + model4 + model5) / 5.0).astype(int)
print("集成模型的accuracy是:", ensemble_preds.mean())

'''
	输出结果
	第一个模型的accuracy是: 0.311
	第二个模型的accuracy是: 0.286
	第三个模型的accuracy是: 0.28
	第四个模型的accuracy是: 0.296
	第五个模型的accuracy是: 0.318
	集成模型的accuracy是: 0.147
	
	第一个模型的accuracy是: 0.311
	第二个模型的accuracy是: 0.706
	第三个模型的accuracy是: 0.366
	第四个模型的accuracy是: 0.805
	第五个模型的accuracy是: 0.516
	集成模型的accuracy是: 0.583
'''

（2）决策树集成

在实际应用中常将决策树进行集成
集成的两种方法：
①Bagging（bootstrap aggregation）：在原始的数据集上允许随机抽样，其训练步骤如下：
Ⅰ：对原始数据集做N次与原始样本容量相等的Bootstrap sample；
Ⅱ：基于这N个Bootstrap sample训练出N棵决策树；
Ⅲ：集成N棵决策树，若是分类任务，利用N棵决策树的结果进行投票决定集成输出；若是回归任务，对N棵决策树的结果求平均做出集成输出；
注意N需要足够大，决策树深度足够深，以保证低偏差
②随机森林：构建决策树时，从全体p个特征中随机挑选m个来进行bootstrap，这是与Bagging最大的区别，其训练步骤如下：
Ⅰ：对特征进行N次独立随机挑选作为单棵决策树的候选特征，对于回归任务，m取值[p/3, p]；对于分类任务，m取值$\sqrt{p}$；
Ⅱ：基于每个候选特征集合独立构建一棵回归树；
Ⅲ：N棵决策树的结果取平均或投票来形成输出；

随机森林代码示例：

import numpy as np
import pandas as pd
from matplotlib import pyplot as plt
from scipy import stats
from sklearn.tree import DecisionTreeClassifier
from sklearn.model_selection import cross_val_score
from sklearn.ensemble import RandomForestClassifier

my_data = pd.read_csv("german_credit_data_dataset.csv") # 读取数据
high_risk = my_data[['customer_type']] - 1 # 由于标签由1，2表示，全部-1后求和就可以直接快速得到高风险用户的人数
print('The number of high risk is:', high_risk.sum()) # 展示有多少高风险用户

feature_col = my_data.columns # 取所有特征列
X = my_data[['duration']] # 一个数值型特征
for n,my_str in enumerate(feature_col): # 遍历其他所有的特征
    if (my_str != 'customer_type') & (my_str != 'duration'): # 首先排除掉标签特征和选定的特征
    	if my_data[[my_str]].dtypes[0] != object: # 判断是否是数值型数据
        	X = pd.concat([X, my_data[[my_str]]], axis = 1) # 如果是数值型就直接附加上

for n,my_str in enumerate(feature_col): # 遍历其他所有的特征
	if my_data[[my_str]].dtypes[0] == object: # 判断是否是类别型数据
        my_dummy = pd.get_dummies(my_data[[my_str]], prefix = my_str) # 如果是类别型的数据就进行one-hot编码
        X = pd.concat([X, my_dummy], axis = 1) # 附加上

estimator_range = range(10, 400, 10) # 给定一个参数范围
my_scores = [] # 用于存储结果

for estimator in estimator_range:
    my_tree = RandomForestClassifier(n_estimators = estimator) # 实例化模型
    accuracy_scores = cross_val_score(my_tree, X, my_data['customer_type'], cv = 5, scoring = 'roc_auc') # 计算5折法得分，这里采用ROC曲线下面积作为评价标准
    my_scores.append(accuracy_scores.mean())

plt.plot(estimator_range, my_scores) # 将结果做图展示
plt.xlabel('the number of trees')
plt.ylabel('ROC_AUC')
plt.show()

my_RF = RandomForestClassifier(n_estimators = 150) # 取性能比较好的参数
my_RF.fit(X, my_data['customer_type']) # 训练模型
print(pd.DataFrame({'feature' : X.columns, 'importance' : my_RF.feature_importances_}).sort_values('importance', ascending = False)) # 比较各特征在分类中的重要性

'''
	输出结果
	The number of high risk is: customer_type    300
	dtype: int64
	                        feature  importance
	20                credit_amount    0.098536
	44                          age    0.081201
	0                      duration    0.077997
	4   checking_account_status_A14    0.049751
	1   checking_account_status_A11    0.040791
	..                          ...         ...
	59          foreign_worker_A201    0.003058
	52                     job_A171    0.002779
	12                 purpose_A410    0.001989
	15                  purpose_A44    0.001889
	18                  purpose_A48    0.001026
	
	[61 rows x 2 columns]
'''

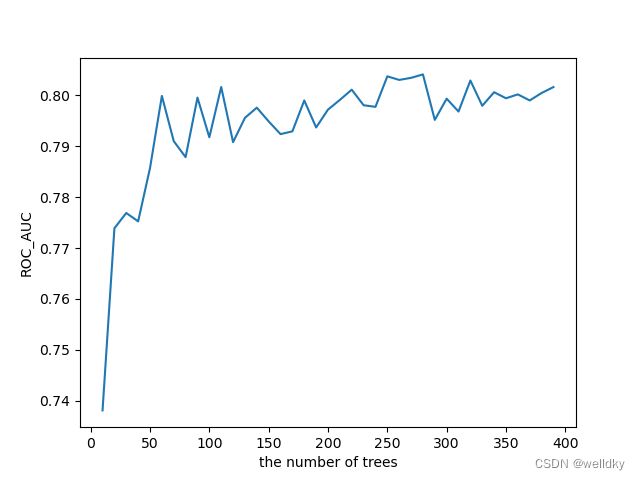
随机森林的优势：
1.性能较好
2.不必须交叉验证，其性能评价也较为可靠
3.特征的重要性排序可靠
随机森林的不足：
1.并行结构，训练和预测起来都比较慢
2.难以可视化

6.11 小结

本章节介绍了各种机器学习模型去完成各类不同的任务，以及各类模型的选择和评价：

当然教材内容自然是有限的，本博客作为笔记整理也是有限的。机器学习是特别庞大的邻域，这里希望能激发您进一步探究学习的欲望。

---

第七章 结果展示

7.1 区分面向对象的结果展示

7.2 展示过程中的可视化

可视化展示的两个层面：科学层面和人的层面
科学层面：准确、无歧义、禁止扭曲与误导、数据范围、量纲、线性坐标
人的层面：遵重人的逻辑习惯与主观感受
可视化展示的三个原则：方法由信息决定、自明性、合理信息容量与分辨率
可视化具体方法由传递的信息决定：

可视化要具备自明性，包含图本身和图中注解
合理选择一幅图中的信息容量和信息分辨率

---

小结

笔记的第三部分包含了数据科学项目处理流程中建模与性能评价和结果展示的相关理论内容与代码实例。本节内容理论结合实践，内容较为丰富，同样学习该门学科的读者不光需要结合教材熟练掌握理论知识，更应该亲自上手联系代码书写。至此教材的全部内容笔记梳理完毕。