语音处理/语音识别基础(五)- 声音的音量,过零率,音高的计算
如前面第3篇讲到,声音的几个主要特征有音量 Volume, 音高 Pitch, 音色 Timbre。
另外有一个重要的特征是过零率 zero crossing rate。
当我们在分析声音时,通常以「短时距分析」(Short-term Analysis)为主,因为音讯在短时间内是相对稳定的。我们通常将声音先切成帧(Frame),每一帧长度大约在 20 ms 左右,再根据帧内的信号来进行分析。
计算音量(Volume/Intensity/Energe)
「音量」代表声音的强度,又称为「响度」、「强度」(Intensity)或「能量」(Energy),可由一个音框内的讯号震幅大小来类比,基本上两种方式来计算:
1).每一个音帧的绝对值(信号绝对值)的总和: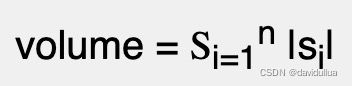
其中 si 是一个音帧中的第 i 个取样点,而 n 则是每个音帧包含的采样点数。这种方法的计算较简单,只需要整数运算,适合用于低端平台(如微电脑等)。
2).每一个音帧的信号值平方值的总和,再取以 10 为底对数值,再乘以10: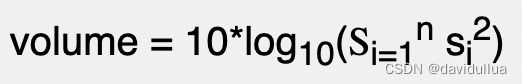
这种方法得到的值是以分贝(Decibels)为单位,是一个相对强度的值,比较符合人耳对于大小声音的感觉。以下网页有对分贝的详细说明:
dB: What is a decibel?
音量具有下列特性:
1.一般而言,有浊音(voiced sound)的音量大于清音/气音(unvoiced sound)的音量,而清音的音量又大于噪音的音量。
2.音量是一个相对性的指标,受到麦克风设定的影响很大。
3.通常用在端点侦测,估测浊音(Voiced sound)的音母或韵母的开始位置及结束位置。
4.在计算前最好先减去音讯讯号的平均值,以避免讯号的直流偏移(DC Bias)所导致的误差。 对于绝对值加和的方法,通常减去中位数( median subtraction )来计算; 而对于平方和取对数计算分贝的方法,通常减去平均数(mean substraction)来计算(目的都是为了使得一帧的总音量值在减去噪音的影响后尽可能小)。
上面是通过常量(固定的直流偏移/DC Bias 来做音量计算的零调整。
也可以通过多项式拟合的方法来找到直流偏移/噪音的曲线来做零调整。
在语音录制过程中,由于多种原因,包括静态效应、麦克风上的呼吸和 50Hz 交流电压信号,录制的语音信号很可能会在非零时变值附近振荡(偏移)。 为了避免在一帧内出现这种漂移,一种简单的方法是通过多项式拟合来识别时变零曲线(就是说即使没有声音的情况下, 也有在0点附近的信号时变近0信号),并通过在原始帧的曲线中删除噪音子轨道来消除漂移。
以下显示如何以两种方法(绝对值/分贝值,同时做零调整)来计算音量:
waveFile='sunday.wav';
% 帧大小取 256, 即每一帧 256 个采样点,两帧之间设置 123 个采样点的重叠。
frameSize=256;
overlap=128;
au=myAudioRead(waveFile); y=au.signal; fs=au.fs;
fprintf('Length of %s is %g sec.\n', waveFile, length(y)/fs);
% 调用 enframe 自动分帧
frameMat=enframe(y, frameSize, overlap);
frameNum=size(frameMat, 2);
% Compute volume using method 1
volume1=zeros(frameNum, 1);
for i=1:frameNum
frame=frameMat(:,i);
frame=frame-median(frame); % zero-justified
volume1(i)=sum(abs(frame)); % method 1
end
% Compute volume using method 2
volume2=zeros(frameNum, 1);
for i=1:frameNum
frame=frameMat(:,i);
frame=frame-mean(frame); % zero-justified
volume2(i)=10*log10(sum(frame.^2)+realmin); % method 2
end
sampleTime=(1:length(y))/fs;
frameTime=((0:frameNum-1)*(frameSize-overlap)+0.5*frameSize)/fs;
subplot(3,1,1); plot(sampleTime, y); ylabel(waveFile);
subplot(3,1,2); plot(frameTime, volume1, '.-'); ylabel('Volume (Abs. sum)');
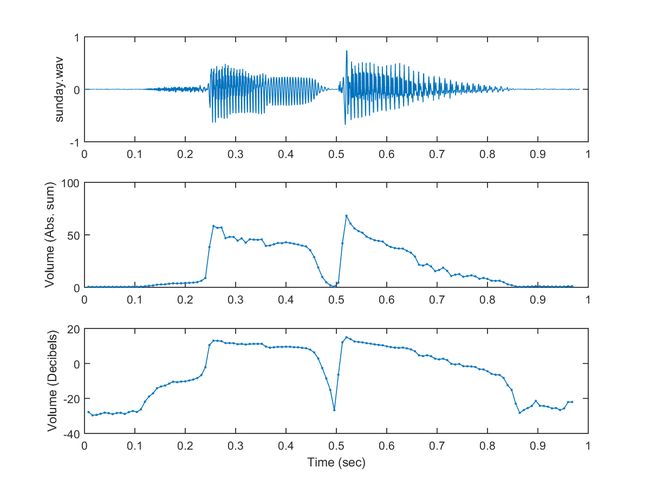
subplot(3,1,3); plot(frameTime, volume2, '.-'); ylabel('Volume (Decibels)'); xlabel('Time (sec)');分析绝对的音量,以及分贝值,得到这样的随着时间变化的波形图:
过零率(Zero Crossing Rate)的计算
「过零率」(Zero Crossing Rate,简称 ZCR)是在声音信号的每一帧中,声音信号的采样值通过零点的次数,具有下列特性:
1.一般而言,噪音及清音(unvoiced sound)的过零率均大于浊音(voiced sound)具有清晰可辨之音高,例如母音)。
2.ZCR 是噪音和清音(unvoiced sound)两者较难从过零率来分辨,会依照录音情况及环境噪音而互有高低。但通常清音的音量会大于噪音。
3.通常用在端点侦测,特别是用在估测清音的起始位置及结束位置。
4.可用来预估讯号的基频,但很容易出错,所以必须先进行前处理。
为了避免直流偏移,通常需要在每一帧里面减去均值。 直接计算过零率如下。
% zerocrossingrate.m
waveFile='csNthu.wav';
frameSize=256;
overlap=0;
au=myAudioRead(waveFile); y=au.signal; fs=au.fs;
frameMat=enframe(y, frameSize, overlap);
frameNum=size(frameMat, 2);
for i=1:frameNum
frameMat(:,i)=frameMat(:,i)-mean(frameMat(:,i)); % mean justification
end
zcr=sum(frameMat(1:end-1, :).*frameMat(2:end, :)<0);
sampleTime=(1:length(y))/fs;
frameTime=((0:frameNum-1)*(frameSize-overlap)+0.5*frameSize)/fs;
subplot(2,1,1); plot(sampleTime, y); ylabel('Amplitude'); title(waveFile);
subplot(2,1,2); plot(frameTime, zcr, '.-');
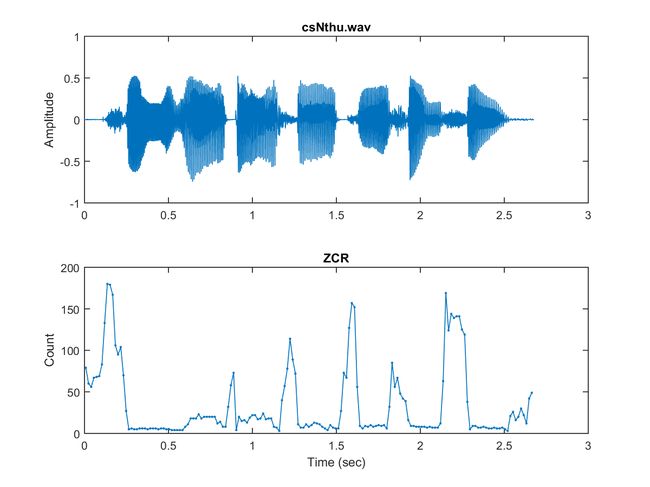
xlabel('Time (sec)'); ylabel('Count'); title('ZCR');可视化之后看到每个时刻点的信号量(归一后的信号量)、过零率的图
可以使用 frame2zcr 函数简化上面的例子,函数的 代码参考:
http://mirlab.org/jang/books/audiosignalprocessing/example.rar
waveFile='csNthu.wav';
frameSize=256;
overlap=0;
au=myAudioRead(waveFile); y=au.signal; fs=au.fs;
frameMat=enframe(y, frameSize, overlap);
frameNum=size(frameMat, 2);
zcr=frame2zcr(frameMat);
sampleTime=(1:length(y))/fs;
frameTime=frame2sampleIndex(1:frameNum, frameSize, overlap)/fs;
subplot(2,1,1); plot(sampleTime, y); ylabel('Amplitude'); title(waveFile);
subplot(2,1,2); plot(frameTime, zcr, '.-');
xlabel('Time (sec)'); ylabel('Count'); title('ZCR');为了使用过零率 ZCR 来区分清音(unvoiced sound)和环境噪音,我们在计算 ZCR 之前做一个波形的偏移,这个方法在噪音比较小的时候特别有用(即每一个信号都减去噪音信号值,假设最小声音的信号是噪音)
偏移量:取音量最小的帧中,最大采样值的绝对值的2倍。比如两种方法计算过滤率:
waveFile='csNthu.wav';
frameSize=256;
overlap=0;
au=myAudioRead(waveFile); y=au.signal; fs=au.fs;
frameMat=enframe(y, frameSize, overlap);
frameNum=size(frameMat,2);
volume=frame2volume(frameMat);
[minVolume, index]=min(volume);
% shiftAmount is equal to twice the max. abs. sample value within the frame of min. volume
shiftAmount=2*max(abs(frameMat(:,index)));
method=1;
zcr1=frame2zcr(frameMat, method);
zcr2=frame2zcr(frameMat, method, shiftAmount); % ZCR with shift
sampleTime=(1:length(y))/fs;
frameTime=frame2sampleIndex(1:frameNum, frameSize, overlap)/fs;
subplot(2,1,1); plot(sampleTime, y); ylabel('Amplitude'); title(waveFile);
subplot(2,1,2); plot(frameTime, zcr1, '.-', frameTime, zcr2, '.-');
xlabel('Time (sec)'); ylabel('Count'); title('ZCR');
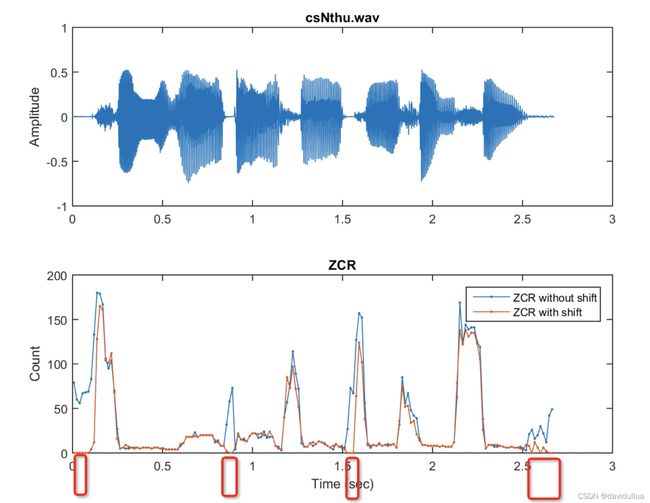
legend('ZCR without shift', 'ZCR with shift');得到如下的图,图中红色的为加上偏移之后的过零率,很明显加偏移后,纯噪音的过零率都变成0了。从而和清音区分开来。(清音、噪音的过零率较大,而加偏移后,噪音的过零率变成0)
在这个例子中,偏移等于最小音量帧内最大信号值绝对值的两倍。 因此,静音的 ZCR 大幅降低,这时使用 ZCR 更容易区分清音和静音。
此外,我们应该注意到以下情况:
1).如果一个样本恰好位于零处,我们是否应该将其视为过零? 根据对这个问题的回答,我们有两种实现 ZCR 的方法。
2).大多数 ZCR 计算基于音频信号的整数值。 如果我们想做均值减法,平均值也应该四舍五入到最接近的整数。
若要侦测声音的开始和结束,通常称为「端点侦测」(Endpoint Detection)或「语音侦测」(Speech Detection),最简单的方法就是使用音量和过零率来判别,相关内容后面再做分享。
音高的计算(Matlab 例子)
「音高」(Pitch)是另一个音讯里面很重要的特征,直觉地说,音高代表声音频率的高低,而此频率指的是「基本频率」(Fundamental Frequency),也就是「基本周期」(Fundamental Period)的倒数。这个频率跟采样率(Sample Rate, Frequency of Sampling)不是同一个概念。
音高的计算公式: pitch=69+12*log2(ff/440); 其中 ff 是基本频率。
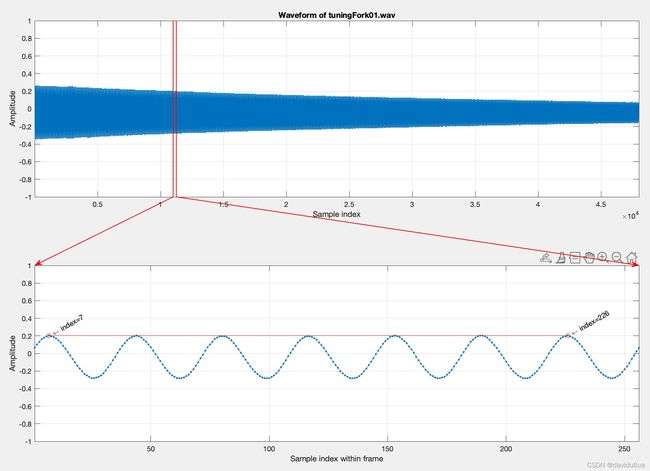
若直接观察音讯的波形,只要声音稳定,我们并不难直接看到基本周期的存在,以一个 3 秒的音叉声音来说,我们可以取一个 256 点的帧,将此帧画出来后,就可以很明显地看到基本周期,请见下列范例,对一个音叉发出来的声音做分析,计算:
waveFile='tuningFork01.wav';
au=myAudioRead(waveFile); y=au.signal; fs=au.fs;
index1=11000;
frameSize=256;
index2=index1+frameSize-1;
frame=y(index1:index2);
subplot(2,1,1); plot(y); grid on
xlabel('Sample index'); ylabel('Amplitude'); title(['Waveform of ', waveFile]);
axis([1, length(y), -1 1]);
subplot(2,1,2); plot(frame, '.-'); grid on
xlabel('Sample index within frame'); ylabel('Amplitude');
point=[7, 226]; % Peaks
axis([1, length(frame), -1 1]);
periodCount=6;
fp=((point(2)-point(1))/periodCount); % fundamental period
ff=fs/fp; % fundamental frequency
pitch=69+12*log2(ff/440);
fprintf('Fundamental period (fp) = (%g-%g)/%g = %g points\n', point(2), point(1), periodCount, fp);
fprintf('Fundamental frequency (ff) = %g/%g = %g Hz\n', fs, fp, ff);
fprintf('Pitch = %g semitone\n', pitch);
% === For plotting arrows, etc
% ====== Frame boundary
subplot(211);
line(index1*[1 1], [-1 1], 'color', 'r', 'linewidth', 1);
line(index2*[1 1], [-1 1], 'color', 'r', 'linewidth', 1);
% ====== FP coverage
subplot(212);
line(point, frame(point), 'marker', 'o', 'color', 'red');
% ====== Axis locations
subplot(211); loc1=get(gca, 'position');
subplot(212); loc2=get(gca, 'position');
% ====== arrow 1
x1=[loc1(1)+(index1(1)-1)/(length(y)-1)*loc1(3), loc2(1)];
y1=[loc1(2), loc2(2)+loc2(4)];
ah=annotation('arrow', x1, y1, 'color', 'r', 'linewidth', 1);
% ======= arrow 2
x2=[loc1(1)+(index2-1)/(length(y)-1)*loc1(3), loc2(1)+loc2(3)];
y2=[loc1(2), loc2(2)+loc2(4)];
ah=annotation('arrow', x2, y2, 'color', 'r', 'linewidth', 1);
% ====== Texts indicating start/end indices
h1=text(point(1), frame(point(1)), [' \leftarrow index=', int2str(point(1))], 'rotation', 30);
h2=text(point(2), frame(point(2)), [' \leftarrow index=', int2str(point(2))], 'rotation', 30);Fundamental period (fp) = (226-7)/6 = 36.5
points Fundamental frequency (ff) = 16000/36.5 = 438.356 Hz
Pitch = 68.9352 semitone
这个图示一个256个采样点的一帧音频的图。 从这个图中可以看出来,在一个简短的时间周期内,这个音频的信号是完全标准的周期性信号。
在上面的例子中,上图红线的位置代表音频这一帧的位置,下图即是 256 个采样点的帧,其中红线部分包含了 5 个基本周期,总共占掉了 182 单位点,因此对应的基本频率是 fs/(182/5) = 16000/(182/5) = 439.56 Hz,相当于 68.9827 半音(Semitone),其中由基本频率至半音的转换公式如下:
semitone = 69 + 12*log2(frequency/440)
换句话说,当基本频率是 440 Hz 时,对应到的半音差是 69,这就是钢琴的「中央 La」或是「A4」
一般音叉的震动频率非常接近 440 Hz,因此我们常用音叉来校正钢琴的音准。
上述公式所转换出来的半音音程,也是 MIDI 音乐档案所用的标准。从上述公式也可以看出:
1.每个全音阶包含 12 个半音(七个白键和五个黑键)。
2.每向上相隔一个全音阶,频率会变成两倍。例如,中央 la 是 440 Hz(69 Semitones),向上平移一个全音阶之后,频率就变成 880 Hz(81 Semitones)。
3.人耳对音高的「线性感觉」是随着基本频率的对数值成正比。
4.音叉的声音非常干净,整个波形非常接近弦波,所以基本周期显而易见。
在观察音讯波形时,每一个基本周期的开始点,我们称为「音高基准点」(Pitch Marks,简称 PM),PM 大部分是波形的局部最大点或最小点,例如在上述音叉的范例中,我们抓取的两个 PM 是局部最大点,而在我的声音的范例中,由于 PM 在局部最大点并不明显,因此我们抓取了两个局部最小点的 PM 来计算音高。 PM 通常用来调节一段声音的音高,在语音合成方面很重要。
由于生理构造不同,男女生的音高范围并不相同,一般而言:
男生的音高范围约在 35 ~ 72 半音,对应的频率是 62 ~ 523 Hz。
女生的音高范围约在 45 ~ 83 半音,对应的频率是 110 ~ 1000 Hz。
但是我们分辨男女的声并不是只凭音高,而还是依照音色(共振峰)。
使用「观察法」来算出音高,并不是太难的事,但是若要电脑自动算出音高,就需要更深入的研究。
音色
「音色」(Timber)是一个很模糊的名词,泛指音讯的内容,例如「天书」这两个字的发音,虽然都是第一声,因此它们的音高应该是蛮接近的,但是由于音色的不同,我们可以分辨这两个音。直觉来看,音色的不同,代表基本周期的波形不同,因此我们可以使用基本周期的波形来代表音色。若要从基本周期的波形来直接分析音色,是一件很困难的事。
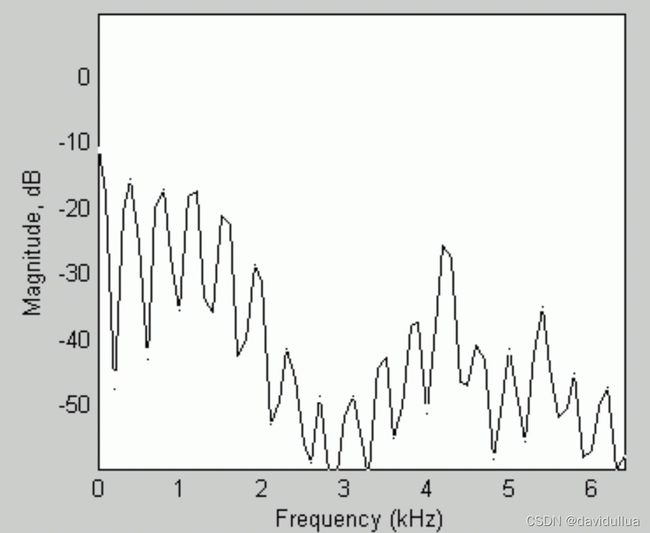
通常我们的作法,是将每一个音框进行频谱分析(Spectral Analysis),算出一个音框讯号如何可以拆解成在不同频率的分量,然后才能进行比对或分析。在频谱分析时,最常用的方法就是「快速傅立叶转换」(Fast Fourier Transform),简称 FFT,这是一个相当实用的方法,可以将在时域(Time Domain)的讯号转换成在频域(Frequency Domain)的讯号,并进而知道每个频率的讯号强度。
比如如下的频谱图 ,横轴是频率,纵轴是计算出来的数值。
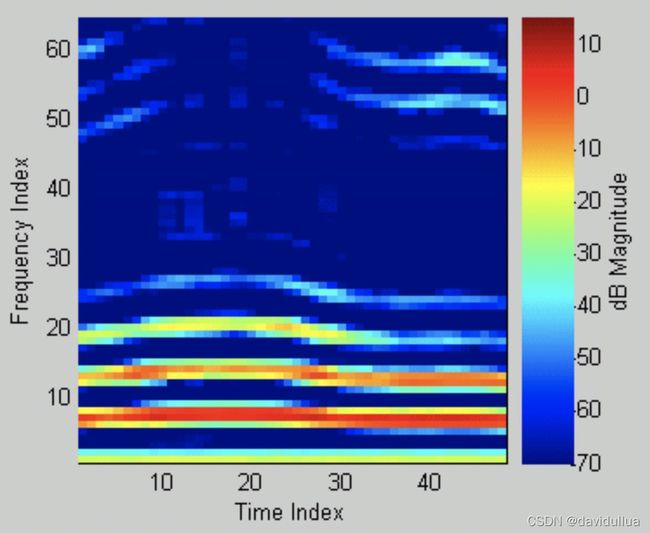
若将频谱图「立」起来,并用不同的颜色代表频谱图的高低,就可以得到频谱对时间所产生的影像,称为 Spectrogram (语谱图),如下
Spectrogram 代表了音色随时间变化的资料,因此有些厉害的人,可以由 Specgrogram 直接看出语音的内容,这种技术称为 Specgrogram Reading