Pesuo-Lidar ++: Accurate Depth for 3D Object Detection in Autonomous Driving 论文笔记

Pseudo-LiDAR++: Accurate Depth for 3D Object Detection in Autonomous Driving

论文链接： https://arxiv.org/abs/1906.06310

一、 Problem Statement

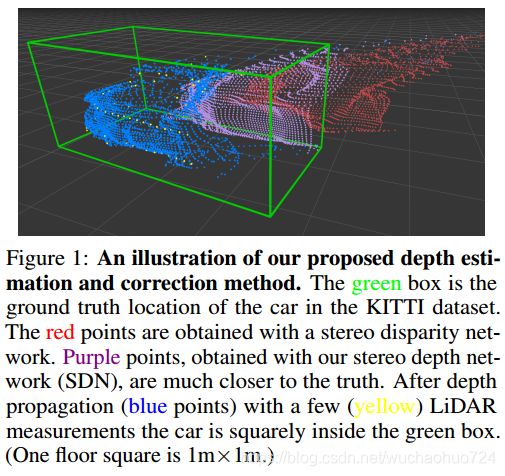
提升pseudo-lidar 检测far-away目标的性能。作者观察到一个问题:双目深度估计的方法是比较可靠的，但是它们估计整个目标的深度不是太近就是太远。

上图红色的点偏离绿色的bounding box 2米，所以深度估计有偏差。而这个偏差主要是因为深度估计不是直接计算的。通常是先计算左右两张图的差异性，然后将其转换为pixel-wise depth map。目前大多数的深度估计方法都专注于修正近处的目标，而远处的目标性能较差。

二、 Direction

1. 通过修改双目深度估计网络的loss function。
2. 利用Lidar sensors 去de-bias 深度估计。
3. 提出depth propagation 算法， 把上面的雷达数据加入到depth map中。

三、 Method

1. Background

简要说明一下什么是pseudo-lidar。当我们有一张估计出来的 深度图$Z(u,v)$ 对应于像素$(u,v)$的时候， 可以通过下面式子转换为3D坐标:
$$z=Z(u,v),x=\frac{(u-C_u)\times z}{f_u},y=\frac{(y-C_v)\times z}{f_v}$$

其中$C_u,C_v$是相机中心，$f_u,f_v$分别是水平和垂直的focal length。而深度图的估计精度对pseudo-lidar检测性能有极大的影响。一般来说，双目的深度估计会比单目深度估计精度高，因此作者主要关注的是双目的深度估计，也就是估计两个图之间的差异性。

首先我们有两张图,$I_l,I_r$，然后有双目摄像头的基线$b$。我们把左图$I_l$作为参考，输出一个差异图(disparity map)$D$,记录相对于右图$I_r$中每一个像素的水平差异。理想状态下，$I_l(u,v)$和$I_r(u+D(u,v),v)$对应于同一个3D位置。 论文写的是$I_r(u,v+D(u,v))$, 个人觉得是typo。

因此我们可以推出 depth map $Z$:
$$Z(u,v)=\frac{f_u\times b}{D(u,v)}$$

估计深度图这个任务就变成了如何估计视差图$D(u,v)$的问题了。 而估计视差图的流程大致是下面两步:

1. 构建一个4D disparity cost volume $C_{disp}$, 维度为:$C_{disp}(u,v,d,:)$。这个$C_{disp}$代表着$I_l(u,v)$和$I_r(u+d,v)$的像素差。
2. 然后根据$C_{disp}$估计每个像素(u,v)的差异$D(u,v)$。

上面的两步通常的做法就是构建一个3D cost volume $C_{disp}(u,v,d)=||I_l(u,v)-I_r(u+d,v)||$，然后最小化$C_{disp}$得到$D(u,v)$，即: $\underset{d}{\mathrm{argmin}}{C}_{disp}(u,v,d)$

在这篇论文中，对于如何获取$D(u,v)$，作者依旧使用PSMNet, 通过下面式子:
$$D(u,v)=\sum _{d}softmax(-S_{disp}(u,v,d))\times d$$
然后进行训练:
$$\sum _{(u,v)\in A}l(D(u,v)-D^{\ast }(u,v))$$

其中$l$是smooth L1 loss。 $D^{\ast }(u,v)$是ground truth map。

2. Stereo Depth Network(SDN)

目前的网络最小化disparity error， 就像上面的式子那样。这样可能会过度强调近处深度小的目标，因此对于远处目标的深度估计表现较差。从上面的式子也可以得出:
$$Z\propto \frac{1}{D}\Rightarrow \delta Z\propto \frac{1}{D^2}\delta D\Rightarrow \delta Z\propto Z^2\delta D$$

也就是说，disparity error $\delta D$ 与 depth error $\delta Z$ 成正比。

作者提出了 两个改变 :

1. 网络直接优化depth loss，而不是disparity loss。
   $$\sum _{(u,v)\in A}l(Z(u,v)-Z^{\ast }(u,v))$$
   这样的话，纠正了过分强调附近物体微小深度误差的现象。

2. 把disparity cost volume 改为 depth cost volume。
   $$Z(u,v)=\sum _{z}softmax(-S_{depth}(u,v,d))\times z$$

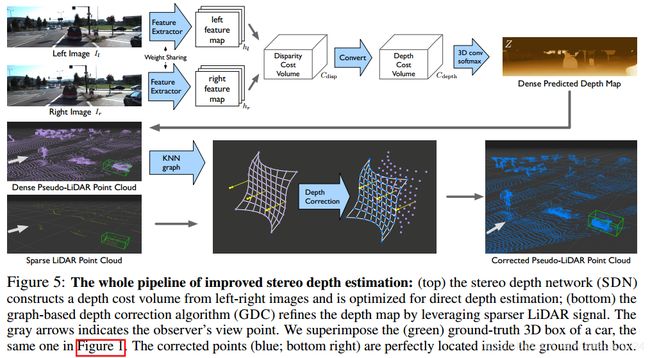
这个$S_{depth}$就通过depth cost colume $C_{depth}(u,v,z,:)$经过3D convolution后获得。而$C_{depth}(u,v,z,:)$是通过$C_{disp}(u,v,\frac{f_u\times b}{z},:)$ bilinear interpolation获得。下图就是具体的流程。

3. Depth Correction

作者提出了graph-based depth correction(GDC)算法把预测出来的pseudo-lidar和实际稀疏的lidar数据进行融合修正。本文不在这个方法上继续探索。

四、 Conclusion

提出了新的loss function来提高深度估计的性能。所提出的利用稀疏雷达数据进行修正提升精度的方法，个人觉得工程上面不太考虑。所以不在本文叙述，而对于网络的提升，值得借鉴。

五、 Reference