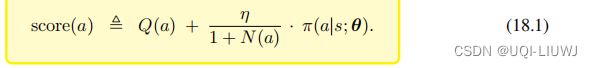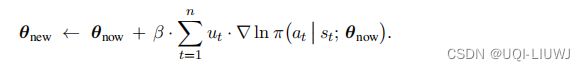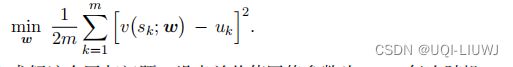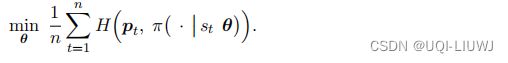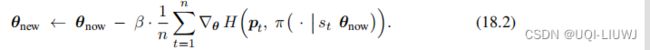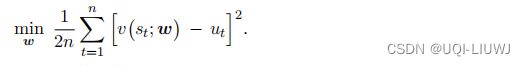强化学习笔记：AlphaGo(AlphaZero) ，蒙特卡洛树搜索（MCTS）

1 AlphaZero的状态

        围棋的棋盘是 19 × 19 的网格，可以在两条线交叉的地方放置棋子，一共有 361 个可以放置棋子的位置，因此动作空间是 A = {1,  · · , 361}。比如动作 a = 123 的意思是在第 123 号位置上放棋子。

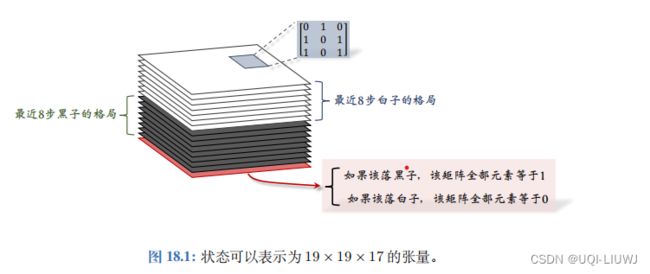
• AlphaGo Zero 使 用 19 ×19 ×17 的张量表示一个状态。
  • 张量每个切片 (Slice) 是 19 ×19 的矩阵，对应 19 ×19 的棋盘。
    • 一个 19 ×19 的矩阵可以表示棋盘上所有黑子的位置。如果一个位置上有黑子，矩阵对应的元素就是1，否则就是 0。
    • 同样的道理，用一个 19 ×19 的矩阵来表示当前棋盘上所有白子的位置。
  • 张量中一共有 17 个这样的矩阵

    • 记录最近 8 步棋盘上黑子的位置，需要 8 个矩阵。
    • 同理，还需要 8 个矩阵记录白子的位置。
    • 还另外需要一个矩阵表示该哪一方下棋；
      • 如果该下黑子，那么该矩阵元素全部等于 1；
      • 如果该下白子， 那么该矩阵的元素全都等于 0。

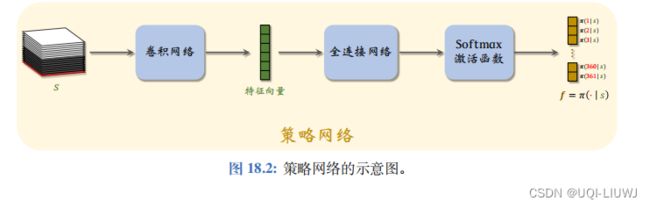
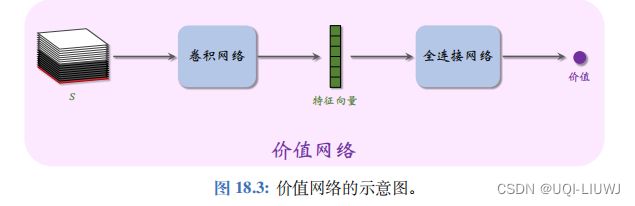
于是我们便有了类似的策略网络和价值网络 

 

 

2 蒙特卡洛树搜索 MCTS

这一小节假设此时已经训练好了策略网络和价值网络 。

AlphaGo 真正跟人下棋的时候，做决策的不是策略网络或者价值网络，而是蒙特卡洛树搜索 (Monte Carlo Tree Search， MCTS) 。

MCTS 不需要训练，可以直接做决策

2.1 基本思想

        和人类下棋类似，AlphaGo在做决策前，需要在“大脑里”做预判，确保几步以后很可能会占优势。如果只根据当前格局做判断，不往前看，是很难获胜的。

• MCTS 的基本思想就是向前看，模拟未来可能发生的情况，从而找出当前最优的动作
  • AlphaGo 每走一步棋，都要用 MCTS 做成千上万次模拟，从而判断出哪个动作的胜算最大。

• 做模拟的基本思想如下。
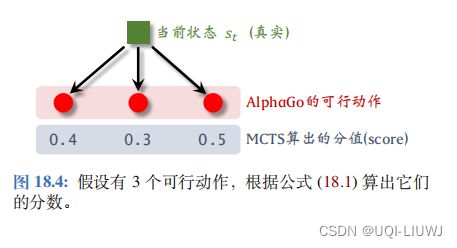
  • 假设当前有三种看起来很好的动作。每次模拟的时候 从三种动作中选出一种，然后将一局游戏进行到底，从而知晓胜负。（只是计算机做模拟 】而已，不是真的跟对手下完一局。）
  • 重复成千上万次模拟，统计一下每种动作的胜负频率， 发现三种动作胜率分别是 48%、56%、52%。
  • 那么 AlphaGo 应当执行第二种动作，因为它的胜算最大。

以上只是 MCTS 的基本想法，实际做起来有很多难点需要解决。

2.2 四个步骤

        MCTS 的每一次模拟选出一个动作 a ，执行这个动作，然后把一局游戏进行到底，用胜负来评价这个动作的好坏。

        MCTS 的每一次模拟分为四个步骤：选择 (Selection) 、扩展 (Expansion)、求值 (Evaluation) 、回溯 (Backup) 。

2.2.1 选择

        观测棋盘上当前的格局，找出所有空位，然后判断其中哪些位置符合围棋规则；每个符合规则的位置对应一个可行的动作。

        每一步至少有几十、甚至上百个可行的动作；假如挨个搜索和评估所有可行动作，计算量会大到无法承受。

        虽然有几十、上百个可行动作，好在只有少数几个动作有较高的胜算。第一步—— 选择——的目的就是找出胜算较高的动作，只搜索这些好的动作，忽略掉其他的动作。

那么，如何判断动作 a 的好坏呢？ 

有两个指标：第一，动作 a 的胜率；第二，策略网络给 动作 a 的“评分”（选择这个动作的概率）。用下面这个分值评价 a 的好坏：

•   η 是个需要调的超参数

• N ( a ) 是动作 a 已经被访问过的次数。

  • 初始的时候，对于所有的 a，令 N(a) ← 0。
  • 动作 a 每被选中一次，我们就把 N(a) 加一：N(a) ← N(a) + 1。  
• Q ( a ) 是之前 N ( a ) 次模拟算出来的动作价值，主要由胜率和价值函数决定。
  • Q ( a ) 的初始值是 0 ；
  • 动作 a 每被选中一次，就会更新一次 Q ( a ) ；如何更新会在第四步说明。

可以这样理解公式 ( 18.1 ) ：

• 如果动作 a 还没被选中过，那么 Q(a) 和 N(a) 都等于零，因此可得
  • 也就是说完全由策略网络评价动作 a 的好坏。
• 如果动作 a 已经被选中过很多次，那么 N ( a ) 就很大，导致策略网络在 score( a ) 中的权重降低。当 N ( a ) 很大的时候，有。
  • 此时主要基于 Q ( a ) 判断 a 的好坏，而策略网络已经无关紧要。
• 系数的另一个作用是鼓励探索，也就是让被选中次数少的动作有更多的机会被选中。假如两个动作有相近的 Q 分数和 π 分数，那么被选中次数少的动作的score 会更高。

MCTS 根据公式 ( 18.1 ) 算出所有动作的分数 score( a ) 。 MCTS 选择分数最高的动作。

图 18.4 的例子中有 3 个可行动作，分数分别为 0 . 4 、 0 . 3 、 0 . 5 。

第三个动作分数最高，会被选中。——>这一轮模拟会执行这个动作（只是模拟而已，不是 AlphaGo 真的走一步棋）。

 

 2.2.2 扩展

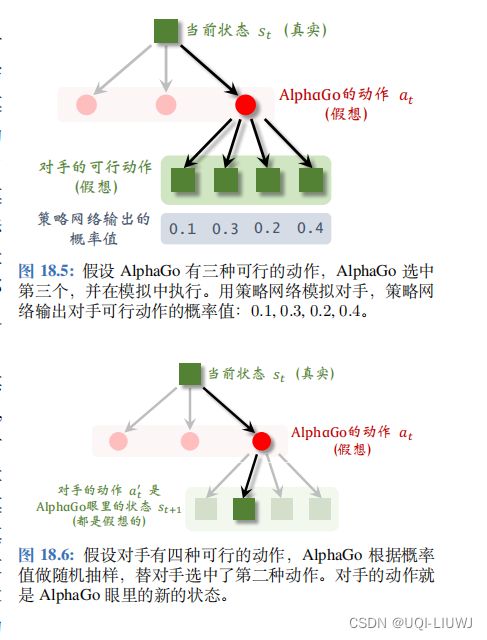
把第一步选中的动作记作 a t ，它只是个假想的动作， 只在“模拟器”中执行，而不是 AlphaGo 真正执行的动作。

AlphaGo 需要考虑这样一个问题：假如它执行动作 a t ，那么对手会执行什么动作呢？

AlphaGo 可以“推己及人”：如果 AlphaGo 认为几个动作很好，对手也会这么认为。

所以 AlphaGo 用策略网络模拟对手， 根据策略网络随机抽样一个动作：

 此处的状态 s′ 是站在对手的角度观测到的棋盘上的格局，动作 a′t 是（假想）对手选择的动作。

图 18.5 的例子中对手有四种可行动作， AlphaGo 用策略网络算出每个动作的概率值，然后根据概率值随机抽样一个对手的动作，记作 a ′ t 。假设根据概率值 0 . 1 , 0 . 3 , 0 . 2 , 0. 4 做随机抽样，选中第二种动作

从 AlphaGo 的角度来看，对手的动作就是 AlphaGo 新的状态。

 

AlphaGo 需要在模拟中跟对 手将一局游戏进行下去，所以需要一个模拟器（即环境）。

在模拟器中，AlphaGo 每执行一个动作，模拟器就会返回一个新的状态。

想要搭建一个好的模 拟器，关键在于使用正确的状态 转移函数 ；如果状态转移函数与事实偏离太远，那么用模拟器做 MCTS 是毫无意义的。

AlphaGo 模拟器利用了 围棋游戏的对称性：AlphaGo 的策略， 在对手看来是状态转移函数；对

手的策略，在 AlphaGo 看来是状态转移函数。

最理想的情况下，模拟器的状态转移函数是对手的真实策略；

然而 AlphaGo 并不知道对手的真实策略。

AlphaGo 退而求其次，用 AlphaGo 自己训练出的策略网络 π 代替对手的策略，作为模拟器的状态转移函数。

 

2.2.3 求值

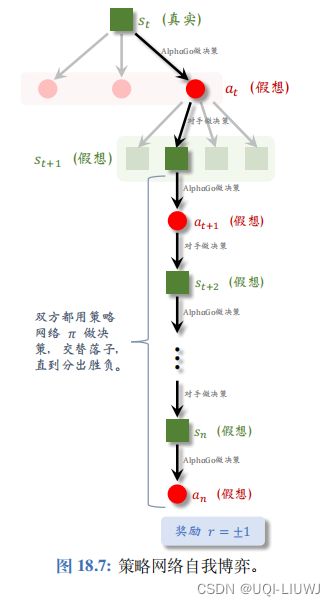
从状态开始，双方都用策略网络 π 做决策，在 模拟器中交替落子，直到分出胜负。

当这局游戏结束时，可以观测到奖励 r 。如果 AlphaGo 胜利，则 r = +1 ，否则 r = 1 。

 

回顾一下，棋盘上真实的状态是，AlphaGo 在模拟器中执行动作 ，然后模拟器中的对手执行动作，带来新的状态。状态 越好，则这局游戏胜算越大。

• 如果 AlphaGo 赢得这局模拟 (r = +1)，则说明可能很好；如果输了 (r = 1)， 则说明可能不好。因此，奖励 r 可 以反映出 的好坏。
• 还可以用价值网络 v 评价状态的好坏。价值 v(; w) 越大，则说明状态越好。

奖励 r 是模拟获得的胜负，是对很可靠的评价，但是随机性太大。

价值网络的评估 v (; w )没有 r 可靠，但是价值网络更稳定、 随机性小。

——>AlphaGo 的解决方案是把奖励 r 与 价值网络的输出 v(; w)取平均，作为对状态的评价

 

 2.2.4 回溯

第三 步——求值——算出了第 t + 1 步某一个状态的价值，记作 V () ；

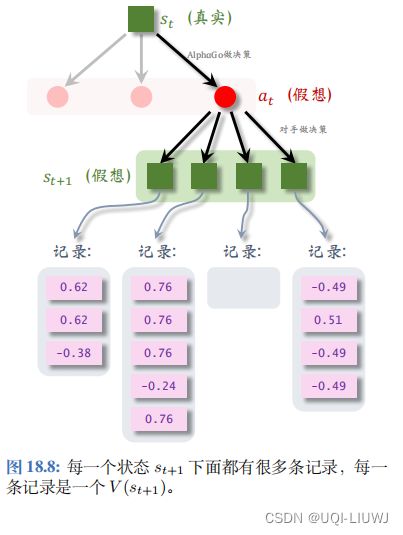
每一次 模拟都会得出这样一个价值，并且记录下来。

模拟会重复很多次，于是第 t + 1 步每一种状态下面可以有多条记 录；如图 18.8 所示。

 

第 t 步的动作 at 下面有多个可能的状态（子节点），每个状态下面有若干条记录。把 a t 下面所有的记录取平均，记作价值 Q( a t)，它可以反映出动作 a t 的好坏。

在图 18.8 中， a t 下面一共有 12 条记录， Q( a t) 是 12 条记录的均值。

给定棋盘上的真实状态 s t ，有多个动作 a 可供选择。对于所有的 a ，价值 Q ( a ) 的初始值是零。

动作 a 每被选中一次（成为 a t ），它下面就会多一条记录，我们就对 Q ( a ) 做一次更新。

2.3 MCTS决策

 

上一小节讲解了单次模拟的四个步骤，注意，这只是单次模拟而已。 MCTS 想要真正做出一个决策（即往真正的棋盘上落一个棋子），需要做成千上万次模拟。在做了无数次模拟之后，MCTS 做出真正的决策：

此时 AlphaGo 才会真正往棋盘上放一个棋子。

为什么要依据 N ( a ) 来做决策呢？

在每一次模拟中，MCTS 找出所有可行的动作{a}， 计算它们的分数 score( a ) ，然后选择其中分数最高的动作，然后在模拟器里执行。

如果某 个动作 a 在模拟中胜率很大，那么它的价值 Q ( a ) 就会很大，它的分数 score( a ) 会很高，

于是它被选中的几率就大。

也就是说如果某个动作 a 很好，它被选中的次数 N ( a ) 就会 大。

 当观测到棋盘上当前状态 st，MCTS 做成千上万次模拟，记录每个动作 a 被选中的次数 N(a)，最终做出决策 at = argmaxa N(a)。

到了下一时刻，状态变成了。MCTS 把所有动作 a 的 Q(a)、N(a) 全都初始化为零，然后从头开始做模拟，而不能利用上一次的结果。

【个人推测，是很难有和St中模拟的一模一样state的了，因为哪怕你当前棋谱是一样的，过去几个片段的棋谱也不可能一样】

 

AlphaGo 下棋非常“暴力”：每走一步棋之前，它先在“脑海里”模拟几千、几万局， 它可以预知它每一种动作带来的后果，对手最有可能做出的反应都在 AlphaGo 的算计之内。

 3 训练策略和价值网络

3.1 AlphaGo 2016 版本的训练

• AlphaGo 2016 版的训练分为三步：
  • 第一，随机初始化策略网络 π(a|s; θ) 之后，用行为克隆 (Behavior Cloning) 从人类棋谱中学习策略网络；
  • 第二，让两个策略网络自我博弈， 用 REINFORCE 算法改进策略网络；
  • 第三，基于已经训练好的策略网络，训练价值网络 v(s; w)。

！！AlphaGo 没有使用MCTS！！

3.1.1 行为克隆

        一开始的时候，策略网络的参数都是随机初始化的。假如此时直接让两个策略网络自我博弈，它们会做出纯随机的动作。它们得随机摸索很多很多次，才能做出合理的动作。假如一上来就用 REINFORCE 学习策略网络，最初随机摸索的过 程要花很久。

        AlphaGo 用行为克隆训练策略网络 π(a|s; θ)模仿学习笔记：行为克隆_UQI-LIUWJ的博客-CSDN博客_行为克隆

··        设361维的向量

         是策略网络的输出

        设是对动作 的 One-Hot 编码。

        函数是交叉熵，衡量和fk的差别。

        行为克隆可以描述为

       这可以想象成分类问题，用梯度下降实现 

 

行为克隆得到的策略网络模仿 高手的动作，可以做出比较合理的决策。它在实战中可以打败业余玩家，但是打不过职业玩家。（因为没有exploration）

为了克服行为克隆的缺点，还需要继续用强化学习训练策略网络。在行为克隆之后再做强化学习改进策略网络，可以击败只用行为克隆的策略网络，胜算是 80% 。

3.1.2 用 REINFORCE 训练策略网络

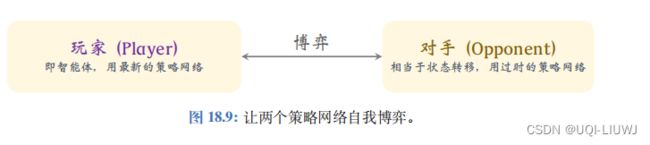
• AlphaGo 让策略网络 做自我博弈，用胜负作为奖励，更新策略网络。
  • 博弈的双方是两个策略网络，一个叫做 “玩家”，用最新的参数，记作 θnow；
  • 另一个叫做“对手”，它的参数是从过时的参数中随机选出来的，记作 θold。
  • “对手”的作用相当于模拟器（环境）的状态转移函数，只是陪玩。
  • 训练的过程中，只更新“玩家”的参数，不更新“对手”的参数。

 

        让“玩家”和“对手”博弈，将一局游戏进行到底，假设走了 n 步。游戏没结束的时候，奖励全都是零：

         游戏结束的时候，如果“玩家”赢了，奖励是 = +1 ，于是所有的回报都是 +1：

        

         游戏结束的时候， 如果“玩家”输了，奖励是 = = 1，于是所有的回报都是 - 1：

        

 

回顾一下REINFORCE的参数更新公式 

3.1.3 训练价值网络

 价值网络 v(s; w) 是对状态价值函数的近似，用于评估状态 s 的好坏。

在完成第二步——训练策略网络 π——之后，用 π 辅助训练 v。

虽然 此处有一个策略网络 π 和一个价值网络 v，但这不属于 Actor-Critic 方法：此处先训练 π，再训练 v，用 π 辅助训练 v；而 Actor-Critic 则是同时训练 π 和 v，用 v 辅助训练 π。

        让训练好的策略网络做自我博弈，记录状态—回报二元组，存到一个数组里。

        自我博弈需要重复非常多次，把最终得到的数据集记作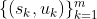

        根据定义， 是对回报的期望

        

        而  价值网络 v(s; w) 是对状态价值函数的近似，所以我们希望用v(s;w)来拟合uk 

于是我们定义回归问题

这也可以用梯度下降实现 

 3.2 AlphaGo Zero 版本的训练

AlphaGo Zero 与 2016 版本的最大区别在于训练策略网络 π ( a | s ; θ ) 方式。

训练 π 的时候，不再从人类棋谱学习，也不用 REINFORCE 方法，而是向 MCTS 学习。

其实可以把 AlphaGo Zero 训练 π 的方法看做是模仿学习，被模仿对象是 MCTS 。

3.2.1 自我博弈

用 MCTS 控制两个玩家对弈。每走一步棋， MCTS 需要做成千上万次模拟，并记录下每个动作被选中的次数 N ( a )

 

设当前是 t 时刻，真实棋盘上当前状态是 s t

现在执行 MCTS ，完成很多次模拟，得到 361 个整数（每种动作被选中的次数）：

 

对这些 N 做归一化，得到的 361 个数，它们相加等于 1 ；把这 361 个数记作 361 维的向量：

设这局游戏走了 n 步之后游戏分出胜负；奖励要么等于 +1 ，要么等于 1 ，取决于游 戏的胜负

在游戏结束的时候，得到回报。记录下这些数据：

 

用这些数据更新策略网络 π 和价值网络 v ；对 π 和 v 的更新同时进行。

3.2.2 更新策略网络

 把 MCTS 的决策作为目标，让 π 去模仿。这是行为克隆，被模仿的对象是MCTS。

我们希望 π 做出的决策

尽量接近pt，也就是希望交叉熵尽量小

定义优化问题：

用梯度下降更新参数：

 

3.2.3 更新策略网络

训练价值网络的方法与 AlphaGo 2016 版本基本一样，都是让 v ( s t ; w ) 拟合回报 u t 。

 

 3.2.4 整体训练流程

 

随机初始化策略网络参数 θ 和价值网络参数 w 。然后让 MCTS 自我博 弈，玩很多局游戏；每完成一局游戏，更新一次 θ 和 w。训练的具体流程就是重复下面 三个步骤直到收敛：