基本遗传算法(GA)详解
遗传算法由John H.Holland教授提出,为一种全局优化算法。它模拟自然进化与遗传理论,通过将优化问题进行转移,从而成功避免了一般优化算法中需要过多考虑的动力学信息问题,在原理上突破了常规的优化算法框架,算法结构较简单、处理信息能力较强,具有很好的鲁棒性。遗传算法最大的特点就是将优化问题中的参数转换成了编码的个体,从而不需要管理优化问题中的参数问题,只需要处理进行了编码的个体,而这些个体在遗传算法优化过程中所描述的就是生物界中“物竞天择,适者生存”的生存抉择概念。正是由于遗传算法具有上述等特点,现在被广泛用于各大领域,比如在一些优化问题复杂多样以及非线性等问题上,是21世纪以来智能算法中的比较突出的技术之一。
Holland教授提出的遗传算法将优化问题转换为遗传问题,通过选择个体编码方式,定义相应的适应度函数,设定收敛条件,经过遗传操作,完成遗传过程。
目前所有改进的遗传算法参考的最原始最基本的是遗传算法框架,因而被称为基本遗传算法。
一、基本概念
1.基因(Gene):是生物界中表现生物体性状特征的一种遗传因子。在遗传算法中,基因的表示方法常常采用二进制(1 0)、整数或者某种字符来进行表达。
2.染色体(Chromosome):是生物界中的生物体表现遗传类特征的一种物质,也就是说它是基因存储的一种载体。
3.个体(Individual):个体所表现出来的是生物体带有特征的实体。在遗传算法进行遗传优化的过程中所优化的基本对象就是个体。
4.种群(Population):个体的集合称为种群。
5.群体规模(Population Size):群体规模表示的是整个种群中所有的个体数量总和。
6.适应度(Fitness):是个体优良的参考值。
7.编码(Coding):DNA中的遗传信息是按某种方式陈列在一个长链上。在遗传算法中,这实际上是一个映射过程,即先验参数到遗传参数的映射。
8.选择(Selection):描述的是“物竞天择,适者生存”的概念。在遗传算法中,参考个体适应值进行选择的过程。
9.复制(Reproduction):即DNA复制。在遗传算法中,对个体进行选择时,往往会根据群体规模来进行优良个体的复制。
10.交叉(Crossover):即杂交,是两个同源染色体在配对时,相互交换基因的过程。在遗传算法中,表示的是两个随机选择的个体进行信息互换的过程。
11.变异(Mutation):细胞在进行复制的时候,会出现很小的概率的差错,使得子染色体与母染色体不同,即发生变异。在遗传算法中,随机性的对个体中的信息进行改变的过程。
遗传算法主要有五个要素组成,分别是染色体编码、适应度函数、遗传算子、终止条件和运行参数。
1)染色体编码
是把一个具体函数优化问题转换为能够处理的搜索空间的问题。编码的设计深深影响着后续运算的有效执行,故而是一个关键。在基本遗传算法中将函数优化问题的参数转换成的个体是用符号集{0、1}来进行表示的,且长度不可变,这种方式称为二进制符号串。
2)适应度函数
是用来评价群体中的个体对环境的生存能力,并以此作为后续对个体进行选择的参考依据。由于遗传算法是概率化的操作,故在设计适应度函数的时候,要充分保证适应度必须为正或者为0,也就是说在特殊情况时需要对目标函数进行转换。
3)遗传算子
是精髓所在,描述生物界遗传机制的算子,包括选择、交叉和变异三种算子。
选择算子:是从当前种群中选择优良个体的过程,是一个优胜劣汰的过程,在基本遗传算法中,采用的是轮盘赌选择原理,即按适应值的比例选择个体。
交叉算子:交叉算子是一种改变解空间的操作,使得整个群体发生质的变化,产生多样性的子空间,具有全局搜索能力的表现形式。在基本遗传算法中,采用的是简单的交叉。
变异算子:变异指个体编码串中的某个基因发生突变,比如:0 -> 1。该算子操作会产生新的形状。
4)终止条件
是一种判断遗传算法在优化迭代过程中何时达到收敛的条件。当遗传代数达到预定的最大遗传代数或者发现种群中个体的状态保持在一个稳定的状态时,可以判定迭代终止;反之,则继续搜索。
5)运行参数
主要有群体规模(N)、最大的终止代数(T)、交叉概率(![]() )和变异概率(
)和变异概率(![]() )。这些运行参数,在实际情况下,并没有合理的相关法则去如何选定,都是根据实际应用中多次的实验取得的经验值。
)。这些运行参数,在实际情况下,并没有合理的相关法则去如何选定,都是根据实际应用中多次的实验取得的经验值。
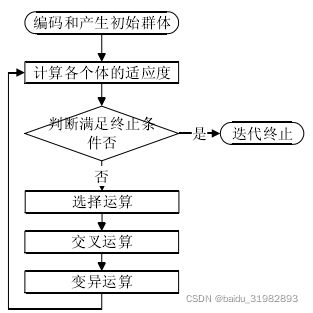
二、基本遗传算法的流程
基本遗传算法的框架是最简单的,也是所有后续改进的基础,下图为流程图:
1) 编码和产生初始群体
根据优化函数的实际问题,选择好相应的编码方法,根据种群规模的需要,随机产生确定长度的n个染色体,作为初始种群。
![]()
2)计算适应度值
假设适应度函数为![]() ,则对所有的个体计算其相对应的值为:
,则对所有的个体计算其相对应的值为:
![]()
3)终止判断
根据设定的终止条件判断是否达到收敛状态以选择下一步操作。
4)选择运算
选择适应度值大的个体进行交叉运算,则每个个体的选择概率为![]() :
:
以选择概率![]() 作为新的概率分布,从当前种群中选择个体重组新的个体种群
作为新的概率分布,从当前种群中选择个体重组新的个体种群![]() :
:
![]()
5)交叉运算
随机从种群中选择两个不同的个体,以概率![]() 进行交换基因,得到新的两个个体,进行
进行交换基因,得到新的两个个体,进行![]() 次1,得到一个新的种群
次1,得到一个新的种群![]() 。
。
6)变异运算
从种群中随机选择个体,以变异概率![]() 进行染色体变异,得到新的种群
进行染色体变异,得到新的种群![]() ,这个群体作为完成一次遗传操作的子种群,即
,这个群体作为完成一次遗传操作的子种群,即![]() ,此时传到第 2)步。
,此时传到第 2)步。
三、相关问题
基本遗传算法自问世以来,由于其具有隐含并行性和全局搜索性两个主要的特点,使其很快的便应用到各个领域中,但是就在其应用广泛的同时,基本遗传算法所暴露出来的缺点也备受关注,主要有以下几点:
1.基本遗传算法采用的编码方式为二进制编码,对于一些特殊函数,很可能得不到很好的表达,达不到该有的精度。
2.基本遗传算法采用的是轮盘赌的基于适应值比例的选择策略。当在遗传进化的初期,适应度值分布杂乱,适应度值过大的个体被选中进入交叉、变异概率高,而适应度值偏小的个体不易被选中,这样的群体多样性必然下降迅速,导致算法嵌入局部最优,当进入后期时,适应度值分布均匀,从而搜索能力减弱,收敛速度将陷入停滞。
3.基本遗传算法采用单点交叉和基于位变异的遗传算子,使得不能充分发挥全局搜索的优点,容易导致“早熟”现象。
4.基本遗传算法中的运行参数交叉与变异概率保持在一个设定值不变,导致适应值大的个体染色体容易被破坏,小的则容易被保存下来,对整体遗传运算不利。
基于python实现遗传算法,可以参见本人之前的博客。