pytorch基础(十一)- 生成对抗网络
目录
- 生成对抗网络原理
- 纳什均衡
- JS散度的缺陷
- EM距离
- GAN实战
- WGAN实战
生成对抗网络原理
我们无法知道数据的真实分布是什么,如何用数学公式表达;
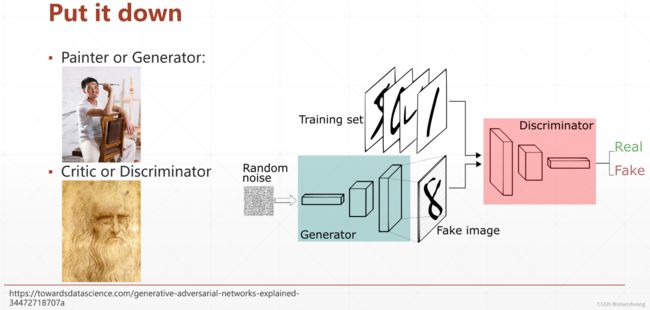
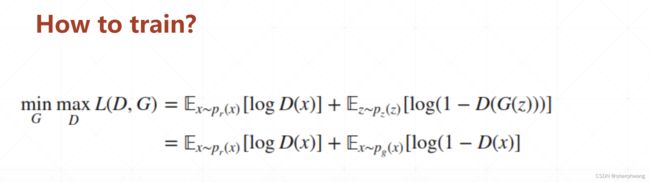
实际训练时Discriminator和Generator的损失如下:

纳什均衡
GAN当固定Generator时,最优的D为:

当固定Discriminator时,整个网络的损失为:
此时L(G,D)等同于真实数据和虚假数据之间的2倍JS散度减去一个常量值2log2,这会导致在固定D训练G时,由于JS散度的缺陷而造成整个网络的梯度趋近于0,从而参数得不到更新。

JS散度的缺陷
2014年发现GAN的训练非常不稳定。原因如下:
使用JS散度衡量输出分布和真实分布的距离,当两个分布完全不重叠的时候,等于任意的x输入,JS散度值等于log2。那么在固定D从而训练G时(此时网络损失和JS散度呈线性关系),由于训练数据和虚假数据的分布不重叠,从导致JS散度值固定为一个常量值,从而网络的损失也固定为一个常量值,从而网络参数梯度为0,参数得不到更新,训练不稳定。
EM距离
解决上述由于训练数据和虚假数据分布不重叠而导致的网络训练不稳定的问题,可以使用Wssserstein距离替代原来JS散度的损失。
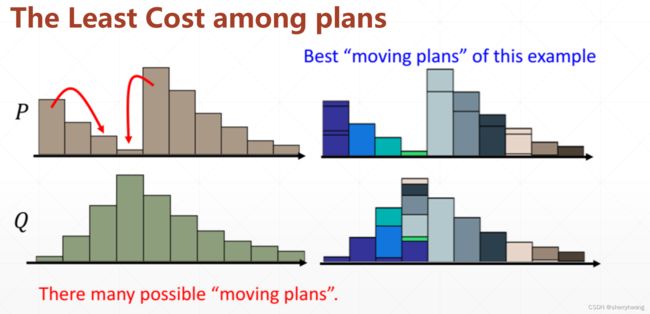
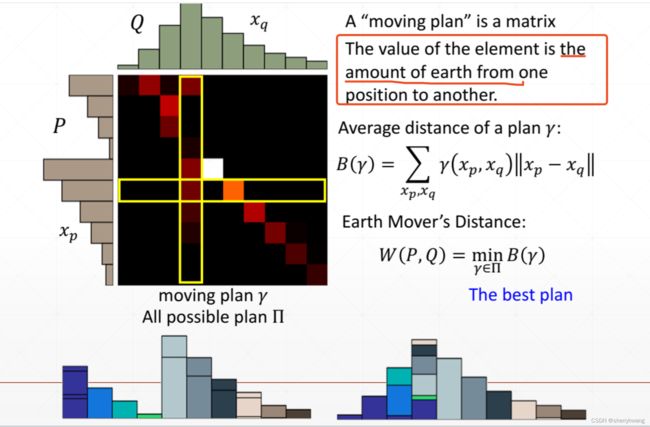

GAN实战
训练数据:8个二维高斯分布的随机生成数据;
GAN:根据随机噪声,模拟生成这8个高斯分布的数据;
比如一个batch包含8个高斯分布的数据,一次训练过程要求根据batch个随机噪声,也生成8个同样高斯分布的数据。
import torch
from torch import nn, optim, autograd
import numpy as np
import visdom
import random
h_dim = 400
batchsz = 512
viz = visdom.Visdom()
class Generator(nn.Module):
def __init__(self, h_dim):
super().__init__()
self.net = nn.Sequential(
nn.Linear(2, h_dim),
nn.ReLU(inplace=True),
nn.Linear(h_dim, h_dim),
nn.ReLU(inplace=True),
nn.Linear(h_dim, h_dim),
nn.ReLU(inplace=True),
nn.Linear(h_dim, 2)
)
def forward(self, x):
return self.net(x)
class Discriminator(nn.Module):
def __init__(self, h_dim):
super().__init__()
self.net = nn.Sequential(
nn.Linear(2, h_dim),
nn.ReLU(inplace=True),
nn.Linear(h_dim, h_dim),
nn.ReLU(inplace=True),
nn.Linear(h_dim, h_dim),
nn.ReLU(inplace=True),
nn.Linear(h_dim, 1), #输出分类概率
nn.Sigmoid()
)
def forward(self, x):
return self.net(x).view(-1)
def data_gernerator():
scale = 2
centers = [(1,0),(-1,0),(0,1),(0,-1),
(1. / np.sqrt(2), 1. / np.sqrt(2)),
(1. / np.sqrt(2), -1. / np.sqrt(2)),
(-1. / np.sqrt(2), 1. / np.sqrt(2)),
(-1. / np.sqrt(2), -1. / np.sqrt(2))]
centers = [(scale * x, scale * y) for x,y in centers]
while True:
dataset = []
for i in range(batchsz):
point = np.random.randn(2) * 0.02 #随机采样两个数据
center = random.choice(centers) #从八个高斯分布中随机选一个
# N(0,1) + center_x1/x2 加上一个均值,方差还是为1
point[0] += center[0]
point[1] += center[1]
dataset.append(point)
dataset = np.array(dataset).astype(np.float32)
dataset /= 1.414
yield dataset #保存状态,返回dataset,下次运行时又继续从while处开始执行
def main():
# 固定随机性
torch.manual_seed(23)
np.random.seed(23)
data_iter = data_gernerator()
x = next(data_iter)
# print(x.shape) [b, 2]
G = Generator(h_dim)
D = Discriminator(h_dim)
optim_G = optim.Adam(G.parameters(), lr = 5e-4, betas=(0.5, 0.9))
optim_D = optim.Adam(D.parameters(), lr = 5e-4, betas=(0.5, 0.9))
for epoch in range(50000):
# Generator 和 Discriminator交替训练
# 一般先训 Discrimator
# 1. train Discriminator firstly, max(D(x)), min(D(G(z)))
for _ in range(5):
# 1.1 train on real data
x = next(data_iter)
x = torch.from_numpy(x)
pred_real = D(x) #真实数据的判决结果
loss_real = -pred_real.mean() # max pred_real
# 1.2 train on fake data
z = torch.randn(batchsz, 2) #随机生成噪声
x_fake = G(z).detach() #根据噪声生成假的数据 tf.stop_gradient()
pred_fake = D(x_fake) #假的数据的判决结果
loss_fake = pred_fake.mean()
# 1.3 aggreate loss
loss_D = loss_real + loss_fake #最大化真实数据的判决概率, 最小化生成数据的判决概率
# 1.4 optimize
optim_D.zero_grad()
loss_D.backward()
optim_D.step()
# 2. train Generator, max D(G(z))
z = torch.randn(batchsz, 2) #随机生成噪声
x_fake = G(z) #不能detach, 因为D在G后面
pred_fake = D(x_fake) # D和G都有梯度反向传播,但只有G更新
loss_G = - pred_fake.mean() # 最大化生成数据的判决概率
# optimize
optim_G.zero_grad()
loss_G.backward() #反向传播计算G和D的梯度
optim_G.step() #只更新G的参数
if epoch % 100 == 0:
print(loss_D.item(), loss_G.item())
#会出现 0.0, -1.0两个值
# 原因是Discriminator训练得很好,可以很好地将真假数据区分开来, 所以loss为0
# 但由于Generator训练过程中, 使用JS散度不能衡量两个没有重叠的分布,使得网络没有梯度信息,
# Generator长期得不到更新,所以loss长期处于-1.0.
if __name__ == '__main__':
main()
输出:
-0.14626020193099976 -0.47136804461479187
0.0 -1.0
0.0 -1.0
0.0 -1.0
0.0 -1.0
0.0 -1.0
0.0 -1.0
0.0 -1.0
...
分析:从D和G在训练过程中产生的损失来看,loss_D稳定为0,说明Discriminator可以将真假数据区分得很好,因为数据比较简单。loss_G稳定为-1.0,原因是因为JS散度在两个数据分布不重叠的情况,它为一个固定值,导致网络梯度得不到更新(训练G时,固定D,此时的G的损失等于2倍Pr和Pg的JS散度减去2log2)。
WGAN实战
在GAN中对Discriminator对输入数据的梯度进行惩罚。
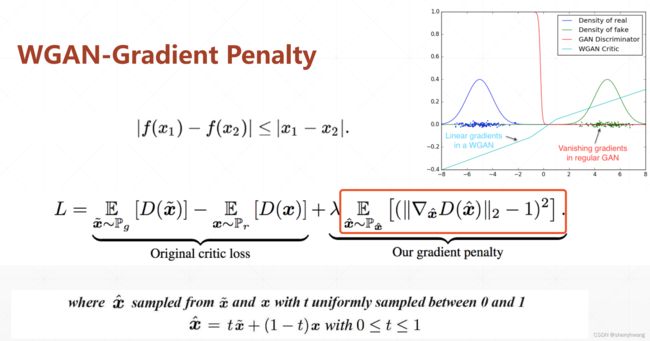
from re import L
import torch
from torch import nn, optim, autograd
import numpy as np
import visdom
import random
h_dim = 400
batchsz = 512
viz = visdom.Visdom()
class Generator(nn.Module):
def __init__(self, h_dim):
super().__init__()
self.net = nn.Sequential(
nn.Linear(2, h_dim),
nn.ReLU(inplace=True),
nn.Linear(h_dim, h_dim),
nn.ReLU(inplace=True),
nn.Linear(h_dim, h_dim),
nn.ReLU(inplace=True),
nn.Linear(h_dim, 2)
)
def forward(self, x):
return self.net(x)
class Discriminator(nn.Module):
def __init__(self, h_dim):
super().__init__()
self.net = nn.Sequential(
nn.Linear(2, h_dim),
nn.ReLU(inplace=True),
nn.Linear(h_dim, h_dim),
nn.ReLU(inplace=True),
nn.Linear(h_dim, h_dim),
nn.ReLU(inplace=True),
nn.Linear(h_dim, 1), #输出分类概率
nn.Sigmoid()
)
def forward(self, x):
return self.net(x).view(-1)
def data_gernerator():
scale = 2
centers = [(1,0),(-1,0),(0,1),(0,-1),
(1. / np.sqrt(2), 1. / np.sqrt(2)),
(1. / np.sqrt(2), -1. / np.sqrt(2)),
(-1. / np.sqrt(2), 1. / np.sqrt(2)),
(-1. / np.sqrt(2), -1. / np.sqrt(2))]
centers = [(scale * x, scale * y) for x,y in centers]
while True:
dataset = []
for i in range(batchsz):
point = np.random.randn(2) * 0.02 #随机采样两个数据
center = random.choice(centers) #从八个高斯分布中随机选一个
# N(0,1) + center_x1/x2 加上一个均值,方差还是为1
point[0] += center[0]
point[1] += center[1]
dataset.append(point)
dataset = np.array(dataset).astype(np.float32)
dataset /= 1.414
yield dataset #保存状态,返回dataset,下次运行时又继续从while处开始执行
def gradient_penalty(D, x_real, x_fake): #dskj1
t = torch.rand(batchsz, 1) #随机sample
# [b,1]=>[b,2]
t = t.expand_as(x_real)
x = t*x_real + (1-t)*x_fake #真实数据和fake数据之间做一个线性插值
x.requires_grad_() #设置x需要导数信息
pred = D(x)
grads = autograd.grad(outputs = pred, inputs=x,
grad_outputs=torch.ones_like(pred),
create_graph=True, #用于二阶求导
retain_graph=True, #如果还需要backward一次,就把这个梯度信息保留下来,否则会报错
only_inputs=True
)[0]
gp = torch.pow((grads.norm(2, dim = 1) -1), 2).mean()
return gp
def main():
# 固定随机性
torch.manual_seed(23)
np.random.seed(23)
data_iter = data_gernerator()
x = next(data_iter)
# print(x.shape) [b, 2]
G = Generator(h_dim)
D = Discriminator(h_dim)
optim_G = optim.Adam(G.parameters(), lr = 5e-4, betas=(0.5, 0.9))
optim_D = optim.Adam(D.parameters(), lr = 5e-4, betas=(0.5, 0.9))
for epoch in range(50000):
# Generator 和 Discriminator交替训练
# 一般先训 Discrimator
# 1. train Discriminator firstly, max(D(x)), min(D(G(z)))
for _ in range(5):
# 1.1 train on real data
x = next(data_iter)
x = torch.from_numpy(x)
pred_real = D(x) #真实数据的判决结果
loss_real = -pred_real.mean() # max pred_real
# 1.2 train on fake data
z = torch.randn(batchsz, 2) #随机生成噪声
x_fake = G(z).detach() #根据噪声生成假的数据 tf.stop_gradient()
pred_fake = D(x_fake) #假的数据的判决结果
loss_fake = pred_fake.mean()
# 1.3 gradient penalty
gp = gradient_penalty(D, x, x_fake.detach()) #这里x_fake要detach一下,因为不需要对它进行求导
# 1.4 aggreate loss
loss_D = loss_real + loss_fake + 0.2 * gp #最大化真实数据的判决概率, 最小化生成数据的判决概率
# 1.4 optimize
optim_D.zero_grad()
loss_D.backward()
optim_D.step()
# 2. train Generator, max D(G(z))
z = torch.randn(batchsz, 2) #随机生成噪声
x_fake = G(z) #不能detach, 因为D在G后面
pred_fake = D(x_fake) # D和G都有梯度反向传播,但只有G更新
loss_G = - pred_fake.mean() # 最大化生成数据的判决概率
# optimize
optim_G.zero_grad()
loss_G.backward() #反向传播计算G和D的梯度
optim_G.step() #只更新G的参数
if epoch % 100 == 0:
print(loss_D.item(), loss_G.item())
#会出现 0.0, -1.0两个值
# 原因是Discriminator训练得很好,可以很好地将真假数据区分开来, 所以loss为0
# 但由于Generator训练过程中, 使用JS散度不能衡量两个没有重叠的分布,使得网络没有梯度信息,
# Generator长期得不到更新,所以loss长期处于-1.0.
if __name__ == '__main__':
main()
输出:
0.010273948311805725 -0.4702531099319458
-0.5763486623764038 -0.1938347965478897
-0.20412319898605347 -0.4627363085746765
-0.21898901462554932 -0.4972558617591858
-0.13111859560012817 -0.504425048828125
-0.1431763768196106 -0.4709075689315796
-0.09945613145828247 -0.5348900556564331
...
WGAN的训练过程比GAN稳定许多。

