pytorch基础（四）- 神经网络与全连接
目录
- Logistic Regression
- 交叉熵
- 多分类问题
- 全连接层
- 激活函数与GPU加速
-
- 不同激活函数
- GPU加速
- 模型测试
- Visdom可视化
-
- 介绍
- 安装
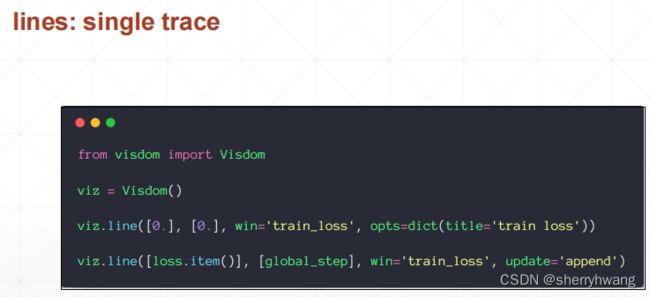
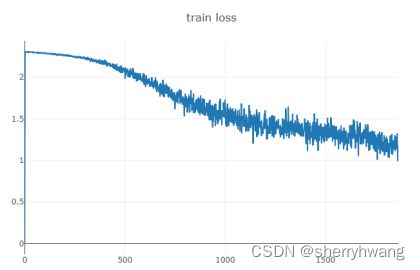
- visdom画一条线
- visdom画多条线
- visdom直接展示tensor类型图像，和label
Logistic Regression
逻辑回归用于分类问题的预测。
为什么分类问题不用以最小化准确率的目标来训练?
可能会出现梯度消失或者梯度爆炸的问题。
为什么要叫逻辑回归，而不是分类？
二分类问题：
多分类问题：
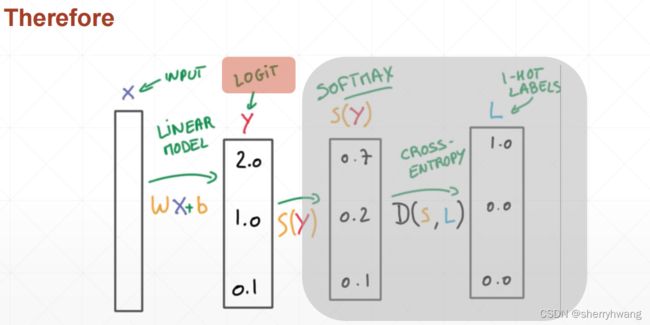
多分类问题搭配softmax
softmax使预测较大的值相对更大
交叉熵
跟softmax匹配的loss交叉熵
熵越高，代表信息越稳定，惊喜度越低。
熵越低，代表不确定性高，惊喜度高。
代码测试
import torch
import torch.nn.functional as F
a = torch.full([4], 1/4)
entropy = (-a * torch.log2(a)).sum()
print(entropy)
a = torch.tensor([0.1, 0.1, 0.1, 0.7])
entropy = (-a * torch.log2(a)).sum()
print(entropy)
a = torch.tensor([0.001, 0.001, 0.001, 0.997])
entropy = (-a * torch.log2(a)).sum()
print(entropy)
输出：
tensor(2.)
tensor(1.3568)
tensor(0.0342)
当p是one-hot编码的时候，交叉熵等于KL散度。
二分类问题的交叉熵形式：
交叉熵相比于MSE的梯度更大，
F.cross_entropy是集softmax，log sum， nll_loss一体的。
代码：
import torch
import torch.nn.functional as F
x = torch.randn((1, 784))
w = torch.randn((10, 784))
b = torch.randn((1, 10))
y = x@w.t() + b
print(y.shape)
loss = F.cross_entropy(y, torch.tensor([4]))
print(loss.item())
pred = F.softmax(y, dim=1)
pred_log = torch.log(pred)
print(pred_log.shape)
loss = F.nll_loss(pred_log, torch.tensor([4]))
print(loss.item())
输出：
torch.Size([1, 10])
73.18791198730469
torch.Size([1, 10])
73.18791198730469
多分类问题
使用MLP对MINIST数据集进行多分类预测。
import torch
import torch.nn as nn
import torch.nn.functional as F
from torchvision import datasets, transforms
w1, b1 = torch.randn(200, 784, requires_grad=True),\
torch.zeros(200, requires_grad=True)
w2, b2 = torch.randn(200, 200, requires_grad=True),\
torch.zeros(200, requires_grad=True)
w3, b3 = torch.randn(10, 200, requires_grad=True),\
torch.zeros(10, requires_grad=True)
torch.nn.init.kaiming_normal_(w1)
torch.nn.init.kaiming_normal_(w2)
torch.nn.init.kaiming_normal_(w3)
def forward(x):
x = x@w1.t() + b1
x = F.relu(x)
x = x@w2.t() + b2
x = F.relu(x)
x = x@w3.t() + b3
x = F.relu(x) #这里不激活也可以
return x
optimizer = torch.optim.SGD([w1,b1,w2,b2,w3,b3], lr = 1e-2)
criteon = nn.CrossEntropyLoss()
epoches = 10
batch_size = 200
minist_train = datasets.MNIST('../data', train=True, download=True, transform=transforms.Compose([
transforms.ToTensor(),
transforms.Normalize((0.1307,), (0.3081,))]
))
minist_val = datasets.MNIST('../data', train=False, download=True, transform=transforms.Compose([
transforms.ToTensor(),
transforms.Normalize((0.1307,), (0.3081,))]
))
train_loader = torch.utils.data.DataLoader(minist_train, batch_size = batch_size, shuffle=True)
val_loader = torch.utils.data.DataLoader(minist_val, batch_size = batch_size, shuffle = False)
for epoch in range(epoches):
for batch_idx, (data, target) in enumerate(train_loader):
data = data.view(-1, 28*28)
logits = forward(data)
loss =criteon(logits, target)
optimizer.zero_grad()
loss.backward()
optimizer.step()
if batch_idx % 100 == 0:
print('Train epoch: {} [{}/{} ({:.0f}%)]\tLoss: {:.6f}'.format(epoch, \
batch_idx*len(data), len(train_loader.dataset), 100. *batch_idx/len(train_loader),
loss.item()))
test_loss = 0
total_correct = 0
for data, target in val_loader:
data = data.view(-1, 28*28)
logits = forward(data) #(N, classes)
loss = criteon(logits, target)
test_loss += loss.item()
pred = logits.data.max(dim=1)[1]
correct = pred.eq(target.data).sum()
total_correct += correct
test_loss /= len(val_loader.dataset)
accuracy = total_correct / len(val_loader.dataset)
print('\nTest set: Average loss: {:.4f}, Accuracy: {}/{} ({:.0f}%)\n'.format(
test_loss, total_correct, len(val_loader.dataset),
100. * accuracy))
输出：
...
Train epoch: 7 [0/60000 (0%)] Loss: 0.188797
Train epoch: 7 [20000/60000 (33%)] Loss: 0.157730
Train epoch: 7 [40000/60000 (67%)] Loss: 0.153730
Test set: Average loss: 0.0008, Accuracy: 9513/10000 (95%)
Train epoch: 8 [0/60000 (0%)] Loss: 0.242635
Train epoch: 8 [20000/60000 (33%)] Loss: 0.092858
Train epoch: 8 [40000/60000 (67%)] Loss: 0.165861
Test set: Average loss: 0.0008, Accuracy: 9540/10000 (95%)
Train epoch: 9 [0/60000 (0%)] Loss: 0.099372
Train epoch: 9 [20000/60000 (33%)] Loss: 0.118166
Train epoch: 9 [40000/60000 (67%)] Loss: 0.155070
Test set: Average loss: 0.0007, Accuracy: 9556/10000 (96%)
全连接层
代码：
class MLP(nn.Module):
def __init__(self):
super(MLP, self).__init__()
self.model = nn.Sequential(
nn.Linear(784,200),
nn.ReLU(inplace=True),
nn.Linear(200,200),
nn.ReLU(inplace=True),
nn.Linear(200,10),
nn.ReLU(inplace=True),
)
def forward(self, x):
return self.model(x)
mlp = MLP()
optimizer = torch.optim.SGD(mlp.parameters(), lr = 1e-2)
激活函数与GPU加速
不同激活函数
sigmoid函数容易出现梯度弥散的情况，输出值过大或者过小会导致梯度区域0，参数更新保持不变。所以网络层中能不使用sigmoid的地方就尽量不要使用sigmoid。
tanh函数也会出现梯度弥散的情况。
Relu函数缓解了sigmoid梯度弥散的情况。当输出值大于0的时候，梯度为1，计算非常简单。ReLU依然存在梯度弥散的情况，当输出值小于0时，梯度为0。
LeakyReLU解决ReLU梯度弥散的问题。
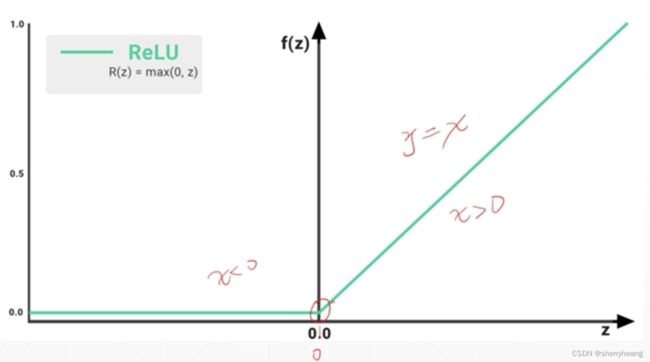
ReLU函数数学上在0处不连续的，SELU为解决这个问题而提出。
softplus也是为了解决ReLU在0值处不连续的情况。
GPU加速
device = torch.device(‘cpu’) / torch.device(‘cuda:0’)
将数据放到指定设备上去，新的数据和原来的数据不共享内存，而是新开辟了内存；
data = data.to(device)
将模型放到指定设备上去，新的模型和原来的模型共享一个内存，是inplace操作；
model = model.to(device)
data = data.cpu() 将数据放在cpu上
model = model.cpu() 将模型放在cpu上
data = data.gpu() 将数据放在gpu上
model = modek.gpu() 将模型放在gpu上
模型测试
argmax(logits, dim=1)返回多分类问题预测的标签
torch.eq(pred_label, label) 得到预测的标签是否正确
import torch
import torch.nn.functional as F
logits = torch.rand((4,10))
print(logits.argmax(dim = 1))
print(logits.max(dim = 1))
pred = F.softmax(logits, dim = 1)
print(pred.shape)
pred_label = pred.argmax(dim = 1)
label = torch.tensor([9,0,3,4])
correct = torch.eq(pred_label, label)
print('correct:',correct)
accuracy = correct.sum().float().item() / 4
print('accuracy:', accuracy)
输出：
tensor([8, 8, 6, 4])
torch.return_types.max(
values=tensor([0.9408, 0.7805, 0.9484, 0.8609]),
indices=tensor([8, 8, 6, 4]))
torch.Size([4, 10])
correct: tensor([False, False, False, True])
accuracy: 0.25
Visdom可视化
介绍
TensorBoard是TensorFlow提供的可视化工具。
在pytorch中也有类似的可视化工具TensorBoardX。
visdom是pytorch提供的可视化工具。
安装
visdom安装:
pip install visdom
启动visdom监听进程：
python -m visdom.server
测试代码：
from matplotlib.pyplot import title
from visdom import Visdom
viz = Visdom()
viz.line([0.],[0.], win='train_loss', opts=dict(title='train loss'))
访问http://localhost:8097/
visdom画一条线
visdom画多条线
visdom直接展示tensor类型图像，和label
