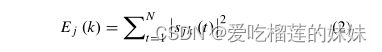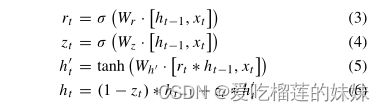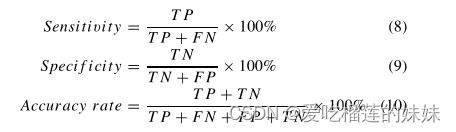024 基于双向门控递归单元网络的癫痫发作检测2022

Epileptic Seizure Detection Based on Bidirectional Gated Recurrent Unit Network

abstract

长期脑电(EEG)的目测是神经科医生的一项繁琐工作。为了方便癫痫的诊断和治疗，提出了一种基于双向门控递归单元(bi-GRU)神经网络的癫痫自动检测方法。首先，将小波变换应用于脑电信号的滤波预处理。然后计算信号在几个特定频段的相对能量，并将其输入到BiGRU网络。然后，对bi-GRU网络的输出进行滑动平均滤波、阈值比较和癫痫合并处理，得到被测脑电信号是否属于癫痫的判别结果。在CHB-MIT头皮EEG数据库上进行评估，该癫痫检测方法的平均灵敏度为93.89%，平均特异度为98.49%。在867.14 h的测试数据上，128次癫痫发作中有124次被正确检测，平均误检率为0.31次/h。结果表明，BiGRU网络在癫痫发作检测中具有一定的优势，该检测方法在脑电长期监测中具有广阔的应用前景。

Introduction

本文提出了一种基于时频分量相对能量和双向门控回归单元(bi-GRU)神经网络的癫痫检测方法。作为递归神经网络的一种，GRU网络能够有效地捕捉长序列中的长期依赖关系，在结构和计算代价上具有优势与长短期记忆(LSTM)网络[28]-[34]等其他RNN网络相比，癫痫发作是一个动态的演化过程，未来的EEG信息可能有助于当前EEG的模式识别，本文设计了一种BiGRU网络结构的癫痫发作检测方法。

BiGRU网络通过在反向传播GRU块中加入隐含层，对脑电信号进行正反向分析，提高了检测性能。在公共和临床脑电数据库上的实验结果表明，基于BiGRU的癫痫发作检测方法具有结构简单、计算代价低、挖掘长期脑电信号依赖信息的能力强等优点。

本文的其余部分组织如下。第二节介绍了这项工作中使用的脑电数据库。第三节重点介绍了本文提出的癫痫发作检测方法和采用的性能评价方法。第四节展示了评估结果，第五节讨论了拟议的癫痫检测方法。最后，第六节给出了本文的结论。

II. DATABASE

这项工作中使用的脑电数据部分来自CHB-MIT头皮脑电数据库，该数据库由波士顿儿童医院收集[35]，[36]。在脑电数据采集过程中，采用国际通用的10-20脑电电极位置测量系统，采样率为256赫兹，分辨率为16位。在CHB-MIT数据库中收集了23例癫痫患者的脑电记录，并将其归类为24例，其中病例chb21和chb01来自同一受试者，相隔1.5年。除了属于病例chb04、chb06、chb07、chb09、chb10和chb23的一些文件是两个或四个小时长之外，对于每个病例，大约有9到42个连续的EEG文件可用，并且大多数文件包含一个小时的EEG记录。该数据库中的脑电文件共包括198次癫痫发作，并对每次发作的开始和结束进行了注释。本工作中使用的CHB-MIT脑电数据的详细信息如表I所示。

对于每个案例，我们构建了非重叠的训练和测试数据集，分别用于建立和评估癫痫发作检测系统。除了选择1~5次癫痫发作的脑电作为训练数据外，非癫痫发作的脑电也包括在训练数据集中。训练数据集中的非癫痫脑电信号的数量等于或等于癫痫脑电信号的2-4倍。总共约198.14分钟的脑电记录被用作24例的训练数据。此外，以其余脑电记录作为测试数据，总持续时间为867.14 h，包括128次发作。

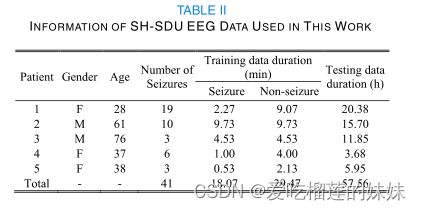
另一部分脑电数据来自山东大学第二医院的5例癫痫患者，分别来自山东大学济南第二医院、中国。在总共58.40h的头皮脑电记录中，包含了41次癫痫发作，并已被临床专家标记。对于每个患者，按照与CHB-MIT数据库相同的方法构建训练集和测试集。训练数据的总时长为47.54分钟，测试数据的时长为57.56小时。在训练集和测试集中得发作次数分别是12和29次。表二给出了SH-SDU数据集的详细信息。

III. METHOD

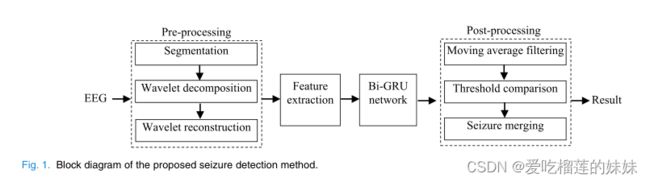
本文提出的癫痫发作检测方法的框图如图1所示，包括脑电信号的预处理、特征提取、基于双GRU神经网络的分类模型和后处理。下面对检测方法的各个部分进行详细说明。

A. Pre-Processing

在预处理阶段，首先利用4s的滑动时间窗对连续的脑电信号进行无重叠分割，然后对分割后的脑电信号进行小波变换。作为一种时频分析方法，离散小波变换将脑电信号分解为细节系数和近似系数，以表征信号在不同时频区域的分量[37]。本文采用Daubechies-4小波作为小波函数，对脑电信号进行5个尺度的分解。对于采样率为256 Hz的脑电信号，5个尺度上的细节系数分别代表了64~128 Hz、32~64 Hz、16~32 Hz、8~16 Hz和4~8 Hz频段的信号分量。显然，小波尺度3、4和5的频带与癫痫活动的频带基本一致，主要在3-30赫兹[5]范围内。在这三个尺度上选取细节系数进行单尺度信号重构和特征提取，重构后的信号与原始脑电信号长度相等。

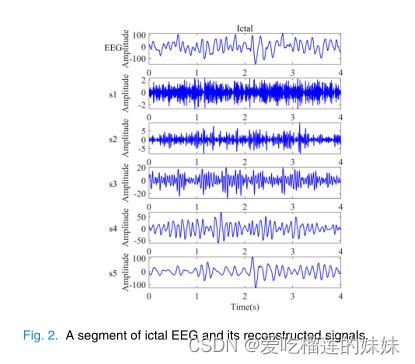
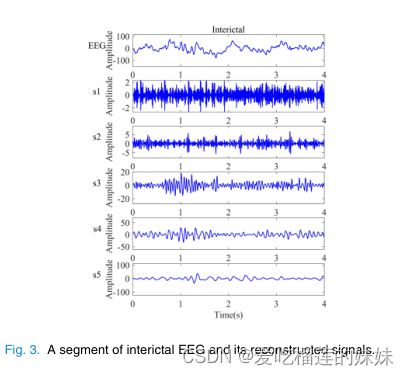
图2和图3说明了EEG的两个片段及其重建信号。图2和图3的顶部面板中显示的信号分别属于发作期和发作间期脑电。在对5个尺度进行小波分解和重构后，在尺度1到5的重构信号分别表示为S1t到S5。如图2和图3所示，尺度3至5上的重建信号在两类EEG之间具有明显的幅度差异。

 B. Feature Extraction

在此基础上，对重构后的信号在尺度3、尺度4和尺度5进行特征提取。为便于后续建立BiGRU神经网络，每个4s的脑电周期被细分为8个5秒得时间切片，对于第j个时间片中的每个EEG通道，分别计算尺度3、4和5上的重构信号的相对能量如下。

这里，1≤j≤8，k的值是3、4或5，这表示小波尺度。Ej(K)是在第j个时间片中的第k尺度上的重构信号s jk的能量，其被给出为

 

其中N是重构信号s_jk的采样点数目，在本工作中N的值为128，因为采样速率为256 Hz，信号s_j_k的长度为0.5秒。

这可以从方程中看出。(1)相对能量值代表信号分量在不同小波尺度上的能量比例。相对能量值在0到1的范围内，对于不同的脑电模式和不同的发作类型，在多分辨率尺度上具有不同的分布。

对于脑电记录中出现癫痫发作的部分，特定小波尺度上的相对能量会上升。对于长度为4s的每段脑电信号，可以得到3×8的特征矩阵。为了产生每个4s EEG时段的特征矩阵，我们根据通道的顺序堆叠计算的相对能量值，例如，如果有23个EEG通道，则特征矩阵将具有69×8的维度。将每个历元的特征矩阵输入到以下基于双向GRU网络的分类模型中。

C. Bidirectional GRU Network

与LSTM网络一样，GRU是为了解决递归神经网络[28]中存在的梯度消失问题而提出的，它通过内部选通机制学习长序列应用中的长期依赖关系。

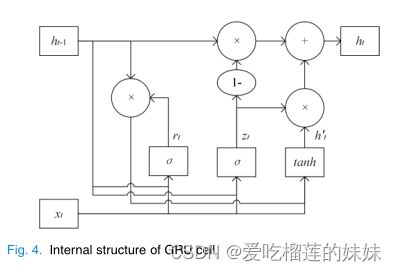
GRU单元具有两个门，即更新门ZT和复位门RT。GRU中门的激活仅取决于当前输入和先前的输出。GRU单元的内部结构如图4所示，其中xt和ht分别是输入向量和时间片t处的隐藏状态，ht是隐藏状态的候选。在时间片t处，时间片t确定需要忘记多少历史信息，并且更新门Zt控制如何使用当前EEG信息来更新隐藏状态。具体公式如下，

 

在上述公式中，σ(·)和Tanh(·)分别为Sigmoid函数和双曲正切函数。符号·和∗分别表示矩阵乘法和哈达玛乘积，[]是两个向量的连接。Wr、Wz和Wh是GRU网络训练要学习的权重矩阵。

在GRU递归神经网络中，信息一般沿着隐含层的GRU单元按时间顺序传播。为了利用癫痫发作的动态演化机制，更好地捕捉脑电信号的长期依赖关系，本文构建了一个基于双向GRU的神经网络模型，其结构如图5所示。

如图5所示，所提出的神经网络模型具有两个隐含层，其中信息分别在正向和反向传播。每个隐层具有8个GRU信元，分别对应8个时间片(T1-T8)。GRU单元的输入Xt是由第t个时间片中的多通道脑电提取的相对能量值组成的矢量，并且隐藏状态输出的维度ht大约是输入长度的两到三倍。然后，将前向和后向两个方向的最后一个GRU的隐藏状态串联并传输到具有一个神经元和S形激活函数的致密(全连接)层中。因此，对于每个4s的脑电周期，获得单个输出变量。

在BiGRU网络训练开始前，如果训练数据集中癫痫脑电信号的持续时间小于非癫痫脑电信号的持续时间，则采用插值法对癫痫脑电信号的特征样本进行上采样，使癫痫发作样本的数量与非癫痫发作样本的数量相等。在本工作中，内插的倍数由非癫痫脑电信号与癫痫脑电信号在训练数据集中的持续时间之比来确定。在bi-GRU网络的训练过程中，选择了ADAM优化算法，并采用二进制交叉熵作为损失函数。迭代次数为300次，批大小设置为128次。作为超参数，本文采用k重交叉验证的方法确定了GRU单元的隐态维，并将k取值为10。

 D. Post-Processing后处理操作

在从脑电记录中检测癫痫发作的过程中，需要对训练好的BiGRU网络的输出进行一系列的后处理，以获得测试脑电信号的类别标签。具体来说，首先对输出序列进行滑动平均滤波，以降低随机噪声，其定义如下：

其中x(I)是BiGRU网络的输出，y(I)表示滤波后的信号。如公式(7)所示，y(I)是包括当前中心点x(I)及其左侧和右侧邻近点的2m+1个点的平均值。2m+1i是一个l s o，称为移动平均滤波器阶。在这项工作中，2m+1的值在5到11的范围内，每个患者的值是不同的，这是由接收器操作特征(ROC)曲线确定的。

然后将滤波后的输出与在BiGRU分类模型的训练阶段确定的阈值进行比较。该阈值对于每个患者是特定的，并且基于训练样本的最小误分类标准来确定。在与所选择的阈值进行比较后，测试样本被标记为癫痫或非癫痫。

最后，考虑到癫痫发作的频率，将短时间间隔内的发作合并为属于同一发作事件。这项工作使用的时间间隔为1至3分钟。

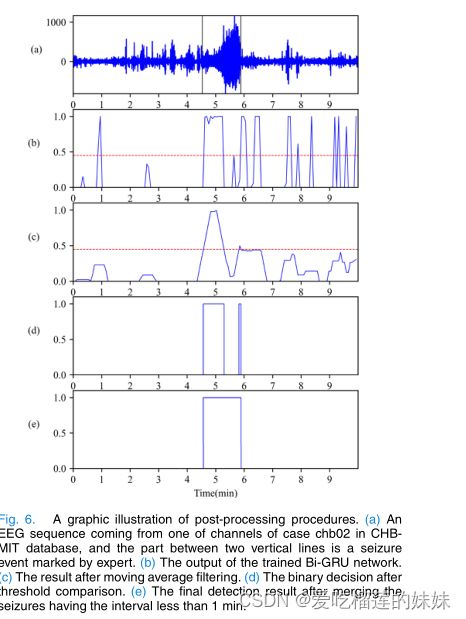
图6说明了使用所提出的癫痫检测方法对CHB-MIT数据库中的多通道脑电序列进行测试时的后处理过程。图6(A)所示脑电来自病例chb02的F4-C4通道，其中两条垂直线之间的部分是临床专家标记的癫痫发作事件。图6(B)给出了来自chb02的经训练的BiGRU网络的输出和序列图6(C)中给出的是移动平均滤波的结果。在图6(C)中，幅度大于以红色虚线表示的阈值的部分被认为是癫痫发作，并在图6(D)中被标记为1。如图6(D)所示，有两个标记为1(癫痫)的部分，它们之间的间隔不到1分钟。然后在图6(E)中合并两个癫痫发作部分，我们认为在当前的脑电记录中检测到一个癫痫发作事件。

 E. Performance Evaluation

为了评估本文提出的癫痫发作检测方法的性能，本文采用了基于分段和基于事件的评估指标。在基于分段的评价中，以检测灵敏度、特异度和准确率作为评价标准，可以通过以下三个公式分别计算。

在上述公式中，Tp(真阳性)和TN(真阴性)分别是指我们的检测系统正确识别的发作和非发作节段的数量。Fp(假阳性)是指被检测系统误判为癫痫的非癫痫EEG节段数，Fn(假阴性)是错误标记的癫痫节段的数目。基于事件的评估方法使用灵敏度和误检率(FDR)作为评估标准。基于事件的灵敏度被用来描述所提出的系统正确检测到的癫痫事件的百分比。对每个病人来说，FDR被定义为在非癫痫发作期间每小时平均错误检测的次数。

IV . RESULTS

所提出的癫痫发作检测方法在配备了2.9 GHz AMD Ryzen 7 4800H处理器的笔记本电脑上运行的MatLab 2016a和TensorFlow 2.1.0上实现，并使用了Python3.7.7。BiGRU网络在训练阶段的运行时间约为14s，1小时多通道脑电的测试时间约为41.8s，其中脑电信号的预处理和特征提取的时间为41.2s。

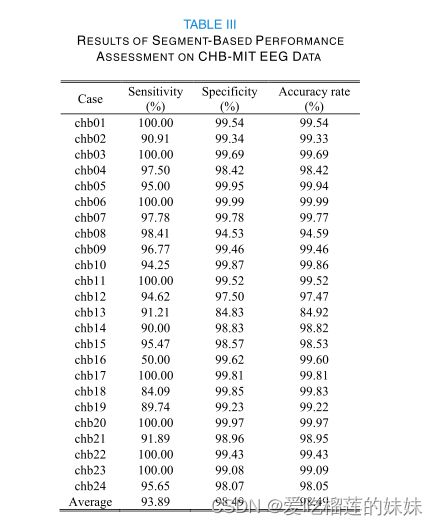
基于CHB-MIT数据库中所有病例的测试数据，对所提出的癫痫检测方法的性能进行了评估。分段式和事件式业绩评估的结果分别列于表三和表四。从表三可以注意到，在基于分段的性能评估中，平均24例获得了93.89%的敏感性和98.49%的特异性。其中8例敏感性为100%，16例特异性和准确率均高于99%。

另一方面，在测试数据集中的128次癫痫发作中，有124次被成功检测，24例的平均灵敏度为95.49，如表IV所示。此外，还有14例的误检率低于每小时0.2次，误检率高的病例主要发生在例4、8、12、14、15、21和23的测试数据上。总体而言，平均误检率为每小时0.31次。

 

表V显示了SH-SDU脑电数据的性能评估结果。前两位患者的敏感度均低于80%，患者1、4的特异度未能达到90%。5例患者平均诊断的敏感性、特异性和准确性分别为87.08%、88.65%和88.55%。此外，在总共29次癫痫发作中，有2次被漏检，平均每小时误检率超过1次。总体结果不如CHB-MIT数据库的结果。原因之一是根据部分患者的临床表现，SH-SDU脑电数据集中存在较多的噪声和伪影。

此外，发作频率高、持续时间短都增加了检测难度，例如患者1在20h左右的测试数据中包含的癫痫发作次数高达16次。

  V. DISCUSSION

A. Characteristics of the Seizure Detection Method癫痫检测方法的特点

本文提出了一种基于双向GRU回归网络的癫痫发作检测方法，并在头皮脑电数据集上进行了测试。在所提出的发作检测方法中，将小波变换作为多通道脑电信号的预处理。在不同的分解尺度上，小波变换具有不同的时频分辨率，克服了短时傅立叶变换(STFT)具有固定时间窗的缺点，适合于奇异信号和非平稳信号的分析。对原始脑电信号进行小波分解后，将3、4、5尺度上的小波系数用于信号重构，由于癫痫发作活动一般集中在3个尺度上的频段，且这些尺度上的癫痫脑电信号与非癫痫脑电信号具有明显的幅值和能量差异，因此，3、4、5尺度上的小波系数具有滤波作用，有助于区分癫痫发作与非癫痫发作的脑电。然而，在癫痫发作的传播和终止阶段，仍然存在一些不在3-5级频率范围内的高频/低频活动，在癫痫发作检测中忽略这些低频活动会产生一些假阴性结果。

在后续的特征提取部分，分别计算重构信号在小波3、4和5尺度上的相对能量。一般来说，当癫痫发作时，脑电表现出有节奏的行为，因此它的大部分能量表现在多分辨率框架的有限尺度上，这与通常分布在大多数小波尺度上的发作间期脑电不同[37]。在特定的小波尺度上存在较高的相对能量值，这表明存在节律性活动，可用于癫痫发作的检测。将重构信号在尺度3、尺度4和尺度5上计算的相对能量值组合成特征矩阵，并输入到BiGRU神经网络。

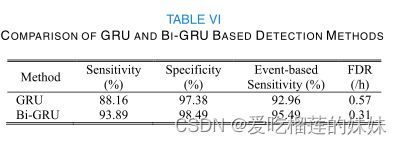
在癫痫发作检测方法中，采用双GRU网络作为分类模型，该模型包括两个隐含层和一个密集输出层。除具有计算代价小、训练速度快、训练样本量少等优点外，本文设计的BiGRU网络通过两层隐含层在正负时间方向传播信息，能够全面捕捉脑电信号序列中的长期相关性。在相同的测试数据集上进行测试时，基于BiGRU网络的癫痫发作检测比基于GRU网络的癫痫发作检测具有更好的检测效果。表六比较了基于GRU和BiGRU的癫痫发作检测方法的检测结果。

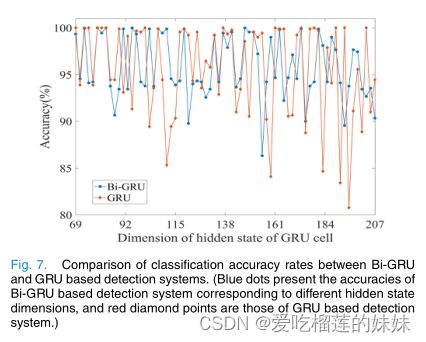
从表六可以看出，基于BiGRU的癫痫发作检测方法获得的基于节段的灵敏度93.89和基于事件的灵敏度95.49都高于基于GRU的方法，这意味着BiGRU对癫痫发作活动具有更好的检测性能。同时，较高的特异度和较低的FDR也表明基于BiGRU的检测方法对脑电模式具有更准确的分类能力。另一方面，当系统参数发生变化时，基于BiGRU的检测方法的性能更加稳定。GRU单元的隐状态维度是影响递归神经网络性能的一个参数，一般没有确定的选取方法。为了证明基于BiGRU的性能稳定性检测系统当隐藏状态维度改变时，我们对CHBMIT数据库中病例chb13的发作间期脑电文件进行了测试。维度在69-207的范围内变化，步长为2。这里的下限等于案例chb13网络中每个GRU小区的输入向量维度，上限设置为下限的三倍。图7显示了GRU网络和BiGRU网络对应不同隐藏状态维度的准确率。在图7中，蓝点表示基于BiGRU的检测系统的准确率值，红色菱形点表示基于GRU的系统的准确率值。显然，当隐含状态维发生变化时，BiGRU的正确率分布更加集中和稳定。

图7.基于BiGRU和GRU的检测系统的分类准确率比较。(蓝点表示基于BiGRU的检测系统对应不同隐藏状态维度的精度，红色钻石点表示基于GRU的检测系统的精度)

总体而言，时频能量分析和基于BiGRU网络的分类模型使该方法在头皮脑电癫痫检测中取得了较好的效果。此外，对BiGRU网络的输出采用了一系列的后处理策略，进一步提高了检测性能。在后处理过程中，为了减少随机噪声和零星波动引起的误检测，采用了滑动平均滤波。然而，移动平均滤波器是一种有限冲激响应(FIR)滤波器，会产生时延，影响基于分段的评估结果。甚至有可能由于移动平均滤波的延迟，那些持续时间较短的发作将被遗漏检测。显然，为了平衡其对检测结果的影响，需要一个合理的滤波顺序。在本工作中，通过绘制ROC曲线来确定滤波阶数。

因为癫痫发作的动力学进展各不相同。

由于不同患者的脑电记录有很大的异质性，不同的患者和癫痫发作，目前的大多数癫痫发作检测方法都是针对不同患者的，通常不能在不同的数据集中对一些患者产生满意的检测结果[38]。本文提出的癫痫发作检测方法也是针对患者的，即建立的检测系统具有患者相关的训练数据集和GRU输出维度和阈值等参数。为了进一步分析所提出的癫痫发作检测方法的性能，本文还进行了与病例无关的验证。从临床应用的角度出发，从不同的案例中选取了检测系统的训练和测试数据。利用CHB-MIT数据库中前5例患者的脑电数据，建立训练数据集，总时长为20.8min。对病例CHB06至CHB24的脑电数据进行了测试，从每个病例中选择了四个脑电文件(至少两个包含癫痫发作的文件)作为测试数据。在总持续时间为75.8h、包含42次癫痫发作的测试数据集上，非案例检测系统的灵敏度为58.25%，特异度为79.97%，准确率为79.79%。

显然，从临床应用的角度来看，非病例验证的结果还有待进一步改进。

B. Analysis of Missed Detections and False Detections对漏检和误检的分析

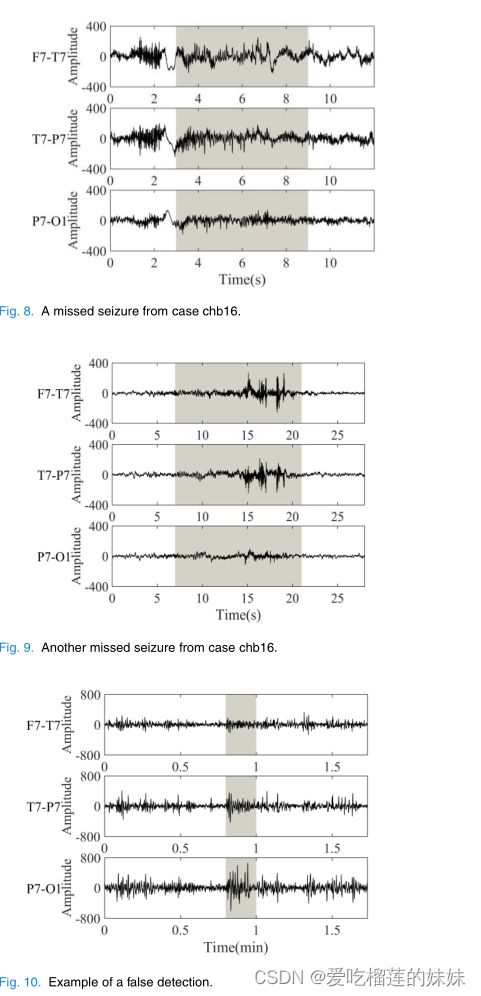
在CHB-MIT数据集上对本文提出的癫痫发作检测方法进行评估时，有4个癫痫发作没有被检测到。遗漏发作分别来自病例chb16、chb18和chb21，漏检可能是由低幅度和不明显的发作活动引起的，例如病例chb18和chb21的发作。此外，癫痫发作持续时间短和后处理中的移动平均滤波也是导致漏检的原因。图8中所示的脑电来自病例chb16的三个通道，包含一次遗漏的癫痫发作，即灰色阴影部分。此癫痫发作事件仅持续6秒。

同样，另一例遗漏发作的病例chb16如图9所示，其中癫痫事件开始和结束部分的EEG呈现低幅度，与非癫痫EEG几乎没有区别，尽管在大约14秒到21秒的短时间内有明显的癫痫发作活动。

另一方面，一些发作间期脑电被检测系统错误地标记为癫痫发作，特别是病例CHB08的脑电文件，其平均FDR高达每小时1.37。发作间期脑电的误检主要是由大量的癫痫样放电和脑电记录中的伪影引起的。作为一个例子，图10说明了chb08的错误检测之一，即灰色阴影部分。可见，T7-P7和P7-O1通道存在明显的大幅度节律活动。

C. Comparison With Other Seizure Detection Methods.与其他癫痫检测方法的比较

表七列出了几种现有的癫痫发作检测方法以供比较，所有这些方法都在CHB-MIT EEG数据库上进行了评估。在Kiranyaz等人的工作中，提出了一种基于集合网络的患者特定分类系统，

在21例146小时的测试数据集上，其平均灵敏度为89.01%，平均特异度为94.71[39]。Zabihi等人。

研究了脑电信号的动态特性，提出了一种基于线性判别的癫痫发作检测方法。