Hector代码原理推导

一、占用栅格地图

顾名思义，栅格就是一个个的网格，由于现实世界是连续的，而计算机只能处理离散的数据因此要将传感器数据进行离散化，还有一个好处是能够节省储存空间和计算时间。

图一 取自《概率机器人》一书的栅格地图

描述一张栅格地图分别需要理解以下几个概念：

• 栅格：可以类比图片的像素点，拥有分辨率、占用率的属性。

• 分辨率：是指一个网格能表示现实世界的距离长短。如：0.05米/每网格，则一个（10米，10米）的点，转移到地图中是（10/0.05，10/0.05）=（20，20）。如果波动范围小于0.05则其都会落在点（**20，20）**中如(10-0.05~10+0.05)/0.05=20（程序中采用向下取整的方式舍掉小数），实现将连续的浮点数进行了离散化。

• 地图的大小：用行网格数目和列网格数目来表示，这里可以适当选择。如：640*480（单位：网格）大小的地图表示，行有640个网格，列有480个网格，如果网格分辨率为0.05米/每网格，则整张地图大小为32*24（单位：米）。

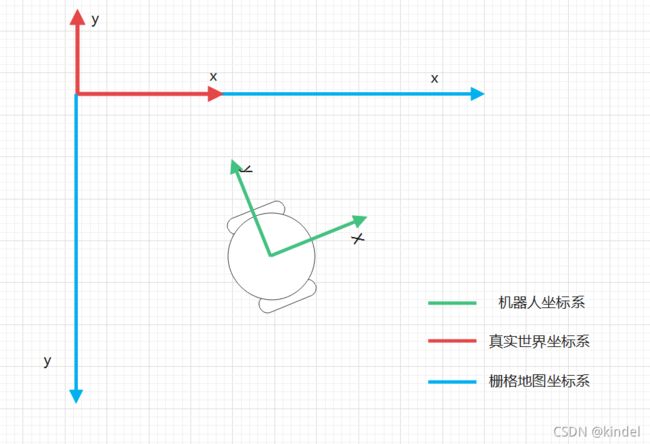
• 地图坐标系与真实世界坐标系：地图坐标系和图片的像素坐标系一致，而真实世界坐标系的方向和机器人本体坐标系的方向一致，如下图：

图二 坐标系之间的关系

可见真实世界坐标系和机器人坐标系的$y$轴都是在$x$轴的左侧，而栅格地图坐标系$y$轴在$x$轴的右侧，是典型的像素坐标系（在视觉slam十四讲相机模型中有讲到相机的坐标）。注意这里世界坐标系和栅格地图坐标系的原点不一定是重合的。
如：在HectorSLAM中采用栅格地图的中点作为真实世界坐标的（0，0）点，这样的好处是，真实距离为负数（-2，-10）的点也能很好的储存在栅格地图中，只需要加上真实世界坐标系相对于栅格地图坐标系的平移就行。

• 占用率：由于无法直接确定某个栅格的占用状态，因此对于每一个栅格我们分别用$p(s=0)$来表示空闲（Free）状态的概率，用$p(s=1)$来表示占用（Occpuied）状态的概率，两者之和为1。用两个值去描述一个网格过于繁杂，因此采用$odd(s)=\frac{p(s=1)}{p(s=0)}$来进行表示。其中的概率会根据观测$z（取0或1）$（即雷达的数据）来更新，$odds(s)$，则更新后的概率我们设置为$odds(s|z)=\frac{p(s=1|z)}{p(s=0|z)}$，这是条件概率的表达形式，根据贝叶斯公式我们会得到：

$$p(s=1|z)=\frac{p(z,s=1)}{p(z)}=\frac{p(z|s=1)\ast p(s=1)}{p(z)}$$$$p(s=0|z)=\frac{p(z,s=0)}{p(z)}=\frac{p(z|s=0)\ast p(s=0)}{p(z)}$$
由此可得：


$$odd(s|z)=\frac{p(z|s=1)\ast p(s=1)/p(z)}{p(z|s=0)\ast p(s=0)/p(z)}=\frac{p(z|s=1)}{p(z|s=0)}\ast \frac{p(s=1)}{p(s=0)}=\frac{p(z|s=1)}{p(z|s=0)}\ast odd(s)$$


为了简便计算将乘法化为加法，进行取对数（可以多积累这种优化计算的方法）:

$$log[odd(s|z)]=log\frac{p(z|s=1)}{p(z|s=0)}+log[odd(s)]$$
由于初始时刻占用与空闲概率应该是等同的，即$p(z=1)=p(z=0)=0.5$，则$logodd(s)=0$，所以着重点就放在了测量模型$log\frac{p(z|s=1)}{p(z|s=0)}$身上，由于$z$只能取0或1，则对应的两种状态我们设置为 $logfree$ ，$logoccu$。
其中:

$$logoccu=log\frac{p(z=1|s=1)}{p(z=1|s=0)}logofree=log\frac{p(z=0|s=1)}{p(z=0|s=0)}$$




这样我们进一步简化符号,用$S^{+}$表示根据观测数据更新后的值,用$S^{-}$表示更新前栅格的概率值:

$$S^{+}=S^{-}+logfree$$ 或者 $$S^{+}=S^{-}+logoccu$$

举个例子:我们假设 $logoccu$= 0.9，$logfree$= -0.7。那么，显而易见，一个栅格状态的数值越大，就越表示该栅格为占据状态，相反数值越小，就表示改栅格为空闲状态。（用概率的方法解决了此前文中提出的激光雷达观测值”不一定准”的问题）。

图三 占用珊格地图建立举例

上图是用两次激光扫描数据更新地图的过程。在结果中，颜色越深越表示栅格是空闲的，颜色越浅越表示是占据的。

二、利用雷达数据建立栅格地图

通过第一节的学习大家对于整个栅格地图有了一定的了解,接下来就是讲解如何使用手中的激光雷达(也不仅仅局限于雷达,其他距离探测器也可以,但就效果来说还是使用主流激光雷达比较合适)来完成整个地图的构建了.
这里我们又多了一个坐标系,雷达坐标系,为了简便我们将其和机器人坐标系进行重合,用机器人坐标系去代替.


图四 雷达点在地图中的表达

如上图所示,我们通过激光雷达可以获得一个边界点(laserpoint,一般来说就是碰到障碍物了)距离我们机器人的距离d,因为我们刚才已经假设了雷达坐标系和机器人坐标系重叠,则laserpoint在机器人坐标系下的表达为:

$$(lase{r}_{{robot}_x},lase{r}_{{robot}_y})=(d\ast cos(angle),d\ast sin(angle))$$

但我们目的是获得laserpoint栅格地图中的表达,由图可得:

$$(lase{r}_{{world}_x},lase{r}_{{world}_y})=(d\ast cos(angle+\theta )+robo{t}_x,-d\ast sin(angle+\theta )+robo{t}_y)$$
$$(robo{t}_x,robo{t}_y为机器人的x,y轴的平移位姿)$$

但是还没有结束,因为d是以米为单位,通过分辨率来转化获得laserpoint在栅格地图中的坐标为

$$(lase{r}_{{world}_x}/分辨率,lase{r}_{{world}_y}/分辨率)$$
就是在栅格地图中的网格坐标$(cel{l}_x,cel{l}_y)$了.

在我们完成对障碍物在地图位置的确认之后我们可以进行地图构建了.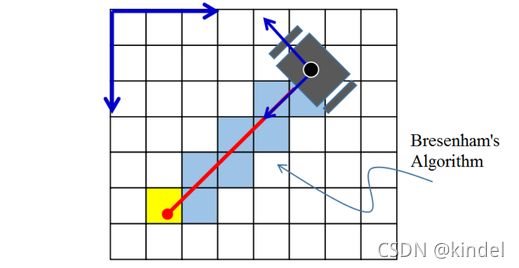


图五 bresenham直线算法

如上图，我们设定laserpoint为末端坐标，机器人本体为起点坐标，就可以做一条直线，在达到laserpoint之前的各个网格都是空闲的，末端则是占用的，但是如何确定直线所经过的网格点呢，我们这里使用bresenham直线算法来实现（后面会再进行详细的讲解），当确定了网格点之后我们可以根据前文的公式对网格点进行状态更新，对于途经的点使用$S^{+}=S^{-}+logfree$进行更新，对于终点用$S^{+}=S^{-}+logoccu$进行更新。这里我们使用的是概率更新公式，允许一定程度的误判，也提供了继续更新修改的机会，这样我们的栅格地图就一步一步构建好了。

三、HectorSLAM的原理讲解

通过上面所学相信你对于占用珊格地图有一定的了解，以及利用手中的二为雷达建立一个简单的珊格地图，但是在实际建图过程中，雷达不可能是固定不动的，不然建出来的图原点一直是固定的则会发生错误，如上面已经固定了地图原点建出来的图，如果你尝试去移动或旋转（更为明显）它，会发现有很多地图重叠的部分，这是产生了误匹配。一般建图要同时知道雷达自身在地图中的位置，这样利用坐标变换等工具把障碍物在地图中的位置求出来，进而就能够构建一个完整的地图了。这里获得自身位置的方法有很多，如利用简单平地小车的轮式里程计、GPS+惯导，甚至是最简单的沿着直线行走具有超声波模块的小车（如当你指定墙的一点，则小车垂直于这一点进行前进，能够通过超声波测距来完成小车的定位，虽然没有什么实际用途，但是发挥想象力，只要能完成定位就行），完成定位就相当于获得了图四中的$(robo{t}_x,robo{t}_y)$和机器人相对于珊格地图的转角$theta$，这样通过坐标变化就能实时知道当前位置，完成地图的构建和更新了。而HectorSLAM则是一个能直接用雷达同时完成定位和建图两大工作的经典SLAM算法，因此在HectorSLAM中这两部分相互影响，更为紧密。

1.定位

定位要完成的事情就是得到$\xi =(robo{t}_x,robo{t}_y,theta)$三个重要的数值，同时要尽量准确，而HectorSLAM定位通过scan_to_map的方式来进行的，也就是通过雷达数据与当前地图的一个匹配来完成，因为除了这两个重要的东西我们也没有别的什么可以依赖了。通过利用激光雷达数据的高速特性（我相信光的速度），一般获得数据都是在人反应时间之内的，且雷达自身转速基本都达到10Hz(但建图时角速度还是不能太快，会出现畸变现象，有时间再进行解答)，10Hz也就是一圈0.1s的时间，如果在这0.1s里产生的旋转和位移不会太大，则障碍物还是能够匹配上，这样就可以完成这微小位姿的计算了，但一般现实中位姿是连续的，但地图是离散的，这时候我们就用到双线性插值的算法(不要畏惧数学，那是你变强的必经之路，而且仔细去看你会发现就是初中的数学知识换了身衣服)。
既然我说了是初中的知识，那我们就从初中的知识进行说起，先讲讲单线性插值。

• 单线性插值

图六 单线性插值

根据初中的两点法可以列出方程$$\frac{y-y_1}{x-x_1}=\frac{y_2-y}{x_2-x}$$然后对其进行移向得到$$y=\frac{x_2-x}{x_2-x_1}\ast y_1+\frac{x-x_1}{x_2-x_1}\ast y_2$$其中$y_1$和$y_2$前面的那个分式可以看作是他们的权重，你会发现，当$x$更靠近$x_1$时,$y_1$的权重越大,反之亦然。

另一种理解方式可以从相似三角形出发$$\frac{y-y_1}{x-x_1}=\frac{y_2-y_1}{x_2-x_1}$$也可以推出上面的式子(怎么感觉在讲线性方程一样呢?).这里的y我们可以换成另一种指标,而它是和当前点的坐标$(x,y)$有关的,设为$f(P)$,则根据权重占比得到：
$$f(P)=\frac{x_2-x}{x_2-x_1}\ast f(P_1)+\frac{x-x_1}{x_2-x_1}\ast f(P_2)$$
这就完成了单线性插值的讲解。
说明：如果进一步去理解的话,$f(P)$可以当作是一个与$x$有线性关系,而与$y$有非线性关系的函数,这里就用可以用$x$来描述权重,$f(P)$来指定关于$y$的非线性表达.

• 双线性插值

讲完单线性插值后应该发现确实不难,只是换了个唬人的名字罢了,趁热继续讲解学习双线性插值.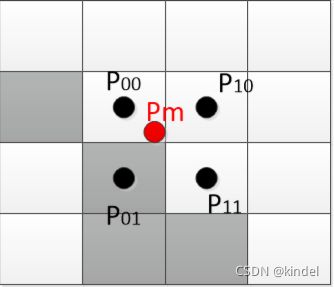

（a）


（b） （c）
图七 双线性插值-截取自原HectorSLAM论文

首先看图(a),随意取一个雷达点$P_m$,由于在真实世界中数据是连续的,它很难准确的落到某个珊格中,同时我们也允许数据会稍微带一点误差,为了增大容错率,我们取离其最近的几个珊格点坐标$P_{00},P_{10},P_{01},P_{11}$,并用他们的占用率来估计$P_m$点的占用率$M(P_m)$,接下来就是运用线性插值的时候了.

如图(b)，首先求得x轴的权重分配,得到:
$$M(I_0)=\frac{x_1-x}{x_1-x_0}\ast M(P_{00})+\frac{x-x_0}{x_1-x_0}\ast M(P_{10})$$
$$M(I_1)=\frac{x_1-x}{x_1-x_0}\ast M(P_{01})+\frac{x-x_0}{x_1-x_0}\ast M(P_{11})$$
再在y轴进行一次权重分配可以得到:
$$M(P_m)=\frac{y_1-y}{y_1-y_0}\ast M(I_0)+\frac{y-y_0}{y_1-y_0}\ast M(I_1)$$
最后可以得到:

$$M(P_m)=\frac{y_1-y}{y_1-y_0}(\frac{x_1-x}{x_1-x_0}\ast M(P_{00})+\frac{x-x_0}{x_1-x_0}\ast M(P_{10}))+\frac{y-y_0}{y_1-y_0}(\frac{x_1-x}{x_1-x_0}\ast M(P_{01})+\frac{x-x_0}{x_1-x_0}\ast M(P_{11}))$$

同时通过上面可以知道坐标是邻接的$$x_0+1=x_1,y_0+1=y_1$$最终化简可知分母全为1可

$$M(P_m)=(y_1-y)((x_1-x)\ast M(P_{00})+(x-x_0)\ast M(P_{10}))+(y-y_0)((x_1-x)\ast M(P_{01})+(x-x_0)\ast M(P_{11}))$$


事到如今，我们已经学会了如何从一个点附近的四个点来求得我们的点的占用率$M(P_m)$了，但是这和我们之前的定位有什么关系呢，我们可是要求解$\xi =(robo{t}_x,robo{t}_y,\theta )$呀，说到这里小伙伴们就应该回忆起我们的$P_m$是怎么来的了，靠的不就是$\xi$吗，所以这里我们可以知道$P_m$是关于$\xi$的一个函数，我们设为$S(\xi )$,则


$$S(\xi )=\left(\begin{array}{cc}cos\theta & -sin\theta \\ sin\theta & cos\theta \end{array}\right)\left(\begin{array}{c}{P}_{m_x}\\ P_{m_y}\end{array}\right)+\left(\begin{array}{c}robo{t}_x\\ robo{t}_y\end{array}\right)$$
然后呢？

其实我们要求的不单单是$\xi$,而是要求最优的$\xi$，我们称之为${\xi }^{\ast }$,有的小伙伴会说，啊博主你这不是废话吗？是但不完全是，如何能求最优，那起码有条件或者前提吧,那应该是什么呢？远在天边近在眼前，就是我们的雷达，雷达扫到的点是不是障碍物？是！那障碍物有什么特点？占用率为1，那我们千辛万苦算得$M(P_m)$就派上用场了，只要让其无限趋近于1不就行了吗？再进一步就是让$M(S(\xi ))$接近于1，$${\xi }^{\ast }=argmin\sum _i^n[1-M(S(\xi {)}_i){]}^2$$ , 没学过最小二乘法的小伙伴也不用担心，只要理解成$$\sum _i^n[1-M(S(\xi {)}_i){]}^2->0$$趋近于0就行。

一般求解最小二乘法就是求导迭代的方法，但是这样在高维度空间(什么是高维度空间，就是在常见的三维以上的空间计算量较大，因此我们采用高斯牛顿法(如图八，是《视觉SLAM十四讲的》的内容)进行求解。






图八 高斯牛顿法


根据以上方法我们也用$\Delta \xi$来表示变化量，再进行泰勒展开，得到:

$${\xi }^{\ast }=argmin\sum _i^n[1-M(S(\xi +\Delta \xi {)}_i){]}^2=argmin\sum _i^n[1-M(S(\xi {)}_i)-\nabla M(S(\xi {)}_i)\frac{\partial S(\xi {)}_i}{\partial \xi }\Delta \xi {]}^2$$

对$\Delta \xi$进行求导且令倒数为0得到:

$$\sum _i^n(-2\nabla M(S(\xi {)}_i)\frac{\partial S(\xi {)}_i}{\partial \xi }[1-M(S(\xi {)}_i-\nabla M(S(\xi {)}_i)\frac{\partial S(\xi {)}_i}{\partial \xi }\Delta \xi ])=0$$

令$f(\xi )=1-M(S(\xi )),J(\xi )=\nabla M(S(\xi ))\frac{\partial S(\xi )}{\partial \xi }$，这里我们就省略累加了，代入化简得到:
$$J(\xi {)}^{T}J(\xi )\Delta \xi =-J(\xi )f(x)$$

形如图片中式子:

这样只要我们求出$$f(\xi )=1-M(S(\xi )),J(\xi )=\nabla M(S(\xi ))\frac{\partial S(\xi )}{\partial \xi }$$就能完成计算啦。

• 1. 对于$f(\xi )$的结果是显而易见的，因为刚才我们已经求出了$M(S(\xi ))=M(P_m)$

• 2. 对于$J(\xi )=\nabla M(S(\xi ))\frac{\partial S(\xi )}{\partial \xi }$,首先我们求取$\nabla M(S(\xi ))=\nabla M(P_m)=(\frac{\partial M}{\partial x},\frac{\partial M}{\partial y}{)}^T$,
     由

$$M(P_m)=(y_1-y)((x_1-x)\ast M(P_{00})+(x-x_0)\ast M(P_{10}))+(y-y_0)((x_1-x)\ast M(P_{01})+(x-x_0)\ast M(P_{11}))$$


得到:
$$\frac{\partial M}{\partial x}=(y_1-y)(-M(P_{00})+M(P_{10}))+(y-y_0)(-M(P_{01})+M(P_{11}))$$

$$\frac{\partial M}{\partial y}=-((x_1-x)\ast M(P_{00})+(x-x_0)\ast M(P_{10}))+((x_1-x)\ast M(P_{01})+(x-x_0)\ast M(P_{11}))$$


然后计算 $\frac{\partial S(\xi )}{\partial \xi }$:
由$$S(\xi )=\left(\begin{array}{cc}cos\theta & -sin\theta \\ sin\theta & cos\theta \end{array}\right)\left(\begin{array}{c}{P}_{m_x}\\ P_{m_y}\end{array}\right)+\left(\begin{array}{c}robo{t}_x\\ robo{t}_y\end{array}\right)$$

得到:
$$\frac{\partial S(\xi )}{\partial \xi }=\left(\frac{\partial S(\xi )}{\partial robo{t}_x},\frac{\partial S(\xi )}{\partial robo{t}_y},\frac{\partial S(\xi )}{\partial robo{t}_z}\right)=\left(\begin{array}{ccc}1& 0& -sin\theta P_{m_x}-cos\theta P_{m_y}\\ 0& 1& cos\theta P_{m_x}-sin\theta P_{m_y}\end{array}\right)$$

这样就可以通过$J(\xi {)}^{T}J(\xi )\Delta \xi =-J(\xi )f(x)$，算出$\Delta \xi$,最后得到最新位置:
$${\xi }^{+}={\xi }^{-}+\Delta x$$

完成定位！

2.建图

HectorSLAM的建图方式和我们上面所说的占用栅格地图的建立其实大同小异，多了一个多分辨率地图的概念，同时我们会详细讲解实现地图更新的bresenham直线算法。

• 多分辨率地图

HectorSLAM中有一个多分辨率地图的概念，按简单来说就是地图的大小会进行放缩，一般缩放比例系数为0.5,同时分辨率也会有所放缩，地图越小，分辨率越差，学过图像金字塔的同学可能比较清除，这里我们就举一个例子：


图九 多分辨率地图


如图九所示，如果我们设置地图层数为3层时，则会产生三个分辨率的地图，对于0层来说是我们所输入的最高分辨率的一张图。当缩放比例为0.5时，每增加一层，地图的大小都会缩小一半，同时分辨率也会变为原来的两倍，因为地图变小了所以网格变小了，但是现实中的距离是不变的，那只能是将原本0.05m/cell的四个网格的东西放到一个0.1m/cell网格里去了。该规则会用在我们处理雷达数据的时候，如一个laserpoint坐标为（2m,2m）在0层地图的坐标就是（40，40），在1层就是（20，20），然后再分配到对应地图去处理。


这样的作用是什么呢？在HectorSLAM中计算位姿时是从最高层往下来迭代计算的，好处是分辨率越大，一个点允许的波动越大，如最高层允许的波动为0.2m，这样我们就更有机会去匹配上，当我们完成粗匹配后，再利用粗位姿和高分辨率雷达数据进行细化，最后细化到0.05m的波动下，位姿就更加准确了。

• 建图过程

前面的一切好像都是在为定位而服务的，这也是为什么我说定位和建图是相辅相成的原因，尤其是对于HectorSLAM这个只使用雷达数据完成定位和建图的算法两者更为紧密。现在我们来详细讲解一下建图的过程：

• 1.获得某一帧的雷达数据laserpoints

• 2.与当前地图数据进行匹配，获得定位位姿$\xi$

• 3.判断位姿的位移变化或角度变化是否大于阈值，二者满足其一就可，若大于则进行地图更新

• 3.通过位姿$\xi$来修正laserpoints在地图中的位置

• 4.取laserpoints中的一个laserpoint，循环

  • 1.以当前机器人在地图中的坐标$(robo{t}_x/分辨率,robo{t}_y/分辨率)$为起点，laserpoint在地图中的坐标$(lase{r}_{{world}_x}/分辨率,lase{r}_{{world}_y}/分辨率)$为终点。
  • 2.利用bresenham直线算法确定起点到终点这条激光射线经过的坐标，为什么不能直接就确定呢，因为地图是栅格化，是离散的，因此要确定哪个栅格属于这条直线，到bresenham直线算法讲解的时候可能更加清晰。
  • 3.利用构建占用栅格地图的算法进行占用率更新：$$S^{+}=S^{-}+logfree或者S^{+}=S^{-}+logoccu$$

• 5.这样我们就可以通过地图的占用率来确定是否被占用了，在HectorSLAM判断占用的阀值是 >0 表示被占用，<0 表示空闲，通过多次迭代更新，地图的占用率将会更加准确，进而促进了定位的准确。

• bresenham直线算法

其实这个算法理解了之后也是初中级别的，但是网上的说明方法都不一样，会让人一下子摸不着头脑，这里采用一种简单的方式，然后到算法讲解那块会借助同样的思路去分析，但是有点不一样。
首先我们视野放在第一象限，因为四个象限是对称所以随便选择一个象限能使用，则对应都能使用。在第一象限中的直线我们分别有两种情况，一种是斜率>1，另一种是斜率<1，其实这两种也是对称的，只是把x和y的位置进行交换就行，那我们就拿斜率<1的情况来解释。


图十 Bresenham直线算法


我们知道起点$beginpoint(x_0,y_0)$就是我们的机器人本体坐标，终点$endpoint(x_1,y_1)$就是我们laserpoint的坐标，我们知道能通过两点式来获得一个一个直线方程:


$$\frac{y-y_0}{y_1-y_0}=\frac{x-x_0}{x_1-x_0}$$ 可化为 $$(y_1-y_0)(x-x_0)-(x_1-x_0)(y-y_0)=0$$
令$dy=(y_1-y_0)，dx=(x_1-x_0)$,得：

$$f(x,y)=\Delta y(x-x_0)-\Delta x(y-y_0)=0$$
其中我们得目的就是去确定从beginpoint到endpoint这条直线上的栅格点在什么位置，小伙伴们会说，这不是一眼就看出来了吗？确实在我们人眼一看就知道那个方块应该在直线上，但是计算机无法理解，也正是这样创造了计算机视觉，跑题了。实际上我们确定一个点无非是确定它是$(x+1,y)$，还是$(x+1,y+1)$呗，因为我们已经规定了斜率<1。
当我们从$(x_0,y_0)$出发，首先判断$x_0+1$的$y$值，可见很容易我们就判断直线落在1方格，同时也很容易就确定了2，3方格，但是到4，5时候则需要一点眼力，但还是能看出来直线偏上多一点，为什么呢？因为有中点这个这个衡量标准，如中点$x_3+1,y_3+0.5$，如果中点落在直线的下方对应代入到方程中得到$f(x,y)>0$，那就直线大部分会落在$x_3+1,y_3+1$，反之$f(x,y)<0$则取下一个方格为$x_3+1,y_3+1$。

现在我们知道了判断公式，就可以进行循环迭代完成更新了，步骤如下：

• 确定$f(x_0+1,y_0+0.5)=f(x_0,y_0)+\Delta y-0.5\Delta x$ 是 >0 或者 <0
• $x_1=x_0+1$ ; 若大于0，则$y_1=y_0$,若<0,则$y_1=y_0$
• 这样再通过计算$f(x_1+1,y_1+0.5)$的值就可以完成所有的方格的迭代了，其实这里有个计算小技巧：

因为$x+1$代表$f(x,y)+\Delta y$, $y+1$代表$f(x,y)-\Delta x$,因此只要确定了下一个方格的位置，就可以用上一个方格来计算得到其值，如$$f(x_1,y_1)=f(x_0+1,y_0+1)=f(x_0,y_0)+\Delta y-\Delta x$$, 然后就可以继续计算$f(x_1+1,y_1+0.5)$来确定$x_2,y_2$啦。


到这里建图就完成了。

---

参考链接

https://www.cnblogs.com/qsm2020/p/14172105.html
https://www.cnblogs.com/cyberniklee/p/8484104.html
https://www.cnblogs.com/dlutjwh/p/10962026.html
https://blog.csdn.net/u012343179/article/details/78590102
https://zhuanlan.zhihu.com/p/349253807
https://zhuanlan.zhihu.com/p/265221559