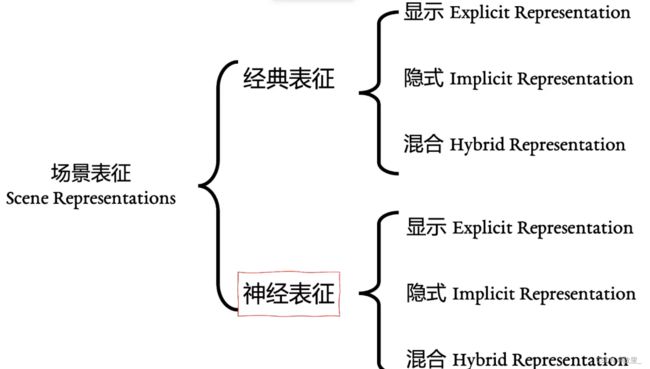
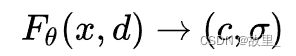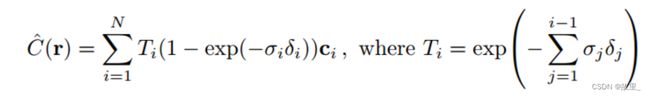读论文-NeRF学习笔记

NeRF的背景

经典场景特征与神经表征


neRF属于神经表征的隐式表征

NeRF的原理

NeRF主要功能： 使用静态场景下的多个视角的照片（大约几十至上百张），合成出任意新视角的图片。

NeRF的算法思路：

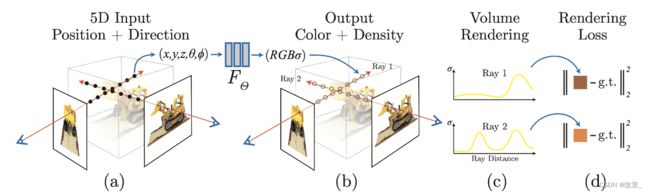
Step1 ：使用MLP学习该场景的隐式3D模型表达

MLP模型示意图。输入一个3d点x和观测方向d的高频编码向量，网络预测该点的密度sigma和颜色c

Step 2:使用体渲染方程将3D场景渲染成图片

图形上的点 P(u,v,1) , 他的像素值 rgb 可以通过对该点P发出的射线上的所有的点 的 c 和体密度 进行积分得到。

Step 3：训练

训练集是几十张或者几百张该场景不同相机位姿拍摄的图片
首先使用SFM算法求出所有图片的相机相对世界坐标系的位姿 （R,t）
每张图片的每个像素点都是一个训练样本 (u,v) → rgb
以像素点（u，v）为例：
从该点发出的射线在世界坐标系中的表示为

起始点 [公式] 的世界坐标也同样可以有相机的内外参求得
然后在该射线上采样n个采样点。
使用MLP预测这n个点的体密度，和c ,然后使用体渲染方程的离散公式算出该像素点的预测值 rgb。
然后计算预测的颜色值和真实颜色值的L2距离作为loss进行监督训练。

Step 4： 观测方向d的作用：

一个点的密度密度智能是该点位置x的函数。
但该点的颜色还取决于观测方向（我们观看空间中一个物体的某个点，从光源照射方向观看和从阴影方向观看，它的亮度是不一样的。）

Step 5：Positional encoding

直接让MLP学习映射很难，将x，d 编码危机高维向量后学习会更加容易。
因此使用如下高频函数进行编码。

step 6：多层级采样策略

均匀采样方式采样射线上64个点
这64点的密度值估计出密度分布函数。
再使用逆采样算法集中对高密度的区域采样128点。
使用该策略可以提高采样的效率，不需要对射线上所有区域都进行密集的采样。

Neural Radiance Field Scene Representation（NeRF场景表示）
1.首先将连续的场景隐式地用一个函数表示，该函数的输入是一个5D向量（3D的位置坐标x = ( x , y , z ) 以及2D视角方向( θ , ϕ )，其中我们将视角方向用一个三维笛卡尔单位向量d \textbf{d}d来表示；输出为颜色信息c \textbf{c}c=(r,g,b)和体密度σ——有关于x点处的体密度，σ(x)被定义为一条射线r在经过x处的一个无穷小的粒子时被终止的概率，类似于x点处的不透明度 。在NeRF下，该函数近似用MLP网络不断优化来实现，记作：F Θ : ( x , d ) → ( c , σ )
2.接下来将从MLP网络中得到的体密度和颜色信息利用体绘制（volume rendering）方法合成到图像中去；
3.最后通过最小化体绘制合成图像与真实图像之间的Loss函数来优化MLP网络的参数，得到隐式场景表示；

Volume Rendering with Radiance Fields（基于辐射场的体绘制方法）

方法介绍

体绘制（Volume rendering）是一种用于显示离散三维采样数据集的二维投影技术，为了渲染三维数据集的二维投影，首先需要定义相机相对于几何体的空间位置，还需要定义每个点即体素的不透明性以及颜色；


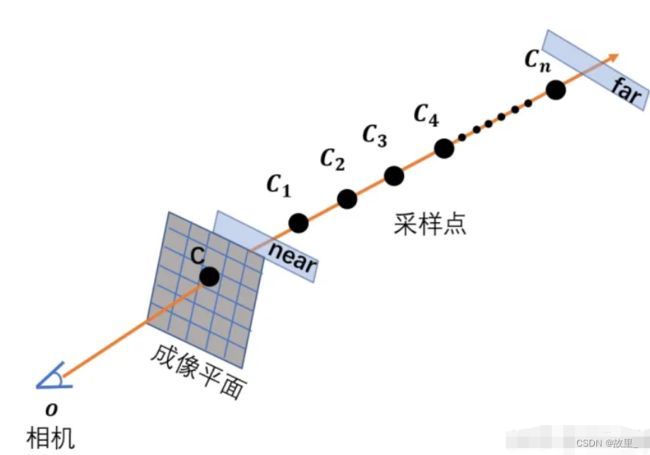
1.由相机 o （相机光心）和某个成像点 C 两点确定的射线如图所示。

2.以相机为原点 ，射线方向为坐标轴方向建立坐标轴。

3.则坐标轴上任意一点坐标可表示为o + t d 。其中t 为该点到原点距离， d 为单位方向向量。near，far 实际上是两个垂直于射线，平行于成像平面的平面。

4.在这里，也用near、far表示那两个平面与射线的交点。在射线上采样的范围是从 near 点到 far 点。理论上，如果对于相关的 scene 我们一无所知，near 点应该被设在在原点（相机处），far 点则在 无穷远。

5.但是实际上如果我们要处理的是 synthetic dataset，则会根据已知的物体在 scene 中的范围调整 near 和 far。因为这样可以减少计算量。 将 near 到 far 的范围 n 等分，在第 i个等分小区间内均匀随机采样，得到采样点点Ci 。注意，用大写的Ci 代表第 i个采样点。而小写的ci 代表它的RGB颜色向量。

Optimizing a Neural Radiance Field（优化神经辐射场）

技巧1——Positional encoding（位置编码）

NeRF成功的因素，除了文章本身的 idea 外，即训练一个 MLP ：

其中，x,d 分别代表 scene 中的任意一个三维坐标和单位方向向量。 C σ分别代表由三维坐标和方向向量唯一确定的相机射线确定的三维坐标处的颜色，和三维坐标处的 Volume Density。 还包括一个非常重要的 trick：Positional Encoding。图2展示了 NeRF论文中的实验结果对比。在图2中用红色矩形框标注出来的就是没有使用 Positional Encoding 的结果，它明显比使用了的（Complete Model）结果差。差的部分主要体现在图像的一些 high-frequency 部分。

那么，为什么说Positional Encoding 至关重要呢？ 为了回答这个问题，首先要介绍一下关于“图像”的一个概念：high-frequency （高频）和 low-frequency（低频）。如图4所示，标号1所处的地方是白色类似于桌布的东西，标号2所处的地方是核桃。在前者的小区域内，移动一点位置，颜色并不会变化很大，但是后者就会。前者的区域对应 low-frequency，后者的区域对应 high-frequency

公式中的 在下文中会解释其含义。 图 中下半部分使用了 Positional Encoding： x先经由γ(x) 处理，然后将处理后的中间量输入进 F Θ

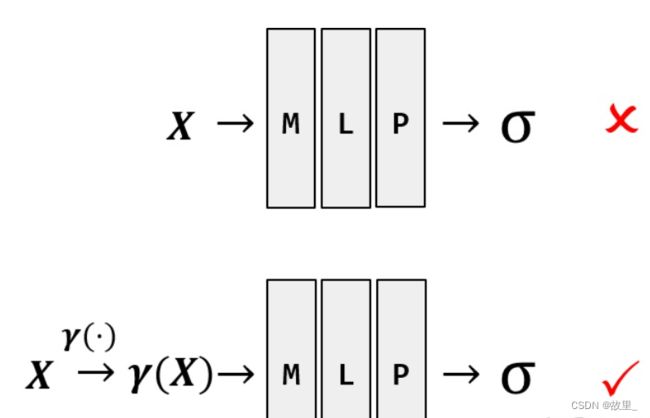
深度神经网络偏向于学习图像 low-frequency 的部分，而针对 high-frequency 的部分难以学习，而对输入施加如公式所示的 Positional Encoding 后，则能将 input 映射到高维空间从而解决这个问题。 公式中 的值决定了神经网络能学习到的最高频率的大小。

如果L  的值太小，则会导致 high-frequency 区域难以重现的问题。
如果 L 的值太大，则会导致重现出来的图像有很多噪声的情况。
NeRF 的作者根据实验结果，发现关于三维点坐标  x和 单位方向向量 d ， L 分别取 10 与 4 的情况，实验效果比较好。

NeRF 位置编码代码分析

def get_embedder(multires, i=0):

    if i == -1:
        return nn.Identity(), 3
    
    embed_kwargs = {
                'include_input' : True,  # 如果为真，最终的编码结果包含原始坐标
                'input_dims' : 3,  # 输入给编码器的数据的维度
                'max_freq_log2' : multires-1,
                'num_freqs' : multires,  # 即论文中 5.1 节位置编码公式中的 L 
                'log_sampling' : True,
                'periodic_fns' : [torch.sin, torch.cos],
    }
    
    embedder_obj = Embedder(**embed_kwargs)
    embed = lambda x, eo=embedder_obj : eo.embed(x)  # embed 现在相当于一个编码器，具体的编码公式与论文中的一致。
    return embed, embedder_obj.out_dim

class Embedder:
    def __init__(self, **kwargs):
        self.kwargs = kwargs
        self.create_embedding_fn()
        
    def create_embedding_fn(self):
        embed_fns = []
        d = self.kwargs['input_dims']
        out_dim = 0
        
        # 如果包含原始位置
        if self.kwargs['include_input']:
            embed_fns.append(lambda x : x)  # 把一个不对数据做出改变的匿名函数添加到列表中
            out_dim += d
            
        max_freq = self.kwargs['max_freq_log2']
        N_freqs = self.kwargs['num_freqs']
        
        if self.kwargs['log_sampling']:
            freq_bands = 2.**torch.linspace(0., max_freq, steps=N_freqs)  # 得到 [2^0, 2^1, ... ,2^(L-1)] 参考论文 5.1 中的公式
        else:
            freq_bands = torch.linspace(2.**0., 2.**max_freq, steps=N_freqs)  # 得到 [2^0, 2^(L-1)] 的等差数列，列表中有 L 个元素
            
        for freq in freq_bands:
            for p_fn in self.kwargs['periodic_fns']:
                embed_fns.append(lambda x, p_fn=p_fn, freq=freq : p_fn(x * freq))  # sin(x * 2^n)  参考位置编码公式
                out_dim += d  # 每使用子编码公式一次就要把输出维度加 3，因为每个待编码的位置维度是 3
                    
        self.embed_fns = embed_fns  # 相当于是一个编码公式列表
        self.out_dim = out_dim
        
    def embed(self, inputs):
    # 对各个输入进行编码，给定一个输入，使用编码列表中的公式分别对他编码
        return torch.cat([fn(inputs) for fn in self.embed_fns], -1)

技巧2——Hierarchical volume sampling（多层级体素采样）