NNDL实验5

深入研究鸢尾花数据集

画出数据集中150个数据的前两个特征的散点分布图：
这里是借用的代码：
只使用了前两个标签的数据

df = pd.read_csv('Iris.csv', usecols=[1, 2, 3, 4, 5])
"""绘制训练集基本散点图，便于人工分析，观察数据集的线性可分性"""
# 表示绘制图形的画板尺寸为8*5
plt.figure(figsize=(8, 5))
# 散点图的x坐标、y坐标、标签
plt.scatter(df[:50]['SepalLengthCm'], df[:50]['SepalWidthCm'], label='Iris-setosa')
plt.scatter(df[50:100]['SepalLengthCm'], df[50:100]['SepalWidthCm'], label='Iris-versicolor')
plt.scatter(df[100:150]['SepalLengthCm'], df[100:150]['SepalWidthCm'], label='Iris-virginica')
plt.xlabel('SepalLengthCm')
plt.ylabel('SepalWidthCm')
# 添加标题 '鸢尾花萼片的长度与宽度的散点分布'
plt.title('Scattered distribution of length and width of iris sepals.')
# 显示标签
plt.legend()
plt.show()

4.5 实践：基于前馈神经网络完成鸢尾花分类

继续使用第三章中的鸢尾花分类任务，将Softmax分类器替换为前馈神经网络。
损失函数：交叉熵损失；
优化器：随机梯度下降法；
评价指标：准确率。

import torch
import pandas as pd
import numpy as np
import torch.nn as nn
import matplotlib.pyplot as plt
import torch.nn.functional as F
from torch.autograd import Variable
import matplotlib.pyplot as plt
from torch.nn.init import constant_, normal_, uniform_
import copy
from torch.utils.data import DataLoader as loader
#数据集：
df = pd.read_csv('Iris.csv', usecols=[1, 2, 3, 4, 5])

# pandas打印表格信息
# print(df.info())

# pandas查看数据集的头5条记录
# print(df.head())

"""绘制训练集基本散点图，便于人工分析，观察数据集的线性可分性"""
# 表示绘制图形的画板尺寸为8*5
plt.figure(figsize=(8, 5))
# 散点图的x坐标、y坐标、标签
plt.scatter(df[:50]['SepalLengthCm'], df[:50]['SepalWidthCm'], label='Iris-setosa')
plt.scatter(df[50:100]['SepalLengthCm'], df[50:100]['SepalWidthCm'], label='Iris-versicolor')
plt.scatter(df[100:150]['SepalLengthCm'], df[100:150]['SepalWidthCm'], label='Iris-virginica')
plt.xlabel('SepalLengthCm')
plt.ylabel('SepalWidthCm')
# 添加标题 '鸢尾花萼片的长度与宽度的散点分布'
plt.title('Scattered distribution of length and width of iris sepals.')
# 显示标签
plt.legend()
plt.show()

# 取前100条数据中的：前2个特征+标签，便于训练
data = np.array(df.loc[0:150])
# 数据类型转换，为了后面的数学计算
X, y = data[:, :-1], data[:, -1]
name=['Iris-setosa','Iris-versicolor','Iris-virginica']

def choose2(a):
    name = ['Iris-setosa', 'Iris-versicolor', 'Iris-virginica']
    nl = len(name)
    re_list=[]
    for i in a:
        re_list.append(name.index(i))
    return re_list

hot=choose2(y)
y = np.array(hot,dtype='float32')
X = np.array(X,dtype='float32')
X=torch.tensor(X)
y=torch.tensor(y).type(torch.LongTensor)#设成long要不然softmax报错
banch_size=50
x_loader = loader(dataset=X,batch_size=banch_size)
y_loader = loader(dataset=y,batch_size=banch_size)


class Net(torch.nn.Module):
    def __init__(self, n_feature, n_hidden, n_output,mean_init=0.0, std_init=0.3, b_init=0.1):
        super(Net, self).__init__()
        self.hidden = torch.nn.Linear(n_feature, n_hidden)
        normal_(tensor=self.hidden.weight, mean=mean_init, std=std_init)
        constant_(tensor=self.hidden.bias, val=b_init)
        self.out = torch.nn.Linear(n_hidden, n_output)

    def forward(self, x):
        x = F.sigmoid(self.hidden(x))
        x = self.out(x)
        return x
#4,6,3
net = Net(n_feature=4, n_hidden=6, n_output=3)
#打印网络初始化的参数和网络结构
for name, parms in net.named_parameters():
    print('-->name:', name, ' -->grad_value:', parms.grad)
print(net)

#优化器和损失函数
optimizer = torch.optim.Adam(net.parameters(), lr=0.01, betas=(0.9, 0.99))
loss_func = torch.nn.CrossEntropyLoss()
#训练
ac_list=[]
for t in range(500):

    for name, parms in net.named_parameters():
        print('-->name:', name, ' -->grad_value:', parms.grad)
   #print('输入：',X)
    for x_mbgd,y_mbgd in zip(x_loader, y_loader):
        out = net.forward(x_mbgd)
        #print(out.shape, y.shape)
        loss = loss_func(out, y_mbgd)
        optimizer.zero_grad()
        loss.backward()
        optimizer.step()
    if t % 1 == 0 :
        _, prediction = torch.max(F.softmax(net.forward(X)), 1)
        #print('输出：',prediction)
        pred_y = prediction.data.numpy().squeeze()
        target_y = y.data.numpy()
        accuracy = sum(pred_y == target_y) / 150
        print('Accuracy=%.2f' % accuracy)
        ac_list.append(accuracy)
    if accuracy >0.99: #某个值以上停止训练
        print(t)
        break

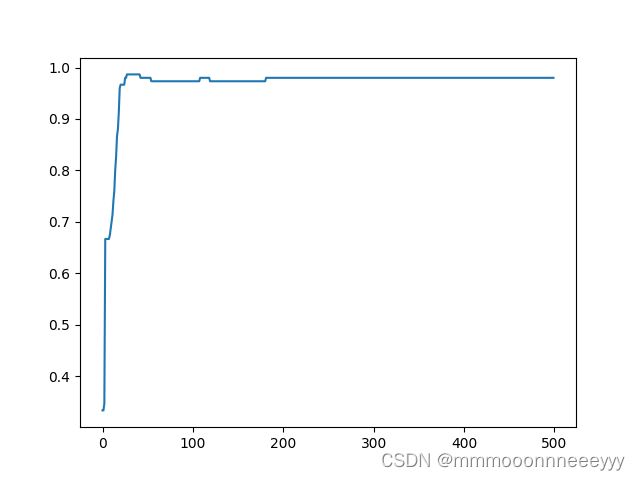
plt.plot(torch.arange(len(ac_list)),ac_list)
plt.show()


try_data=torch.tensor([5.8000, 3.0000, 5.1000, 1.8000]).to(dtype=torch.float32)
outt=net.forward(try_data)
_, pre = torch.max(F.softmax(outt),dim=0)
print(pre)
print(outt)

Accuracy=0.33
Accuracy=0.33
Accuracy=0.34
Accuracy=0.35
Accuracy=0.33
Accuracy=0.47
Accuracy=0.56
Accuracy=0.61
Accuracy=0.65
Accuracy=0.66
Accuracy=0.66
Accuracy=0.67
Accuracy=0.67
...
Accuracy=0.98
Accuracy=0.98
tensor(2)
tensor([-5.0852,  0.6899,  4.0998], grad_fn=)

4.5.1 小批量梯度下降法

为了减少每次迭代的计算复杂度，我们可以在每次迭代时只采集一小部分样本，计算在这组样本上损失函数的梯度并更新参数，这种优化方式称为小批量梯度下降法（Mini-Batch Gradient Descent，Mini-Batch GD）。
为了小批量梯度下降法，我们需要对数据进行随机分组。
目前，机器学习中通常做法是构建一个数据迭代器，每个迭代过程中从全部数据集中获取一批指定数量的数据。
输入层神经元个数为4，输出层神经元个数为3，隐含层神经元个数为6。

就改下这个：

banch_size=10

Accuracy=0.33
Accuracy=0.33
Accuracy=0.33
Accuracy=0.33
Accuracy=0.33
Accuracy=0.33
Accuracy=0.33
Accuracy=0.33
Accuracy=0.33
Accuracy=0.33
...
Accuracy=0.97
Accuracy=0.97
Accuracy=0.97
Accuracy=0.97
Accuracy=0.97
Accuracy=0.97
Accuracy=0.97
Accuracy=0.97
Accuracy=0.97
tensor(2)
tensor([-9.4600, -0.4949,  1.3191], grad_fn=)

思考题

1. 对比Softmax分类和前馈神经网络分类。（必做）
2. softmax代码在实验3
   softmax分类结果：

score/loss:0.734/0.505

前馈神经网络分类：

accuracy/loss:0.9823/0.2345

总结
3. 总结本次实验；
在使用小mbgd的时候学习了Torch的dataloader的使用。

4. 全面总结前馈神经网络，梳理知识点，建议画思维导图。