NNDL 实验三 线性回归

使用pytorch实现

2.2 线性回归

2.2.1 数据集构建

构造一个小的回归数据集：

生成 150 个带噪音的样本，其中 100 个训练样本，50 个测试样本，并打印出训练数据的可视化分布。

2.2.2 模型构建

2.2.3 损失函数

回归任务中常用的评估指标是均方误差

均方误差（mean-square error, MSE）是反映估计量与被估计量之间差异程度的一种度量。

【注意：代码实现中没有除2】思考：没有除2合理么？谈谈自己的看法，写到实验报告。

2.2.4 模型优化

经验风险 （ Empirical Risk ），即在训练集上的平均损失。

思考1. 为什么省略了不影响效果？

思考 2.  什么是最小二乘法 （ Least Square Method ， LSM ）

回答以上问题，写到实验报告。 

2.2.5 模型训练

在准备了数据、模型、损失函数和参数学习的实现之后，开始模型的训练。

在回归任务中，模型的评价指标和损失函数一致，都为均方误差。

通过上文实现的线性回归类来拟合训练数据，并输出模型在训练集上的损失。

2.2.6 模型评估

用训练好的模型预测一下测试集的标签，并计算在测试集上的损失。

2.2.7 样本数量 & 正则化系数

（1） 调整训练数据的样本数量，由 100 调整到 5000，观察对模型性能的影响。

（2） 调整正则化系数，观察对模型性能的影响。

---

2.3 多项式回归

2.3.1 数据集构建

构建训练和测试数据，其中：

训练数样本 15 个，测试样本 10 个，高斯噪声标准差为 0.1，自变量范围为 (0,1)。

2.3.2 模型构建

套用求解线性回归参数的方法来求解多项式回归参数

2.3.3 模型训练

对于多项式回归，我们可以同样使用前面线性回归中定义的LinearRegression算子、训练函数train、均方误差函数mean_squared_error。

2.3.4 模型评估

通过均方误差来衡量训练误差、测试误差以及在没有噪音的加入下sin函数值与多项式回归值之间的误差，更加真实地反映拟合结果。多项式分布阶数从0到8进行遍历。

对于模型过拟合的情况，可以引入正则化方法，通过向误差函数中添加一个惩罚项来避免系数倾向于较大的取值。

---

2.4 Runner类介绍

机器学习方法流程包括数据集构建、模型构建、损失函数定义、优化器、模型训练、模型评价、模型预测等环节。

为了更方便地将上述环节规范化，我们将机器学习模型的基本要素封装成一个Runner类。

除上述提到的要素外，再加上模型保存、模型加载等功能。

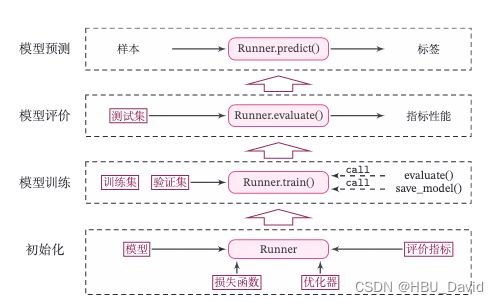
Runner类的成员函数定义如下：

• __init__函数：实例化Runner类，需要传入模型、损失函数、优化器和评价指标等；
• train函数：模型训练，指定模型训练需要的训练集和验证集；
• evaluate函数：通过对训练好的模型进行评价，在验证集或测试集上查看模型训练效果；
• predict函数：选取一条数据对训练好的模型进行预测；
• save_model函数：模型在训练过程和训练结束后需要进行保存；
• load_model函数：调用加载之前保存的模型。

---

2.5 基于线性回归的波士顿房价预测

使用线性回归来对马萨诸塞州波士顿郊区的房屋进行预测。

实验流程主要包含如下5个步骤：

• 数据处理：包括数据清洗（缺失值和异常值处理）、数据集划分，以便数据可以被模型正常读取，并具有良好的泛化性;
• 模型构建：定义线性回归模型类；
• 训练配置：训练相关的一些配置，如：优化算法、评价指标等；
• 组装训练框架Runner：Runner用于管理模型训练和测试过程；
• 模型训练和测试：利用Runner进行模型训练和测试。

2.5.1 数据处理

    2.5.1.2 数据清洗

    2.5.1.3 数据集划分

    2.5.1.4 特征工程

2.5.2 模型构建

2.5.3 完善Runner类

2.5.4 模型训练

2.5.5 模型测试

2.5.6 模型预测

---

【注意】例程2.5中有：

from nndl.op import Linear

from nndl.opitimizer import optimizer_lsm

这两个python文件位置如下：

文件使用了paddle，改写成pytorch，并在后续工作中使用即可。 

---

问题1：使用类实现机器学习模型的基本要素有什么优点？

问题2：算子op、优化器opitimizer放在单独的文件中，主程序在使用时调用该文件。这样做有什么优点？

问题3：线性回归通常使用平方损失函数，能否使用交叉熵损失函数？为什么？

---

ref：

NNDL 实验二（上） - HBU_DAVID - 博客园 (cnblogs.com)

NNDL 实验二（下） - HBU_DAVID - 博客园 (cnblogs.com)

---

3. 线性神经网络 — 动手学深度学习 2.0.0-beta1 documentation (d2l.ai)

• 3.1. 线性回归
  • 3.1.1. 线性回归的基本元素
  • 3.1.2. 矢量化加速
  • 3.1.3. 正态分布与平方损失
  • 3.1.4. 从线性回归到深度网络
  • 3.1.5. 小结
  • 3.1.6. 练习
• 3.2. 线性回归的从零开始实现
  • 3.2.1. 生成数据集
  • 3.2.2. 读取数据集
  • 3.2.3. 初始化模型参数
  • 3.2.4. 定义模型
  • 3.2.5. 定义损失函数
  • 3.2.6. 定义优化算法
  • 3.2.7. 训练
  • 3.2.8. 小结
  • 3.2.9. 练习
• 3.3. 线性回归的简洁实现
  • 3.3.1. 生成数据集
  • 3.3.2. 读取数据集
  • 3.3.3. 定义模型
  • 3.3.4. 初始化模型参数
  • 3.3.5. 定义损失函数
  • 3.3.6. 定义优化算法
  • 3.3.7. 训练
  • 3.3.8. 小结
  • 3.3.9. 练习