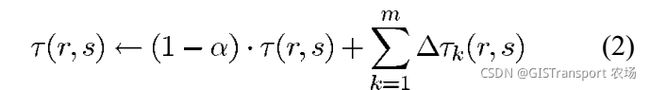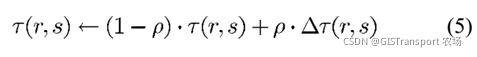蚁群算法求解旅行商问题详解

        在查找蚁群算法的资料时网上有很多讲解，细心的同学可能会发现，有几个热门的版本所介绍的蚁群算法有一些细微的差别，这是因为蚁群算法有很多种不同的变体，因此看到的介绍并不一致。所以决定从新将Marco Dorigo于1997年发表的文章Ant Colony System: A Cooperative Learning Approach to the Traveling Salesman Problem仔细的捋了一遍，并将其中的一些细节问题做了一些注解。

一、背景  

（一）旅行商问题（TSP）

      假设一个商人需要安排一次旅行，去拜访m个城市。商人选择从一个城市出发，要求途中经过所有城市且每个城市只能去一次，并且最后回到原点。旅行商的问题目标是求解一条长度（或开销）最短的路线。这是数学是的一个经典问题，这里不再累述。

（二）蚁群算法

        有群小蚂蚁住在蚂蚁镇A，有一只蚂蚁们听说B镇有一个大户人家里有二十万担粮食。蚂蚁们看了看家里的粮仓，家里食物已经不够过冬了，既然地主家还有这么多余粮，这样的好机会不允许错过。蚁王下令，让众蚂蚁出动去B镇把粮食运回来。在出动之前蚂蚁们拿出地图看了看，从A镇到B镇的道路四通八达，到底应该选择那一条路呢。于是乎，蚂蚁们一商量，想出了一个办法，不如先派一个小分队从不同的路线出发，去一趟B镇，到达之后大家合计一下看看哪一条路线更短，再决定应该选定哪一条路线去B镇。为了将行走的路线记下来，蚂蚁们约定在每次回来的时候在路线上要留下一个叫信息素的东西作为标记。   好了，第一批派出了一部分蚂蚁，目前所有的路上都还没有信息素，所以在每一个路口小蚂蚁选用的策略是选择面前最短的那一条路，按照这样的策略，小蚂蚁们陆续到达了终点。根据到达先后顺序，蚂蚁们判断出谁的路线更长、谁的路线更短，于是大家商量，按照路线从短到长的顺序，大家原路返回，且路线短的蚂蚁在回城的路上留下更多的信息素，路线长的蚂蚁则在途径的路上留下更少的信息素。

        当第一批蚂蚁们都顺利回到老窝之后。现在蚂蚁们可以正式出发了，小蚂蚁们每到第一个路口，首先看看备选路线中每条路线的长短和路线上的信息素，然后优先选择长度短、信息素更高的路线。以此为依据，蚂蚁到每一个路口的时候都按照这个规则进行判断，最终到达终点，按照这样的规则蚂蚁们有很大概率会找到一条比较短的路线。当然，在正式出发前，也可以多派几批蚂蚁出发，然后沿按照相同的程序根据路线的长短在回程的路上留下信息素。由于多批蚂蚁出门所以有更多探索新路线的可能，这样有助于在正式出发时找到最短路径。

       上面这个故事讲完，可能大家对蚁群算法求解TSP 问题有了一个基本的了解，是不是还挺简单，是不是也还有一些困惑？下面开始讲解基于蚁群算法的TSP问题解决方案，首先是对基础版本的求解算法进行介绍，然后再描述升级版本求解方案。

二、基础版的蚁群算法求解TSP问题

        假设有m个城市，每次派出n只蚂蚁，每只蚂蚁随机选择一个出发城市（即选择N个城市）。现在我们把目光对准一只蚂蚁小k，小k来到了一个城市 r，摆在它面前的是很多个城市，到底应该选哪一个呢，那么我们先采用一个启发式的方式。我们通过一个概率的方式来对不同选择进行建模，假设下s 是下一个备选城市中的一个, 那么我们从以下两个方面考虑选择城市s 的概率：

       1）r 到 s 这条路上信息素是多少，根据蚁群觅食过程中寻路的过程，我们知道一条路信息素越高越好

       2）r 到s 的距离是多少，这里采用一个启发式的策略，认为r 到s 的距离越短越好

       那么综合考虑这两点，就可以构建一个公式来描述从r 到s 的转移概率分布

其中的表示是小蚂蚁k从城市r选择城市s的概率，表示的是从r到s路线上的信息素，  表示的是r到s的距离，β 表示权重，用于平衡信息素和距离两个因素影响的权重。表示所有和城市r 相连接的城市集合。具体实现上是采用随机概率规则（random-proportional rule）来选择下一个城市。

        我们说过蚂蚁通过探索的方式来实现对每条路上的信息素的更新，那么该如何更新，我们假设n只蚂蚁已经完成了城市旅行任务，即从初始城市出发，经过了中间的所有城市，然后回到了原点。对于路段更新的公式如下：

 

其中的0<α<1 , 则可知0<（1-α）<1 。回忆一下，我们说过蚂蚁的信息素是会随着时间蒸发的，这里(1-α )表示是蒸发之后的信息素，α 自然表示的也就是蒸发率。  则表示所有n只蚂蚁通过路段引入的信息素增量。信息增量的总体原则是总路程更短的蚂蚁所通过路段的信息增量应该比那些总路程长的蚂蚁所通过的路段的信息增量多（这个有点类似强化学习框架，即好的方案会得到更多的强化）。其中表示的是蚂蚁k的行程距离，因此在取到数以后也就满足路线越短增益越高。这里可以知道信息素就像是一个长期记忆存储箱，存储在每条边上，而不是存储在单个的蚂蚁身上。

        以上就是基础版本蚁群算法了，在正式算法运行过程中，我们需要进行多次迭代（每一次迭代指的是：所有蚂蚁重新从第一次的初始位置出发完成所有城市旅行并回到原点）。另外在第一次迭代中还涉及到每条边信息素的初始化、α 值、以及初始化蚂蚁数量n的值。

三、升级版蚁群算法

      传统的蚁群算法对于小的TSP问题的寻优效果可能较好，但是对于大的TSP（城市数量大）问题，求解的速度很慢。同时也还存在以下问题：

1. 随着道路的信息素增高，传统的方法可能会影响蚂蚁探索新的道路，导致多次迭代后的最优解没有提升
2. 运行的速度较慢，可以考虑对信息素的更新方式做一个改进

针对以上两个问题，可以从下面三个方面传统的蚁群算法进行改进：

1. 转移概率计算，计算从r具体选定哪一个s, 按照如下公式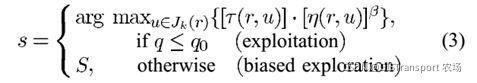

其中 q 是一个从[0,1]均匀分布中抽取的一个平均数，  则是设定的一个参数。可到了解，当随机数的值小于时，我们采取一种选择最优的边, 反之（即s=S时）我们还是采用与传统方式一致的随机概率规则来选取下一条边（公式（1））。从中可知，q<的设定中，如果是exploitation（开采模式）表示我们直接选用最优的边，反之，如果是biased exploration（带概率分布的探索）表示我们根据概率分布来选择下一个城市。

2. 全局更新规则

       我们之前讲过信息素的更新规则主要是为了给那些路程短的蚂蚁所通行的路段添加增加更多的信息素。那么既然是这样的话，我们可以考虑只根据迭代中的最优结果所包含的路段进行信息素更新，其他非最优旅行通过的路段的信息素不做更新，这样可以大大的较少信息素更新的次数。新的更新规则到如下

其中表示的是到目前为止，迭代中产生的最优解。另一种更新的方式才是使用来代替，其中表示一次迭代中的最优解。原文的研究表明和两种更新方式产生的结果类似，的结果稍微更好点。

3. 局部更新规则

 

 其中0<ρ<1 , 这种局部更新规则是受到采用Q-learning来解决强化学习问题的启发。核心的思路是当采取一个行动以后，立即对进入该行动进行评价。对应更新方式为

  

其中表示的是选择了s 以后，所有与s相连的城市路段总信息素最大的城市。另一种方法则是直接设定,其中  表示的是初始信息素大小。原文通过实验说明两种更新方式的效果差不多，很明显，由于的更新方法更简单，所以推荐采用这种方法。局部更新的目的为了保证两个城市之间的边在每次访问过之后信息素做少量的减少（因为  总是最小，即满足），这样可以部分综合由于全局更新造成信息素增长。如果没有局部更新规则，那么所有蚂蚁在搜索下一个的城市的时候将很有可能局限在上一个最优路线的周围。

四、程序实现

       1)  ACS解决TSP问题的简单实现（C++）

       2)  蚁群算法（Ant Clony Optimization）

五、参数设置

        β 值: 2

          值（状态转移方法阈值）：0.9 

        : 一般设定为 , n 为城市数量为根据最邻近（nearest neighbor）启发式算法得到路线长度。

        α 值（全局更新的蒸发率）：0.1

        ρ 值（局部更新的蒸发率）：0.1

        初始化蚂蚁数量n的值：设定为10，文中提供了一种设置的方法。如果不知道怎么设置的话，一般情况下的可以设置n=m。

六、后记

       原文中还详细的论述了如何对初始化蚂蚁数量n进行设定，以及对加入局部更新之后的效果评估等问题，有兴趣需要深入了解的同学建议查看原文。其实仔细想想，蚁群算法可以作为很多启发式寻路算法的改进版本，核心是设定合理的信息素更新方式，当然蚁群算法涉及多次迭代和多只蚂蚁，计算的成本自然也会上升。