图像拼接论文-视差问题的解决、射影和 仿射变换、

Constructing Image Panoramas using Dual-Homography Warping                Michael S. Brown

This paper describes a method to construct seamless im-age mosaics of a panoramic scene containing two predom-inate planes: a distant back plane and a ground plane that sweeps out from the camera's location.

相机可以不遵循images are of a distant scene or images arecaptured by rotating the camera about its center of projec-tion这两个条件（传统的自动拼接必须遵循这两个条件）

但是Our approach fails when the scene contains a relatively large structure that does not belong to either the groundplane nor distant plane. In such case, the parallax effect will occur since there are more than two homographies in-volved. 

 

今后研究发展前景：A natural extension of our work is to consider more than two planes. This extension can quickly drive itself towardsfull 3D scene understanding and ultimately proxy geometry estimation in a shape from motion setting. Determining the minimum number of planes to estimate to maintain a seam-less panorama in a given scene is an interesting avenue forfuture work.

Smoothly Varying Affine Stitching    Wen-Yan Lin1Siying Liu1

研究了将

阐明了为什么不用3D拼接

Unfortunately, dense feature descrip-tors such as those used in SIFT flow [15], introduce a lot oflocalization error as neighboring pixels are likely to share similar feature descriptors, thus making accurate dense de-scriptor based matching difficult.

As-Projective-As-Possible Image Stitching with Moving DLT

We investigate projective estimation under model inadequacies, i.e., when the underpinning assumptions of the projective model are not fully satisfied by the data. We focus on the task of image stitching which is customarily solved by estimating a projective warp - a model that is justified when the scene is planar or when the views differ purely by rotation. Such conditions are easily violated in practice, and this yields stitching results with ghosting artefacts that necessitate the usage of deghosting algorithms. To this end we propose as-projective-as-possible (APAP) warps, i.e., warps that aim to be globally projective, yet allow local non-projective deviations to account for violations to the assumed imaging conditions.

Figure 2: 1D analogy of APAP warp to fit a set of 1D correspondences (x,x'). (a) A normal projective warp cannot capture the local variations due to violations to the imaging assumptions (pure rotational camera motion). (b) An APAP warp is globally projective to respect the effects of a pin-hole projection, but can vary locally to account for deviations to the imaging assumptions.

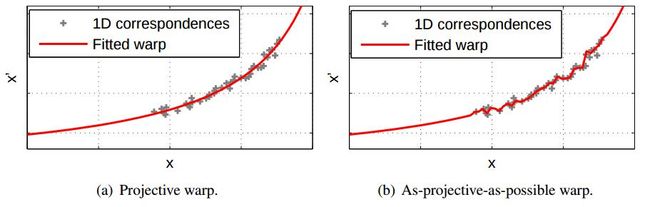
Based on a novel estimation technique called Moving Direct Linear Transformation (Moving DLT), our method seamlessly bridges image regions that are inconsistent with the projective model; see Figure 1. The result is highly accurate image stitching, with significantly reduced ghosting effects, thus lowering the dependency on post hoc deghosting.

• [MDLT code]
  Stitches two overlapping images using an APAP warp estimated using Moving DLT (essentially this is the code for the CVPR 2013 paper).
  
  
• [BAMDLT code]
  Stitches multiple overlapping images using multiple APAP warps estimated using Bundled Moving DLT (essentially this is the code for the TPAMI 2014 paper).
  Compatibility: The code was tested with MATLAB 2013 and 2014. MATLAB 2015 changed its pooling functions, so you may have to change the code if you receive an error message when running in MATLAB 2015.
  Dependencies: You will need to install EIGEN and Google's Ceres solver and link them to your MATLAB command line when you build the corresponding MEX files

Processing pipeline of our MDLT code (pairwise stitching without bundle adjustment):

1. Read pair of images to stitch (image I and image I').
2. Obtain SIFT keypoint matches between I and I'.
3. Remove incorrect keypoint matches (outliers) by means on RANSAC.
4. Obtain matrix A from the set of N correct keypoint matches ({x_i,x_i'} for i=1,…,N) after RANSAC.
5. Generate mesh (of size C1 x C2) over image I.
6. (perform Moving DLT) For each vertex x* on the mesh:
   1. Obtain matrix W* which contains the weights between x* and all x_i for i=1,…,N.
   2. Perform SVD on matrix repmat(W*,1,9).*A.
   3. Obtain homography H* from the least significant right singular vector of W*A.
7. Composite the images:
   1. Obtain offset between I' and warped I.
   2. Make "blank" canvas (the canvas will contain image I' and the warped image I).
   3. Copy I' to the canvas in the position determined by the offset.
   4. For each pixel coordinate p in image I, obtain the nearest mesh vertex x*.
      1. Use the homography H* from the nearest x* to warp p in I to p' in I'.
      2. Obtain the average of the intensity of pixels I(p) and I'(p').
      3. Put averaged pixel in canvas (in coordinate p' + offset).

On step 6(b) of the pseudo-code, the size of matrix A is 2N x 9 and the size of W* is 2N x 1, the ".*" operator means element-wise multiplication and repmat is MATLAB's replicate and tile array function.

we categorise previous works into two groups: (1) methods that reduce ghosting by construct-ing better alignment functions, and (2) methods that reduceghosting after alignment using advanced methods in com-positing, pixel selection or blending. In the second group,seam cutting [1, 3] and Poisson blending [13] are influential. Since our approach belongs to the first group, we re-view such methods in the following. Ideally, methods from both groups should be jointly used for best results.

We first review the estimation of projective transformations customarily used in image stitching, and then describethe proposed as-projective-as-possible warp.

融合算法seam cutting and straightening such as in [4]J. Gao, S. J. Kim, and M. S. Brown. Constructing im-age panoramas using dual-homography warping. In CVPR,2011. 

advanced blending or pixel selection [17]R. Szeliski. Image alignment and stitching. In Handbook ofMathematical Models in Computer Vision, pages 273–292.Springer, 2005.

 pyramid blending [17] is sufficient toaccount for exposure differences and to smoothen the blend.

 multi-band blending algorithm