matlab 电路频率响应_频率响应法与matlab指令计算
提要:前面考察了阶跃信号和斜坡信号的测试输入信号的应用。现在研究系统对正弦输入信号的稳定性。线性定常系统对正弦输入信号的响应,是具有相同频率、不同幅值和相角的正弦信号。引入伯德图的方法,讨论频率特性的极坐标图和对数幅相图,重新考虑系统的几种时域指标,并引入系统带宽的概念。
引言:前面的章节,利用复变量s及s平面上的零点和极点分布来刻画系统的响应和性能。这里是介绍另一种非常重要而且实用的系统分析和设计方法—频率响应法。
收获
(1)频率响应的基本概念及其在控制系统设计中的应用;
(2)手绘伯德图的方法和用matlab计算伯德图;
(3)三种坐标表述:极坐标图、伯德图、对数幅相图;
(4)用频率响应法设计控制器,并满足预期的指标要求。
一. 基本概念
- 频率响应
系统的频率响应定义是,系统对争先输入信号的稳态响应。正弦信号是一种独特的输入信号,在它的激励下,系统的输出信号及内部个节点的信号,在系统达到稳态时均为正弦信号,而与输入信号相比,它们的频率相同,只有幅值和相角不同。
2. 频率响应的优点
(1)由于可以方便地得到各种频率和幅值的正弦输入信号,因此我们能够用试验的手段精确地得到系统的频率响应,这是一种既可靠又不复杂的控制系统试验分析方法;
(2)当系统传递函数未知时,可以用试验的方法,通过测量频率响应来推导系统的传递函数;
(3)在频率域内进行系统设计时,还能够有效地控制系统带宽,从而达到控制噪声和干扰的目的;
(4)方便得到,只要用jw替换复变量s,就能够由传递函数T(s) 直接得到系统的频率特性函数T(jw),它包含了幅值和相角两个因素,通常用图形或曲线来表示T(jw) 的幅值和相角随频率变化的情况,它们能深刻地揭示控制系统分析和设计的内涵。
3. 频率响应法的不足
不足之处在于频率域和时间域之间没有直接的联系,在实际设计工作中,还是有一些近似设计准则。
4. 极坐标图
将系统的传递函数G(s) 改写为频率特性函数,即
5. 对数坐标图/伯德图
假设系统在频率域内的传递函数为
6. 转折频率/转角频率
假设频率特性传递函数为
7. 十倍频程
在相频特性曲线中,将两个频率点之间相差10 倍记为十倍频程,类似地有二倍频程的概念
8. 非最小相位传递函数
之前的接触中,G(s) 的零点和极点都处在 s 左半平面,但实际上,一个系统也可能有位于 s 右半平面的零点,此时系统仍然可能是稳定的。在 s 右半平面有零点的传递函数称为非最小相位传递函数。
9. 最小相位传递函数
把零点全部位于 s 左半平面的传递函数
10. 最小相位
最小相位系统
11. 全通网络
一个有趣的非最小相位系统,它具有对称的网络结构。
12. 谐振峰值
谐振峰值
13. 系统带宽
系统带宽
14. 对数幅相图
在一定的频率变化范围内,直接绘制对数幅值增益随相角的变化曲线,所得到的图形就称为对数幅相图。(得到对数幅相曲线较为简便的方法是,先绘制伯德图,再将其中的信息转换到由对数幅值和相角构成的坐标系中),在研究频率域内的稳定性时,就会用到对数幅相图,并用它来研究闭环反馈控制系统的相对稳定性。
二. 基本知识回顾
- 拉普拉斯变换对的定义
2. 类似地,也给出了傅里叶变换对的定义
3. 拉普拉斯变换与傅里叶变换
如果已知
各有所长,各有侧重。由拉普拉斯变换可以导出系统的传递函数T(s),基于拉普拉斯变换的 s 平面方法侧重于分析系统的零点和极点分布。而由傅里叶变换可以导出系统的频率特性函数T(jw) ,基于傅里叶变换的频率响应法将重点转向了系统的幅频特性和相频特性。
4. 频率特性函数中的时钟基本因子项
(1)常数增益:
常数项
其相角为
因此,在伯德图上,其对数增益曲线是一条水平线。而当增益是负值时,其对数增益仍然是
(2)原点处的极点或零点项:
考虑原点处的极点项,它对应的对数幅值增益为
对应的相角为
多重极点,则曲线斜率变为
考虑原点处的零点,它对应的对数幅值增益为
对应的相角为
(3)实轴上的极点或零点项:
考虑实轴上的极点项
其对数幅值增益为
实极点项的相角的表示为
考虑实零点项
渐近线的斜率变为
(4)共轭复极点或零点项:
共轭复极点对应的二阶基本因子项的典型形式为
共轭复极点项的对数幅值增益为
相角为
分析:当u<<1时,对数幅值增益为
当u>>1时,对数幅值增益近似为
注意这两条渐近线在频率点
谐振频率
与此频率对应的幅值最大值为
5. 伯德图的绘制
将每个零点和Ian 极点因子项的伯德图叠加起来,就可以的带含有多个零点和极点的传递函数
6. 频率响应测量
正弦信号可以用来测量控制系统的开环频率响应,实际的测量结果通常是幅值和相角随频率的变化曲线。利用这两条曲线,就可以导出系统的开环频率特性函数
7. 频域性能指标
如何将系统的频域响应和时域响应结合起来?(超调量、调节时间、平方误差等)
考虑一个前向通道函数为
对二阶系统而言,谐振峰值
谐振频率
谐振峰值
频率响应的系统带宽与固有频率之间近似存在着线性回归的关系。
三. 使用matlab计算
使用的函数是 bode(绘制伯德图,bode(sys)既适用于传递函数的形式,也适用于状态空间的形式) 和 logspace(用于生成对数刻度的频率点向量)
在学习过程中,培养手工绘制伯德图的能力才是最基础、最重要的工作,勤于动手才能深入理解和掌握控制系统的理论和方法。
1 绘制伯德图
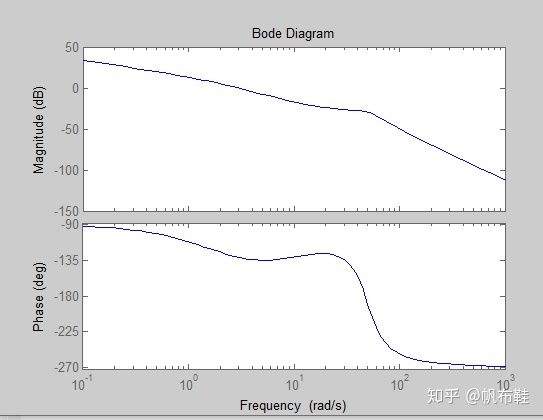
绘制伯德图,考虑传递函数
% The Bode plot of
%
% 0.5 s + 5
% G(s) = ----------------------------------------
% 0.0002 s^4 + 0.0064 s^3 + 0.512 s^2 + s
%
% using the logspace function to generate
% the frequency points.
%
num=5*[0.1 1];
den=[0.0002 0.0064 0.5120 1 0];
sys=tf(num,den);
w=logspace(-1,3,200);
bode(sys,w);上图中,函数bode自动选择了频率变化的范围,也可以使用函数logspace来指定生成这个范围。
2. 时域和频域之间的关系
控制系统的设计目的是使系统满足给定的时域性能指标的要求,因此在频域内设计控制系统时,应当首先建立频率响应和时域响应的相互联系。而且,这两个问题域中的指标之间的联系完全取决于系统能否用主导极点近似二阶系统,以及近似的精确程度。幸运的是,大部分实际控制系统都有二阶主导极点,因而能够用二阶系统降阶近似。
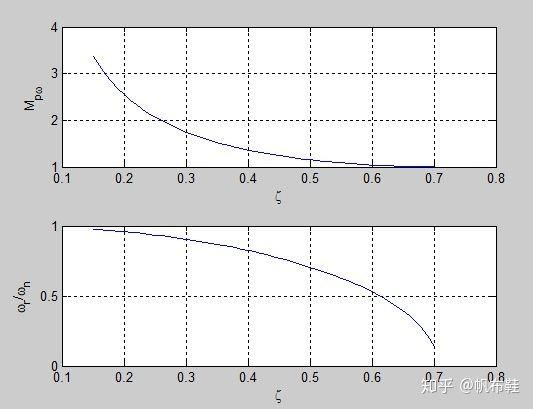
考虑典型的二阶系统,其闭环传递函数为
% The relationship between (Mpw,wr) and (zeta,wn) for
% a second-order system.
%
zeta=[0.15:0.01:0.7];
wr_over_wn=sqrt(1-2*zeta.^2);
Mp=(2*zeta .* sqrt(1-zeta.^2)).^(-1);
%
subplot(211),plot(zeta,Mp),grid
xlabel('zeta'), ylabel('M_{pomega}')
subplot(212),plot(zeta,wr_over_wn),grid
xlabel('zeta'), ylabel('omega_r/omega_n')则可以得到二阶系统的谐振频率
3. 使用频率响应法来设计控制系统的步骤
假设闭环传递函数是
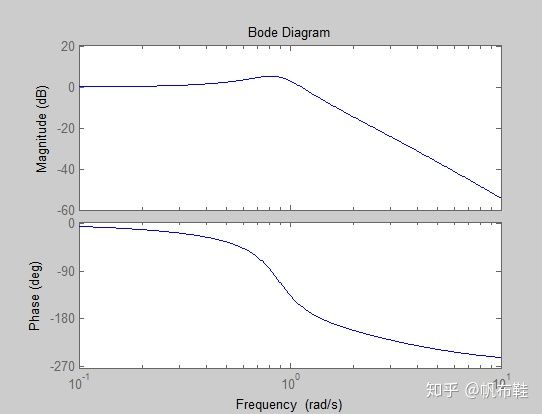
(1)给定一个初始值K(例如程序中给定K=2),绘制闭环伯德图
% Closed-loop peak magnitude and resonant frequency for
%
% K
% T(s) = -------------- ,
% s^3+3s^2+2s+K
%
% where K must be input at the command level prior to
% executing this m-file.
%
% Rename this script engrave1.m for use with book
%
K=2;
num=[K]; den=[1 3 2 K]; sys=tf(num,den);
w=logspace(-1,1,400);
bode(sys,w);
[mag,phase,w]=bode(sys,w);
[mp,l]=max(mag);wr=w(l);
mp,wr
zeta = sqrt(0.5*(1-sqrt(1-1/mp^2)));
wn = wr/sqrt(1-2*zeta^2);
ts=4/zeta/wn
po=100*exp(-zeta*pi/sqrt(1-zeta^2)) 2. 通过上图中的伯德图,确定谐振峰值
在上述m脚本文件中可以得到
3. 通过频域性能指标和时域性能指标之间的关系
来求取固有频率
4. 验证时域性能指标
调节时间
超调量
% The step response of the engraving machine, where
%
% 2
% T(s) = ------------- .
% s^3+3s^2+2s+2
%
K=2; num=[K]; den=[1 3 2 K];
sys=tf(num,den);
t=[0:0.01:20];
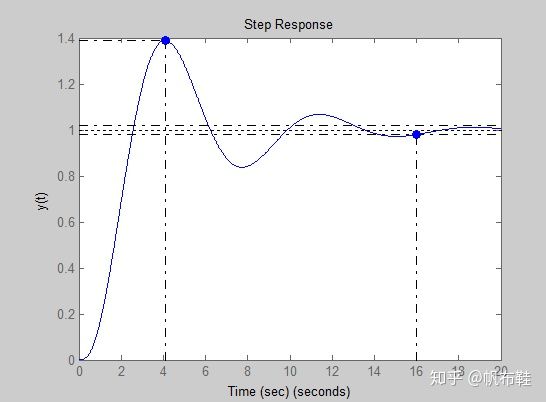
step(sys,t);
xlabel('Time (sec)'), ylabel('y(t)')从图中可以看出,超调量为39%,调节时间为16s
与前面进行估算的值基本一致。
5. 更新参数K
知道达到理想中的时域性能指标。