【机器学习】评价指标 : 准确率,查准率与查全率
引言
在机器学习中,有几个评价指标,今天专门来介绍一下。之前的学习中主要是看模型,学算法,突然有一天发现,机器学习中的一些基本概念还是有点模糊,导致不知道如何综合评价模型的好坏。 这篇文章主要介绍如下几个知识点:
Accuracy(准确率)
Precision(精确率,差准率)
Recall(召回率, 查全率)
ROC曲线
AUC面积
介绍
- 正样本 : 属于某一个类别(真值)的样本
- 负样本 : 不属于某一个类别的样本
个人理解,正负样本是相对的,取决于机器学习算法开发者。
TP(True Positive) : 猜对了; 预测为正样本
TN(True Negative): 猜对了; 预测为负样本
FP(False Positive): 猜错了: 预测为正样本
FN(False Negative): 猜错了: 预测为负样本
Accuracy(准确率)
我们想计算一下模型的准确率, 不就是拿 (我们模型猜对的数据个数) / (所有的的数据个数)
即 :(TP + TN) / (ALL)
当然了, 我们希望, 模型的准确率越高越好,最好是猜的全对~
Precision(精确率, 查准率)
在某些场景下,我们希望模型是这样, 如果模型猜测某个样本为正样本, 它尽可能的就是正样本。
也就是说,这个评价指标里,我们不考虑模型把正样本猜成负样本的场景,但是只要模型说这个是正样本,大概率就是正样本。
计算公式: TP / (TP + FP)
举个例子: 宁可漏掉,也不能错杀。 在垃圾邮件的识别过程中,希望宁可漏掉,也不要把正常的邮件给拦截了。
考虑极端场景:
- 如果百万数据中,我模型就判断了一个正样本,并且猜对了, 这个指标就是 100% 了。
- 如果百万数据中,我模型全部判断为负样本, 这个指标就是 0/0 就没有值了。
Recall(召回率, 查全率)
然而,在某些场景下, 我们又希望模型是这样的,模型可以把尽可能多的正样本都猜出来。
计算公式: TP / (TP + FN)
举个例子: 宁可错杀,也不能漏掉, 如果漏掉一个正样本的判断,会产生灾难性影响的场景下, 这个指标就非常重要了。
考虑极端场景:
- 我模型全部判断样本为正样本, 这样的指标就是100%
- 我模型全部判断样本为负样本, 这样的指标就是0%
简单的思考下可以知道,如果我们只追求单个查准率 或 查全率,这是不合理的,没有实际的价值,因此,需要综合考虑多个因素。
参考文档:
https://zhuanlan.zhihu.com/p/152197756
PR曲线
PR曲线: recall 为横坐标, precision为纵坐标。
思考一下可以知道, PR曲线越往右上凸起,效果越好。
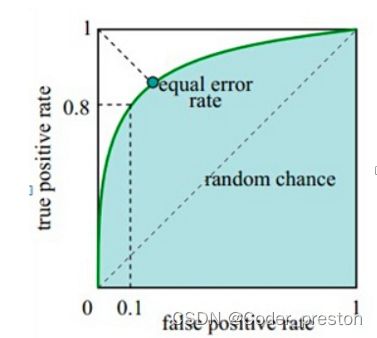
ROC曲线
要理解ROC曲线, 需要理解两个概念, 分别代表着X轴与Y轴
x 轴:FPR(False Postive Rate)
FPR = FP / (FP + TN) (猜错的正例) / (观测值里所有的反例)
y 轴:TPR (True Postive Rate)
TPR = TP / (TP + FN) (猜对的正例) / (观测值里所有正例)
- 横轴FPR:,FPR越大,预测正类中实际负类越多。
- 纵轴TPR:TPR越大,预测正类中实际正类越多。
理想目标:TPR=1,FPR=0,即图中(0,1)点,故ROC曲线越靠拢(0,1)点,越偏离45度对角线越好,Sensitivity、Specificity越大效果越好.
说一下个人对这个曲线的理解, 是干货哦,是自己一开始对这个曲线最大的疑惑,后来想通了
图中的曲线,似乎无线趋近于(1,1)这个点, 这个点表示什么意思呢?思考了一下,得到如下的结论:
x 轴的 1 表示: 如果一个模型越是把负类预测为正类。(如果所有的负类都被猜成正类了)
y 轴的 1 表示: 那么这个模型就越容易把正类也预测为正类。(所有的正类也很可能会被猜成为正类。)
那么,这个曲线是什么样的才是一个好的模型呢?
我们希望
一个模型越不容易把负类预测为正类的情况下,(x越小)
这个模型越容易把正类预测为正类 (y越大)
所以说,曲线越是往左凸出,模型越好。
这样解释的话,是不是就理解曲线的含义了呢?
那么问题来了,我们应该怎么得到ROC曲线一系列的坐标点的数据呢?有了坐标点,我们才可以画曲线。
答案如下:在模型的预测结果中,一般预测的结果是这个样本为正样本的概率,概率越大, 则越可能是正样本;因此可以设置一个阈值,大于这个阈值的,就是正样本。
但是, 阈值选取多大比较合适呢? 我们可以选取各种不同的阈值,求出该阈值条件下的FPR和TPR的值,获得的坐标点就是ROC曲线中的点了。
ROC曲线与PR曲线的对比
主要参考:https://zhuanlan.zhihu.com/p/138181502
- ROC曲线:当测试集中的正负样本的分布变化的时候,ROC曲线能够保持不变
- PR曲线 : 对于只关心正例的场景,则由于PR曲线使用了Precision,因此PR曲线的两个指标都聚焦于正例。所以在此情况下PR曲线被广泛认为优于ROC曲线。
使用场景:
- ROC曲线由于兼顾正例与负例,所以适用于评估分类器的整体性能,相比而言PR曲线完全聚焦于正例。
- 衡量模型时,如果想剔除类别分布带来的影响, 则ROC比较合适。
- 如果在相同类别分布下, 想看正例的预测情况, 则PR比较合适。
- 类别不平衡问题中, ROC曲线通常会给出一个乐观的效果估计,考虑使用PR曲线。
- 在曲线上找到一个最优的点, 从而得到阈值 和 precision, recall等重要指标,并应用于实际场景。
AUC面积
定义: AUC面积指的是 ROC曲线下的面积。
我们如何从AUC来判断模型的优劣标准呢?
参考:https://blog.csdn.net/u013514928/article/details/106635778
AUC = 1,是完美分类器,采用这个预测模型时,存在至少一个阈值能得出完美预测。绝大多数预测的场合,不存在完美分类器。
0.5 < AUC < 1,优于随机猜测。这个分类器(模型)妥善设定阈值的话,能有预测价值。
AUC = 0.5,跟随机猜测一样(例:丢铜板),模型没有预测价值。
AUC < 0.5,比随机猜测还差;但只要总是反预测而行,就优于随机猜测。
总结
这篇文章主要介绍了机器学习模型的评价指标以及相关评估曲线。 在机器学习中, 我们除了需要学习研究算法的原理, 也要知道如何来评估一个模型 ,以及如何选取阈值参数。 在选择评价指标的时候, 也需要根据具体的场景, 选择合适的评价指标,从而可以客观的评价模型孰优孰劣。