PCL 二次曲面拟合并计算曲率
一、数学上的二次曲线方程
【高等数学】九种标准二次曲面 - 知乎
在笔记本上推导二次曲面的计算曲率以及第一 第二基本不变量,感觉太花时间了,等后面有时间了在不进去。
二次曲面拟合求点云的曲率_点云侠的博客-CSDN博客_二次曲面拟合求点云的曲率
下面的所有数学推导都是摘抄自上面那篇博客,只是学习而已。
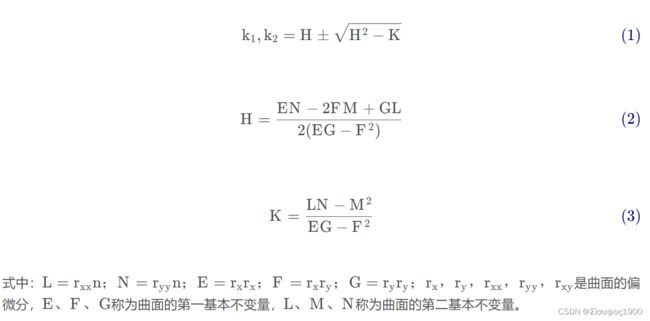
点云中任意的一个点的,可以是用临近半径或者临近点来找到一些局部点,用这些局部的点可以拟合一个局部的曲面,那么这个点的曲率就是由改点和周围临近点拟合的局部曲面的曲率,通过最小二乘法我们可以拟合这个二次曲面,同理我们可以计算出该点的主曲率k1 k2,那么平均曲率H和高斯曲率K之间的关系如下:
二、计算曲率
在点云中任取一点p1,然后使用ksearch 的方法搜索到周围的n个点,拟合一个局部二次曲面:
三、曲面类型
通过高斯曲率和平均曲率来判断曲面的几何类型
四、程序显示
#if 1 // 使用二次曲面来技术点云的高斯 平均曲率
using namespace Eigen; // 矩阵
int main()
{
pcl::PointCloud::Ptr cloud(new pcl::PointCloud);
if (-1 == pcl::io::loadPCDFile("Horse.pcd", *cloud))//放到与工程中的主.cpp同一位置的文件夹下
{
cout << "加载文件失败!" << endl;
return -1;
}
cout << cloud->points.size() << endl;
//---------------矩阵运算相关参数-------------------
MatrixXd Mean_curvature;
Mean_curvature.resize(cloud->size(), 1); //初始化矩阵 cloud->size * 1;
MatrixXd Gauss_curvature;
Gauss_curvature.resize(cloud->size(), 1);
MatrixQ; //求解方程组系数矩阵 6 * 6 的矩阵
MatrixQ_Inverse; //系数矩阵的逆矩阵
MatrixB; //方程组右值矩阵 线性方程组
Q.setZero(); //初始化矩阵元素全为0
Q_Inverse.setZero();
B.setZero();
//------------K近邻搜索查找最近点----------------
pcl::KdTreeFLANN kdtree;
kdtree.setInputCloud(cloud);
for (size_t i_p = 0; i_p < cloud->points.size(); ++i_p)
{
int K = 10; //设置需要查找的近邻点个数
vector pNK(K); // 保存每个近邻点的索引
vector pointNKNSquaredDistance(K); // 保存每个近邻点与查找点之间的欧式距离平方
if (kdtree.nearestKSearch(cloud->points[i_p], K, pNK, pointNKNSquaredDistance) > 0)
{
double a = 0, b = 0, c = 0, d = 0, e = 0, f = 0;//二次曲面方程系数
double u = 0, v = 0; //二次曲面参数方程参数
double E = 0, G = 0, F = 0, L = 0, M = 0, N = 0;//曲面第一、第二基本量
double Meancurvature = 0, Gausscurvature = 0; //平均曲率、高斯曲率
for (size_t i = 0; i < pNK.size(); ++i)
{
//---------------构建最小二乘平差计算矩阵-------------------
Q(0, 0) += pow(cloud->points[pNK[i]].x, 4);
Q(1, 0) = Q(0, 1) += pow(cloud->points[pNK[i]].x, 3) * cloud->points[pNK[i]].y;
Q(2, 0) = Q(0, 2) += pow(cloud->points[pNK[i]].x * cloud->points[pNK[i]].y, 2);
Q(3, 0) = Q(0, 3) += pow(cloud->points[pNK[i]].x, 3);
Q(4, 0) = Q(0, 4) += pow(cloud->points[pNK[i]].x, 2) * cloud->points[pNK[i]].y;
Q(5, 0) = Q(0, 5) += pow(cloud->points[pNK[i]].x, 2);
Q(1, 1) += pow(cloud->points[pNK[i]].x * cloud->points[pNK[i]].y, 2);
Q(2, 1) = Q(1, 2) += pow(cloud->points[pNK[i]].y, 3) * cloud->points[pNK[i]].x;
Q(3, 1) = Q(1, 3) += pow(cloud->points[pNK[i]].x, 2) * cloud->points[pNK[i]].y;
Q(4, 1) = Q(1, 4) += pow(cloud->points[pNK[i]].y, 2) * cloud->points[pNK[i]].x;
Q(5, 1) = Q(1, 5) += cloud->points[pNK[i]].x * cloud->points[pNK[i]].y;
Q(2, 2) += pow(cloud->points[pNK[i]].y, 4);
Q(3, 2) = Q(2, 3) += pow(cloud->points[pNK[i]].y, 2) * cloud->points[pNK[i]].x;
Q(4, 2) = Q(2, 4) += pow(cloud->points[pNK[i]].y, 3);
Q(5, 2) = Q(2, 5) += pow(cloud->points[pNK[i]].y, 2);
Q(3, 3) += pow(cloud->points[pNK[i]].x, 2);
Q(4, 3) = Q(3, 4) += cloud->points[pNK[i]].x * cloud->points[pNK[i]].y;
Q(5, 3) = Q(3, 5) += cloud->points[pNK[i]].x;
Q(4, 4) += pow(cloud->points[pNK[i]].y, 2);
Q(5, 4) = Q(4, 5) += cloud->points[pNK[i]].y;
Q(5, 5) += 1;
B(0, 0) += pow(cloud->points[pNK[i]].x, 2) * cloud->points[pNK[i]].z;
B(1, 0) += cloud->points[pNK[i]].x * cloud->points[pNK[i]].y * cloud->points[pNK[i]].z;
B(2, 0) += pow(cloud->points[pNK[i]].y, 2) * cloud->points[pNK[i]].z;
B(3, 0) += cloud->points[pNK[i]].x * cloud->points[pNK[i]].z;
B(4, 0) += cloud->points[pNK[i]].y * cloud->points[pNK[i]].z;
B(5, 0) += cloud->points[pNK[i]].z;
//---------------求解矩阵------------------
Q_Inverse = Q.inverse();
for (int j = 0; j < 6; ++j)
{
a += Q_Inverse(0, j) * B(j, 0);
b += Q_Inverse(1, j) * B(j, 0);
c += Q_Inverse(2, j) * B(j, 0);
d += Q_Inverse(3, j) * B(j, 0);
e += Q_Inverse(4, j) * B(j, 0);
f += Q_Inverse(5, j) * B(j, 0);
}
}
// 根据所求曲面方程的系数计算曲面第一第二基本量
u = 2 * a * cloud->points[i_p].x + b * cloud->points[i_p].y + d;
v = 2 * c * cloud->points[i_p].y + b * cloud->points[i_p].x + e;
E = 1 + u * u;
F = u * v;
G = 1 + v * v;
double u_v = sqrt(1 + u * u + v * v);
L = (2 * a) / u_v;
M = b / u_v;
N = (2 * c) / u_v;
// 高斯曲率
Gausscurvature = (L * N - M * M) / (E * G - F * F);
Gauss_curvature(i_p, 0) = Gausscurvature;
// 平均曲率
Meancurvature = (E * N - 2 * F * M + G * L) / (2 * E * G - 2 * F * F);
Mean_curvature(i_p, 0) = Meancurvature;
}
}
cout << "高斯曲率为 1:" << Gauss_curvature(1, 0) << endl;
cout << "高斯曲率为 2:" << Gauss_curvature(2, 0) << endl;
cout << "高斯曲率为 40000:" << Gauss_curvature(40000, 0) << endl;
// 显示结果:
boost::shared_ptr viewer(new pcl::visualization::PCLVisualizer("Normal viewer"));
viewer->setBackgroundColor(0.3, 0.3, 0.3); //设置背景颜色
viewer->addText("Curvatures", 10, 10, "text"); //设置显示文字
viewer->setWindowName("Gauss_Mean"); //设置窗口名字
viewer->addCoordinateSystem(0.1); //添加坐标系
//设置点云颜色
pcl::visualization::PointCloudColorHandlerCustom single_color(cloud, 0, 225, 0);
//添加点云到可视化窗口
viewer->addPointCloud(cloud, single_color, "cloud");
//设置点云大小
viewer->setPointCloudRenderingProperties(pcl::visualization::PCL_VISUALIZER_POINT_SIZE, 1, "cloud");
//添加需要显示的点云法向。m_current_cloud为原始点云模型,normal为法向信息,20表示需要显示法向的点云间隔,即每20个点显示一次法向,2表示法向长度。
viewer->addPointCloud(cloud);
// 添加需要显示的点云主曲率。cloud为原始点云模型,normal为法向信息,pri为点云主曲率,
while (!viewer->wasStopped())
{
viewer->spinOnce(100);
boost::this_thread::sleep(boost::posix_time::microseconds(100000));
}
return 0;
}
#endif