《深度学习--基于python的理论与实现》学习笔记4：第二章感知机
感知机是神经网络（深度学习）的起源算法，要弄懂神经网络，首先要搞清楚什么是感知机
2.1感知机
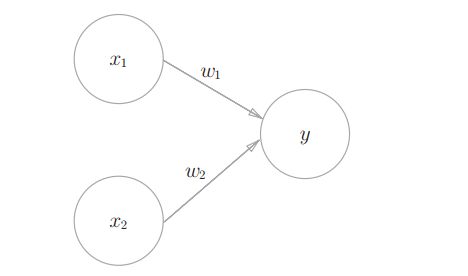
两个输入信号，一个输出信号组成了一种最简单的感知机。输入的信号分别于其权重相乘再求和（x1w1+x2w2），得到的值与一个临界值θ相比，如果比θ大，那么就输出1，也称为“神经元被激活”，如果比θ小，那么输出0。这个临界值也叫作阀值。
将上面的运算通过计算公式表示：
其中x1和x2为输入值，y为输出值，θ为阀值。
如果把 θ左移， θ=-b,那么输入与权重求和之后的值就只需要同零相比：
比零大输出1，比零小输出0，其中b称为偏置。
2.2简单逻辑电路
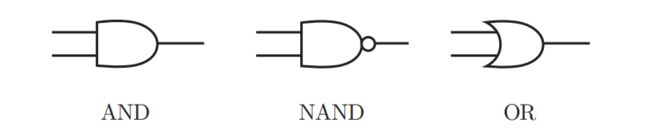
最简单的逻辑电路有：与门，非门，或门，这么我们主要讨论与门，或门和与非门。
- 与门
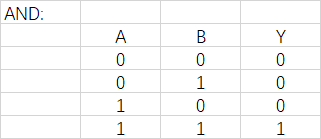
与门：两个输入中，同为1，输出才是1；其他都是0。
- 或门
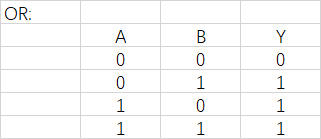
或门：两个输入中，只要存在1，输出就是1。
- 与非门
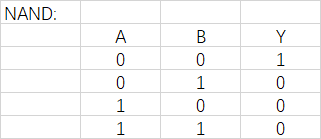
与非门：两个输入中，均为0，输出才是1，其他情况都是0.
- 异或门
图5：异或门的真值表
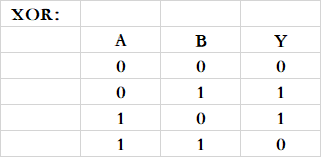
异或门：两个输入中，输入值相同，输出1；输入值不同，输出0。
2.3逻辑电路的功能实现
通过感知机，能够实现与门，或门和与非门的功能，但是不能够实现异或门的功能。
- 与门功能的实现
import numpy as np
def AND(x1,x2):
x=np.array([x1,x2]) #输入
w=np.array([0.5,0.5]) #权重
b=-0.7 #偏置
tmp=np.sum(x*w)+b
if tmp<=0:
return 0
else:
return 1
输出：
>>>AND(0,0)
0
>>>AND(0,1)
0
>>>AND(1,0)
0
>>>AND(1,1)
1
- 或门功能的实现
#或门函数（权重和偏置不同）
def OR(x1,x2):
x=np.array([x1,x2]) #输入
w=np.array([0.5,0.5]) #权重
b=-0.3 #偏置
tmp=np.sum(x*w)+b
if tmp<=0:
return 0
else:
return 1
输出：
>>>OR(0,0)
0
>>>OR(0,1)
1
>>>OR(1,0)
1
>>>OR(1,1)
1
- 与非门功能的实现
def NAND(x1,x2):
x=np.array([x1,x2]) #输入
w=np.array([-0.5,-0.5]) #权重
b=0.7 #偏置
tmp=np.sum(x*w)+b
if tmp<=0:
return 0
else:
return 1
输出：
>>>NAND(0,0)
1
>>>NAND(0,1)
1
>>>NAND(1,0)
1
>>>NAND(1,1)
0
- 异或门功能的实现
异或门不能够通过单层感知机进行实现，因为异或门是一个非线性问题，而前面的与门，或门和与非门均为线性问题
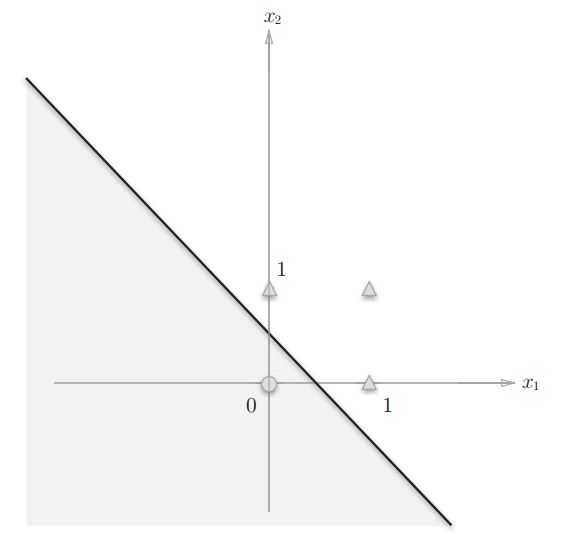
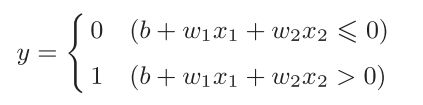
以与非门为例，当输入输出数据显示在坐标轴上时，可以发现，通过一条直线可以把分别属于0和1的部分分割开，如上图的直线所示。用直线所分割的空间称为线性空间
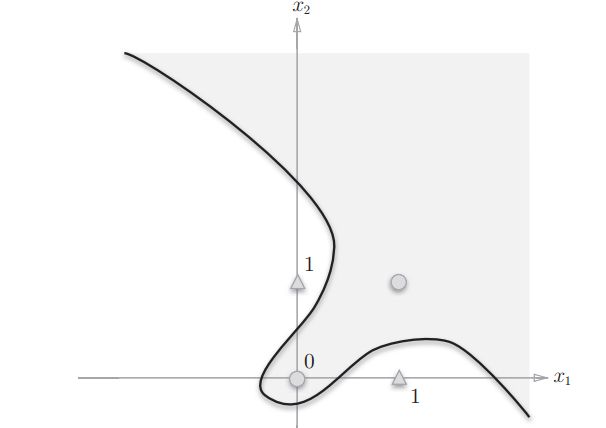
异或门中，0和1的部分不可能通过一条简单的之间进行划分开，只能通过一条曲线进行划分，曲线所分割的空间叫做非线性空间
感知机具有局限性，只能够产生线性空间，不能够产生非线性空间，如果要解决非线性问题，就需要引入多层感知机。
2.4多层感知机
感知机只有一个输入和输出，多层感知机就是在输入和输出之间曾经若干个神经元层，增加模型的复杂度，使其能够产生非线性空间。
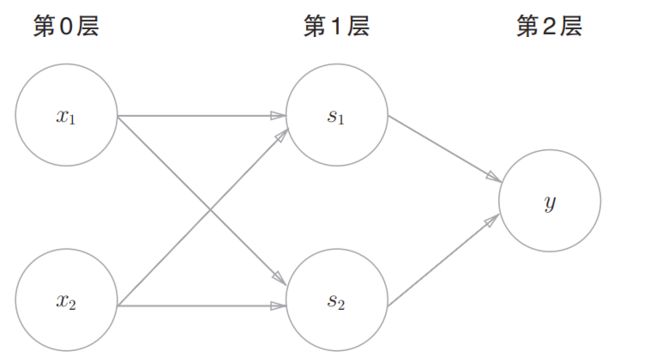
在逻辑电路中，异或门通常是由其他简单的门组合实现的；感知机(单层）能够实现简单门电路的功能，那么多层感知机也就能够实现门电路组合的功能，即能够实现异或门电路的功能。
- 多层感知机实现异或门功能
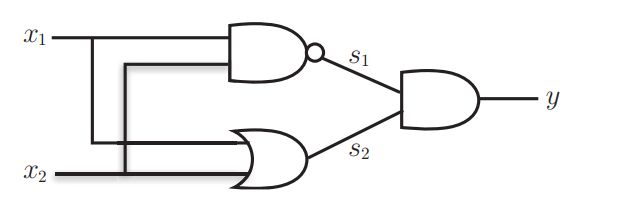
通过与门，与非门和或门的组合，能够实现异或门的功能，进而通过多层感知机，能够实现异或门功能。
#或门函数（权重和偏置不同）
def XOR(x1,x2):
t1=NAND(x1,x2)
t2=OR(x1,x2)
tmp=AND(t1,t2)
if tmp<=0:
return 0
else:
return 1
输出：
>>>OR(0,0)
0
>>>OR(0,1)
1
>>>OR(1,0)
1
>>>OR(1,1)
0
2.5从与非门到计算机
在生活中，通过与非门的组合，就能够在线计算机进行的处理；同理，感知机类似于与非门，多层感知机就类似于与非门的组合，通过多层感知机，也能够实现计算机复杂的计算操作。
感知机能够实现线性操作，叠加层的多层感知机能够实现非线性操作，进而实现复杂的计算机运算操作
参考书籍：
1.《深度学习–基于python的理论与实现》