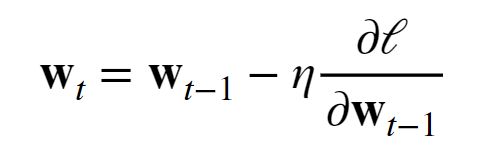深度学习基础11（线性回归使用pytorch里的框架来实现）

线性回归的简洁实现

接下来使用一些框架来实现线性回归学习

框架可以自动化基于梯度的学习算法中重复性的工作。

在上篇文章中，我们只运用了：

（1）通过张量来进行数据存储和线性代数；

（2）通过自动微分来计算梯度。

实际上，由于数据迭代器、损失函数、优化器和神经网络层很常用， 现代深度学习库也为我们实现了这些组件。

下面将介绍如何通过使用深度学习框架来简洁地实现 线性回归模型

生成数据集

与上篇文章类似，首先生成数据集。

import numpy as np
import torch
from torch.utils import data #从torch的utils里面调用一些处理数据的模块
from d2l import torch as d2l

true_w = torch.tensor([2, -3.4])
true_b = 4.2
features, labels = d2l.synthetic_data(true_w, true_b, 1000)

读取数据集

我们可以调用框架中现有的API来读取数据。

什么叫API

我们将features和labels作为API的参数传递，并通过数据迭代器指定batch_size。 此外，布尔值is_train表示是否希望数据迭代器对象在每个迭代周期内打乱数据。

来对下面的代码进行解释:

#假设我们已经有features和lables了，我们把它做成一个list（第六行）

#然后把list传到TensorDataset里面(第三行)，会得到一个pytorch的一个dataset（第三行）

#dataset里拿到数据集之后（第三行），然后调用dataloader这个函数（第四行），用处时每次随机挑选b（batch_size）个样本出来，shuffle意思是说要不要随机去打乱这个顺序，is_train，意思是如果是train的话是需要打乱的

def load_array(data_arrays, batch_size, is_train=True):  #@save
    """构造一个PyTorch数据迭代器"""
    dataset = data.TensorDataset(*data_arrays)
    return data.DataLoader(dataset, batch_size, shuffle=is_train)

batch_size = 10
data_iter = load_array((features, labels), batch_size)#构造一个data_iter

使用data_iter的方式与我们在上篇文章中使用data_iter函数的方式相同。

为了验证是否正常工作，让我们读取并打印第一个小批量样本。

与上篇文章不同，这里使用iter构造Python迭代器，并使用next从迭代器中获取第一项。

next(iter(data_iter))#构造data_iter之后，iter（data_iter）转成一个python的iter，再通过next这个函数来得到一个x和y

[tensor([[-1.4558, -1.2504],

​ [-1.1614, -1.6004],

​ [-0.8811, 0.1561],

​ [ 1.6214, -0.2650],

​ [-0.4122, 1.1322],

​ [-0.1505, 0.1317],

​ [-0.3841, 1.0279],

​ [ 1.4833, -0.6834],

​ [ 0.2704, 0.4626],

​ [-2.5614, 1.3394]]),

tensor([[ 5.5458],

​ [ 7.3117],

​ [ 1.9239],

​ [ 8.3484],

​ [-0.4729],

​ [ 3.4485],

​ [-0.0733],

​ [ 9.4889],

​ [ 3.1777],

​ [-5.4743]])]

定义模型

当我们在上篇文章中实现线性回归时， 我们明确定义了模型参数变量，并编写了计算的代码，这样通过基本的线性代数运算得到输出。 但是，如果模型变得更加复杂，且当你几乎每天都需要实现模型时，你会想简化这个过程。

对于标准深度学习模型，我们可以使用框架的预定义好的层。

这使我们只需关注使用哪些层来构造模型，而不必关注层的实现细节。

我们首先定义一个模型变量net，它是一个Sequential类的实例。 Sequential类将多个层串联在一起。

当给定输入数据时，Sequential实例将数据传入到第一层， 然后将第一层的输出作为第二层的输入，以此类推。

在下面的例子中，我们的模型只包含一个层，因此实际上不需要Sequential。

但是由于以后几乎所有的模型都是多层的，在这里使用Sequential会让你熟悉“标准的流水线”。

这一单层被称为全连接层（fully-connected layer）， 因为它的每一个输入都通过矩阵-向量乘法得到它的每个输出。

在PyTorch中，全连接层在Linear类中定义。 值得注意的是，我们将两个参数传递到nn.Linear中。

• 第一个指定输入特征形状，即2，
• 第二个指定输出特征形状，输出特征形状为单个标量，因此为1。

# nn是神经网络的缩写  Neural Network
from torch import nn
#线性回归是简单的单层神经网络，linear层也就是全连接层
net = nn.Sequential(nn.Linear(2, 1))#指定输入的维度是2，输出的维度是1，但是为了以后的学习更多神经网络，我们把它放到Sequential中，可以理解为list of layers

初始化模型参数

在使用net之前，我们需要初始化模型参数。 如在线性回归模型中的权重和偏置。

深度学习框架通常有预定义的方法来初始化参数。

在这里，我们指定每个权重参数应该从均值为0、标准差为0.01的正态分布中随机采样， 偏置参数将初始化为零。

正如我们在构造nn.Linear时指定输入和输出尺寸一样， 现在我们能直接访问参数以设定它们的初始值。

通过net[0]选择网络中的第一个图层， 然后使用weight.data和bias.data方法访问参数。

我们还可以使用替换方法normal_和fill_来重写参数值。

net[0].weight.data.normal_(0, 0.01)#通过wight来访问w，data里面就是它的真实data，normal_意思是使用正态分布来替换掉data的值，均值为0，标准差为0.01
net[0].bias.data.fill_(0)#bias就是偏差的意思，这里直接设成0

tensor([0.])

定义损失函数

计算均方误差使用的是MSELoss类，也称为平方2范数。 默认情况下，它返回所有样本损失的平均值。

loss = nn.MSELoss()

定义优化算法

SGD：stochastic gradient descent 随机梯度下降

小批量随机梯度下降算法是一种优化神经网络的标准工具， PyTorch在optim模块中实现了该算法的许多变种。

当我们(实例化一个SGD实例)时，我们要指定优化的参数 （可通过net.parameters()从我们的模型中获得）以及优化算法所需的超参数字典。

小批量随机梯度下降只需要设置lr值，这里设置为0.03。

trainer = torch.optim.SGD(net.parameters(), lr=0.03)#SGD需要至少传入两个参数第一个是所有net里面所有参数，包括了w和b，第二个就是需要指定学习率

训练

通过深度学习框架的高级API来实现模型只需要相对较少的代码。

不必单独分配参数、不必定义损失函数，也不必手动实现小批量随机梯度下降。

当我们需要更复杂的模型时，高级API的优势将大大增加。 当我们有了所有的基本组件，训练过程代码与我们从零开始实现时所做的非常相似。

回顾一下：在每个迭代周期里，我们将完整遍历一次数据集（train_data）， 不停地从中获取一个小批量的输入和相应的标签。 对于每一个小批量，我们会进行以下步骤:

• 通过调用net(X)生成预测并计算损失l（前向传播）。
• 通过进行反向传播来计算梯度。
• 通过调用优化器来更新模型参数。
• 反向传播与前向传播的区别详情

为了更好的衡量训练效果，我们计算每个迭代周期后的损失，并打印它来监控训练过程。

num_epochs = 3
for epoch in range(num_epochs):
    for X, y in data_iter:
        l = loss(net(X) ,y)#拿到预测值跟真实的值y做loss
        trainer.zero_grad()#trainer训练器来把梯度清0
        l.backward()#梯度清0后来计算backward梯度，注意这里pytorch以及帮你做了sum了，所以就不用sum了
        #上篇文章这里是l.sum().backward()
        trainer.step()#有了梯度之后，调用step这个函数了来对参数进行更新
    l = loss(net(features), labels)
    print(f'epoch {epoch + 1}, loss {l:f}')

epoch 1, loss 0.000187

epoch 2, loss 0.000106

epoch 3, loss 0.000105

下面比较生成数据集的真实参数和通过有限数据训练获得的模型参数

要访问参数，我们首先从net访问所需的层，然后读取该层的权重和偏置。

正如在上篇文章中实现一样，我们估计得到的参数与生成数据的真实参数非常接近。

w = net[0].weight.data
print('w的估计误差：', true_w - w.reshape(true_w.shape))
b = net[0].bias.data
print('b的估计误差：', true_b - b)

w的估计误差： tensor([0.0002, 0.0008])

b的估计误差： tensor([0.0001])

小结

• 我们可以使用PyTorch的高级API更简洁地实现模型。
• 在PyTorch中，data模块提供了数据处理工具，nn模块定义了大量的神经网络层和常见损失函数。
• 我们可以通过_结尾的方法将参数替换，从而初始化参数。

问题总结

一 为什么loss要求平均

当然我们可以不求平均，那为什么我们要求平均呢？

如上图，loss就是分子，不求平均的话要想让这个数值差不多大的话，前面的学习率就要除以n，那么这样的话，在后面训练调参数的时候，学习率的大小不好调，所以除以n的好处是说不管你的样本有多大，批量多大，我梯度的值都差不多，这样调学习率的时候比较好调。但如果loss不求平均的话，你记得把你的lr除以n就行了

二 batch_size是否会影响最终模型的结果？

在计算次数相同的条件下，batch_size越小，实际上对收敛越好，你不要觉得每次特别小批量会使得噪音影响比较大，对神经网络来说，噪音是一件好事情，因为现在的神经网络太复杂了，一定的噪音使得你不会走偏，就是泛化性更好

三 过拟合和欠拟合情况下，学习率和批次如何调整？

理论上来讲，你的学习率和批量大小不会影响到最后一个收敛结果，但实际上我们一般不能完全求解，所以会有一定影响，但没有太大的影响

四 每次都是随机去除一部分，怎么保证所有的数据都拿过了？

我们这个实现是会保证所有数据都会拿过的

五 如果样本大小不是批量数的整数倍，那么需要随机剔除多余样本吗？

有三种常见做法

• 第一种是最后就拿那些少一点的样本

• 第二种是把最后一个不完整的丢掉

• 第三种是把下一个epoch里面缺多少补多少过来

  ​

六 本质上我们为什么要用SGD

因为大部分实际的loss太复杂，推导不出倒数为0的解，只能逐个batch去逼近

七 backward（）就是调用的back propogation求导