SEMI-SUPERVISED CLASSIFICATION WITH GRAPH CONVOLUTIONAL NETWORKS 论文/GCN学习笔记
1 前置知识:卷积与CNN
该内容在论文中并没有涉及,但理解卷积和CNN对于GCN的理解有帮助,因为GCN是将CNN推广到新的数据结构:graph上面。
1.1与1.2的内容均来自视频:https://www.bilibili.com/video/BV1VV411478E/?spm_id_from=333.880.my_history.page.click&vd_source=9e34c29511733195fced9735e60f8683
1.1 卷积
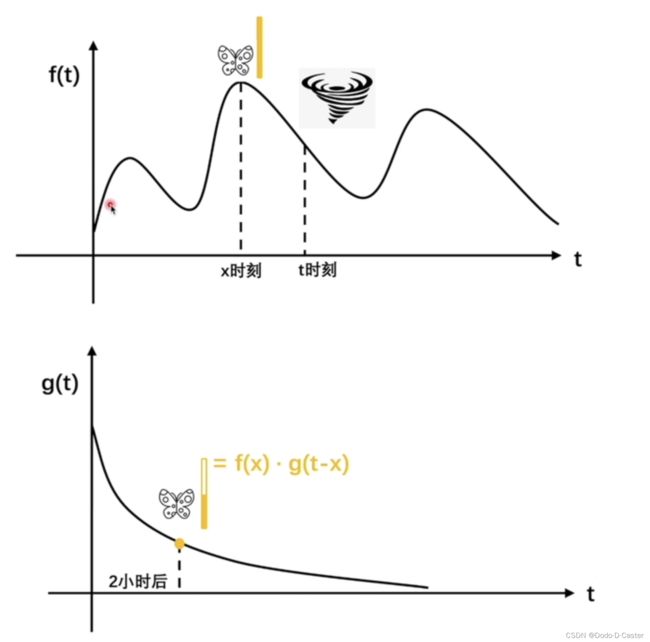
卷积公式: ∫ 0 t f ( x ) g ( t − x ) d x \int _0^t f(x)g(t-x)dx ∫0tf(x)g(t−x)dx
f ( x ) f(x) f(x):在每一个时刻 x x x,都有 f ( x ) f(x) f(x)个蝴蝶煽动翅膀,如3
g ( y ) g(y) g(y):在一个蝴蝶煽动翅膀后, y y y时刻后,该蝴蝶煽动翅膀对引起飓风对影响为 g ( y ) g(y) g(y),如0.5
则在 x x x时刻的3只蝴蝶,经过了 y y y时刻,对 x + y x+y x+y时刻引起飓风的影响为 3 × 0.5 = 1.5 3 \times 0.5 = 1.5 3×0.5=1.5
假设t时刻发生了飓风,求 0 ~ t 0~t 0~t 时刻蝴蝶煽动翅膀对飓风的影响,则有公式: ∫ 0 t f ( x ) g ( t − x ) d x \int _0^t f(x)g(t-x)dx ∫0tf(x)g(t−x)dxy由此我们可以得到该问题中卷积的本质:累加过去对现在的影响
1.2 CNN
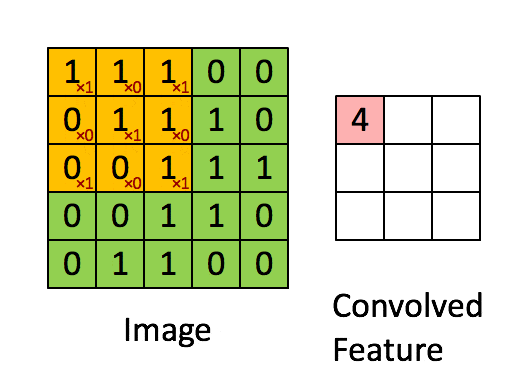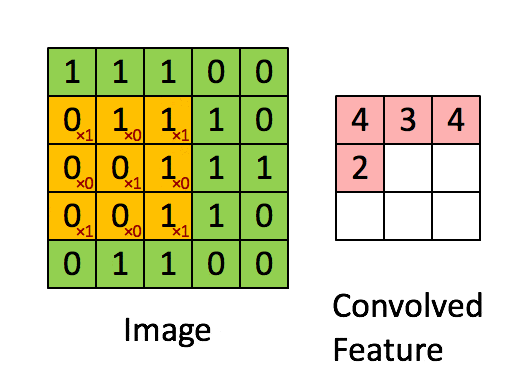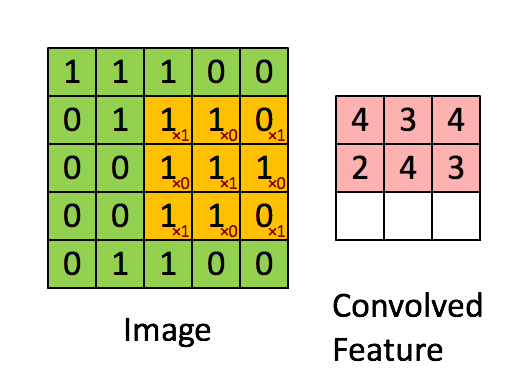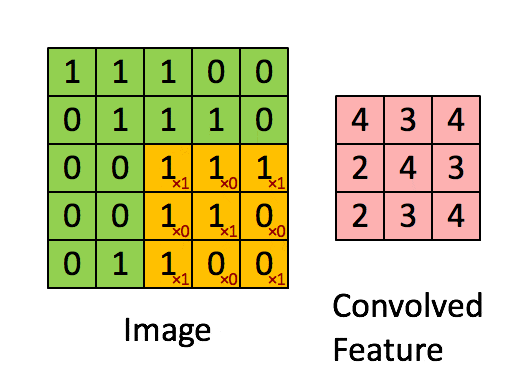
选取不同的卷积核,用卷积核乘3*3的像素矩阵做卷积,可以得到新的像素点,对图中所有的像素矩阵乘卷积核则可以得到新的图像。
其本质是:累加3*3个像素对目标像素的影响,得到目标像素。
1.3 CNN→GCN
由于graph不同于image,没有固定的结构,邻居的数量亦不相同,故将CNN推广到graph上时,GCN将对像素的卷积操作变成了对节点邻居的卷积操作,累加不同邻居对目标节点的影响,得到新的特征。
2 GCN的数学理论
2.1 图谱卷积公式(K阶近似)
graph上的谱卷积公式:
g θ ⋆ x = U g θ U T x g_{\theta} \star x = U g_{\theta} U^T x gθ⋆x=UgθUTx
- g θ g_{\theta} gθ:过滤器,可以理解为对特征值的函数
- x x x:信号,可以理解为每个节点的特征信息
- L = I N − D − 1 2 A D − 1 2 = U Λ U T L=I_N-D^{-\frac{1}{2}}AD^{-\frac{1}{2}}=U \Lambda U^T L=IN−D−21AD−21=UΛUT
- L L L:标准化的图拉普拉斯矩阵
- Λ \Lambda Λ :特征值矩阵
- U T x U^T x UTx:对 x x x进行图傅里叶变换
由于上式特征矩阵的乘法复杂度为 O ( N 2 ) O(N^2) O(N2),并且对于large graph是 L L L进行特征分解同样在计算上消耗巨大,所以要对 g θ ( Λ ) g_{\theta}(\Lambda) gθ(Λ)用切比雪夫多项式(Chebyshev polynomials)进行K阶近似:
g θ ′ ( Λ ) ≈ ∑ k = 0 K θ k ′ T k ( Λ ~ ) g_{\theta '}(\Lambda) ≈ \sum_{k=0}^{K}\theta ' _k T_k (\widetilde \Lambda) gθ′(Λ)≈k=0∑Kθk′Tk(Λ )
- Λ ~ = 2 λ m a x Λ − I N \widetilde \Lambda = \frac{2}{\lambda_{max}}\Lambda - I_N Λ =λmax2Λ−IN
- λ m a x \lambda_{max} λmax:代表图拉普拉斯矩阵的最大特征值
- θ ′ \theta ' θ′:切比雪夫系数向量
- T k ( x ) = 2 x T k − 1 ( x ) − T k − 2 ( x ) , T 0 ( x ) = 1 , T 1 ( x ) = x T_k(x)=2xT_{k-1}(x)-T_{k-2}(x),T_0(x)=1,T_1(x)=x Tk(x)=2xTk−1(x)−Tk−2(x),T0(x)=1,T1(x)=x:切比雪夫多项式的递归定义
结合两个式子,得到总的谱图公式(复杂度为 O ( ∣ E ∣ ) O(|\mathcal{E}|) O(∣E∣),其中 E \mathcal{E} E为边的数量):
g θ ⋆ x ≈ ∑ k = 0 K θ k ′ T k ( L ~ ) x g_{\theta} \star x ≈ \sum_{k=0}^{K}\theta ' _k T_k (\widetilde L)x gθ⋆x≈k=0∑Kθk′Tk(L )x
- L ~ = 2 λ m a x L − I N \widetilde L = \frac{2}{\lambda_{max}}L - I_N L =λmax2L−IN
2.2 Layer-wise线性模型
设定参数:
- K = 1 K=1 K=1:也就是切比雪夫采用1阶近似,此时我们可以得到一个线性的公式
- λ m a x ≈ 2 \lambda _{max} \approx 2 λmax≈2:神经网络的参数会在训练的过程中适应这个改变。
这样,我们可以得到简化后的一阶近似线性公式:
g θ ⋆ x ≈ θ 0 ′ x + θ 1 ′ ( L − I N ) x = θ 0 ′ x − θ 1 ′ D − 1 2 A D − 1 2 x g_{\theta} \star x ≈ \theta_0'x + \theta_1'(L-I_N)x = \theta_0'x - \theta_1'D^{-\frac{1}{2}}AD^{-\frac{1}{2}}x gθ⋆x≈θ0′x+θ1′(L−IN)x=θ0′x−θ1′D−21AD−21x
- θ 0 ′ , θ 1 ′ \theta_0',\theta_1' θ0′,θ1′:全图共享的两个参数
通过限制参数数量来处理过拟合和减少每一层的计算量(如矩阵乘法),得到以下公式:
g θ ⋆ x ≈ θ ( I N + D − 1 2 A D − 1 2 ) x g_{\theta} \star x ≈ \theta(I_N+D^{-\frac{1}{2}}AD^{-\frac{1}{2}})x gθ⋆x≈θ(IN+D−21AD−21)x
- θ = θ 0 ′ = − θ 1 ′ \theta = \theta'_0 = - \theta'_1 θ=θ0′=−θ1′
由于此时 I N + D − 1 2 A D − 1 2 I_N+D^{-\frac{1}{2}}AD^{-\frac{1}{2}} IN+D−21AD−21的特征值取值范围为 [ 0 , 2 ] [0,2] [0,2],重复应用这种计算在神经网络中可能会导致数值不稳定和梯度爆炸/消失,所以进行了如下改变(对称规范化):
- I N + D − 1 2 A D − 1 2 = D ~ − 1 2 A ~ D ~ − 1 2 I_N+D^{-\frac{1}{2}}AD^{-\frac{1}{2}} = \widetilde D^{-\frac{1}{2}} \widetilde A \widetilde D^{-\frac{1}{2}} IN+D−21AD−21=D −21A D −21
- A ~ = A + I N \widetilde A = A + I_N A =A+IN
- D ~ i i = ∑ j A ~ i j \widetilde D_{ii} = \sum_j \widetilde A_{ij} D ii=∑jA ij
此时,可以得到新的公式(复杂度为 O ( ∣ E ∣ F C ) O(|\mathcal{E}|FC) O(∣E∣FC),其中 E \mathcal{E} E为边的数量, F F F为过滤器数量(即label的种数), C C C为每个节点的特征数量):
Z = D ~ − 1 2 A ~ D ~ − 1 2 X Θ Z = \widetilde D^{-\frac{1}{2}} \widetilde A \widetilde D^{-\frac{1}{2}} X \Theta Z=D −21A D −21XΘ
- Z ∈ R N × F Z \in R^{N \times F} Z∈RN×F:卷积信号矩阵
- X ∈ R N × C X \in R^{N \times C} X∈RN×C:每个节点有一个C维特征向量,X为N个节点的特征向量组成的矩阵
- Θ ∈ R C × F \Theta \in R^{C \times F} Θ∈RC×F:过滤器的参数矩阵
2.3 GCN层级更新公式
将上面的公式加上激活函数(作用:给模型加入非线性因素,解决线性模型的分类局限),我们可以得到GCN更新下一层节点信息的公式:
H ( l + 1 ) = σ ( D ~ − 1 2 A ~ D ~ − 1 2 H ( l ) W ( l ) ) H^{(l+1)}=σ(\widetilde D^{- \frac{1}{2}} \widetilde A \widetilde D^{- \frac{1}{2}} H^{(l)} W^{(l)} ) H(l+1)=σ(D −21A D −21H(l)W(l))
- H ( l ) H^{(l)} H(l) :图中各节点的特征矩阵(第l层)
- σ ( − ) σ(-) σ(−) :激活函数
- R e L U ( − ) = m a x ( 0. − ) ReLU(-)=max(0.-) ReLU(−)=max(0.−)
- s o f t m a x ( − ) softmax(-) softmax(−)
- W ( l ) W^{(l)} W(l) :可训练的权重矩阵(第l层)
2.4 对称规范化 D ~ − 1 2 A ~ D ~ − 1 2 \widetilde D^{- \frac{1}{2}} \widetilde A \widetilde D^{- \frac{1}{2}} D −21A D −21的物理意义
这一部分并没有出现在论文中,但给出了对称规范化式子处理数值不稳定和梯度爆炸/消失问题以外的更为直观的物理意义 ---- 削弱强邻居的影响
来自视频:https://www.bilibili.com/video/BV1Xy4y1i7sq/?spm_id_from=333.337.search-card.all.click&vd_source=9e34c29511733195fced9735e60f8683
首先, A ~ = A + I \widetilde A = A+I A =A+I的意义是给图上每个节点加上自环,这样在考虑节点邻居信息的同时会考虑节点本身的信息。
其次, D ~ − 1 2 A ~ D ~ − 1 2 \widetilde D^{- \frac{1}{2}} \widetilde A \widetilde D^{- \frac{1}{2}} D −21A D −21可以通过如下过程展开:
( D ~ − 1 2 A ~ D ~ − 1 2 H ) i = ( D ~ − 1 2 A ~ ) i D ~ − 1 2 H = ( ∑ k D ~ i k − 1 2 A ~ i ) D ~ − 1 2 H = D ~ i i − 1 2 ∑ j A ~ i j ∑ k D ~ j k − 1 2 H j = D ~ i i − 1 2 ∑ j A ~ i j D ~ j j − 1 2 H j = ∑ j 1 D ~ i i D ~ j j A ~ i j \begin{align*} (\widetilde D^{- \frac{1}{2}} \widetilde A \widetilde D^{- \frac{1}{2}}H)_i &= (\widetilde D^{- \frac{1}{2}} \widetilde A)_i \widetilde D^{- \frac{1}{2}}H \\ &= (\sum_k \widetilde D^{- \frac{1}{2}}_{ik} \widetilde A_i)\widetilde D^{- \frac{1}{2}}H \\ &= \widetilde D^{- \frac{1}{2}}_{ii} \sum_j \widetilde A_{ij} \sum_k \widetilde D^{- \frac{1}{2}}_{jk}H_j \\ &= \widetilde D^{- \frac{1}{2}}_{ii} \sum_j \widetilde A_{ij} \widetilde D^{- \frac{1}{2}}_{jj}H_j \\ &= \sum_j{\frac{1}{\sqrt{\widetilde D_{ii} \widetilde D_{jj}}} \widetilde A_{ij}} \end{align*} (D −21A D −21H)i=(D −21A )iD −21H=(k∑D ik−21A i)D −21H=D ii−21j∑A ijk∑D jk−21Hj=D ii−21j∑A ijD jj−21Hj=j∑D iiD jj1A ij
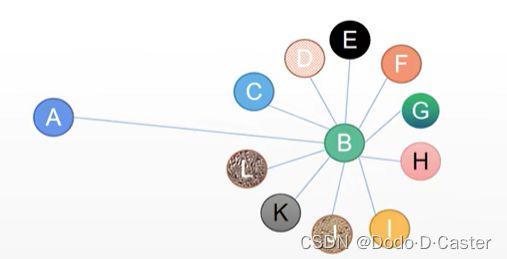
由此,我们得到了等式: D ~ − 1 2 A ~ D ~ − 1 2 = ∑ j 1 D ~ i i D ~ j j A ~ i j \widetilde D^{- \frac{1}{2}} \widetilde A \widetilde D^{- \frac{1}{2}} = \sum_j{\frac{1}{\sqrt{\widetilde D_{ii} \widetilde D_{jj}}} \widetilde A_{ij}} D −21A D −21=∑jD iiD jj1A ij,其意义为:对称规范化后的式子在加权累加节点 i 的邻居的时候,通过除以节点 i 和节点 j 的度的根号次来了削弱强邻居的影响。通过下图可以更好的理解:
在普通的GNN中,A会累加聚合B的信息,但实际A和B的差别很大:B有很多邻居,而A只认识B,显而易见B的影响力不等于A的影响力。GCN通过对称规范化缓减了这个问题,在累加的时候会除以AB度矩阵乘积的根号次来削弱强邻居的影响。
3 半监督节点分类
related work:前人已经对在图上运用神经网络有了尝试,但它们大部分不适用于large graph,或者对节点顺序有要求
作者代码:https://github.com/tkipf/gcn
源码解读:https://www.jianshu.com/p/bb38e9ca6347
简单实现(dgl,与源码方法略有不同,但更易理解):https://towardsdatascience.com/start-with-graph-convolutional-neural-networks-using-dgl-cf9becc570e1
3.1 流程
原文描述:首先使用所有带标签的训练集数据训练一个本地的分类器,并用该本地分类器来指导未标记的节点的分类进行关系分类训练(本文对未标签的节点进行了10次迭代)
个人理解:首先先对所有有标签的数据进行训练,训练的时候会聚合无标签的节点(包括测试集和训练集中无标签的部分),然后再用训练完成的分类器对无标签的节点进行分类。
- 输入层:C维节点的特征,通过 W 0 W_0 W0(维度:C x H)将特征矩阵降维到(节点个数 x H)
- 隐藏层:通过 W 1 W_1 W1(维度:H x F)将特征矩阵降维到(节点个数 x F)
- 输出层:F个feature maps,每一个feature map对应一个分类
- 分类:未标签的节点在F个feature map中feature最大的map即为该节点的类别
- 数据集:Citeseer, Cora, PubMed, NELL
- 层数:2
GCN的计算流程:
- 预处理:
- 归一化特征向量: A = D − 1 A A = D^{-1} A A=D−1A
- 给A加上自环: A ~ = A + I N \widetilde A = A + I_N A =A+IN
- 对称归一化: A ^ = D ~ − 1 2 A ~ D ~ − 1 2 \hat A = \widetilde D^{-\frac{1}{2}} \widetilde A \widetilde D^{-\frac{1}{2}} A^=D −21A D −21
- 聚合更新:
- Z = f ( X , A ) = s o f t m a x ( A ~ R e L U ( A ~ X W ( 0 ) ) W ( 1 ) ) Z = f(X,A) = softmax(\widetilde A ReLU(\widetilde A X W^{(0)})W^{(1)}) Z=f(X,A)=softmax(A ReLU(A XW(0))W(1))
- 激活函数: s o f t m a x ( x i ) = 1 z e x p ( x i ) softmax(x_i)=\frac{1}{z}exp(x_i) softmax(xi)=z1exp(xi), z = ∑ i e x p ( x i ) z=\sum_iexp(x_i) z=∑iexp(xi)
- 神经网络权重: W ( 0 ) , W ( 1 ) W^{(0)},W^{(1)} W(0),W(1) → 由梯度下降法训练得到
- 损失函数:
- 交叉熵误差: L = − ∑ l ∈ y L ∑ f = 1 F Y l f l n Z l f L=-\sum_{l \in y_L} \sum_{f=1}^F Y_{lf}lnZ_{lf} L=−∑l∈yL∑f=1FYlflnZlf
- y L y_L yL:具有标签的节点索引集
作者在文章的开始指名其他方法的loss设计如下:(该方法需要假设连接的节点倾向于拥有相同的标签,但实际上存在边不能代表两个节点具有相似性)
L = L o + λ L r e g L = L_o + \lambda L_{reg} L=Lo+λLreg
- L 0 L_0 L0 代表全监督训练的loss
- 图拉普拉斯规范化项: L r e g = ∑ i , j ∣ ∣ f ( X i ) − f ( X j ) ∣ ∣ 2 = f ( X ) T ∆ f ( X ) L_{reg} = \sum_{i,j} || f(X_i)-f(X_j) ||^2 = f(X)^T ∆ f(X) Lreg=∑i,j∣∣f(Xi)−f(Xj)∣∣2=f(X)T∆f(X)
超参数的设定:
- 对于Citeseer, Cora, PubMed : dropout rate (0.5), L2 regularization ( 5 × 1 0 − 4 5 \times 10^{-4} 5×10−4), number of hidden units (16)
- 对于NELL : dropout rate (0.1), L2 regularization ( 1 × 1 0 − 5 1 \times 10^{-5} 1×10−5), number of hidden units (64)
- 其中,dropout rate用于所有层,L2 regularization只用在第一层
3.2 结果:
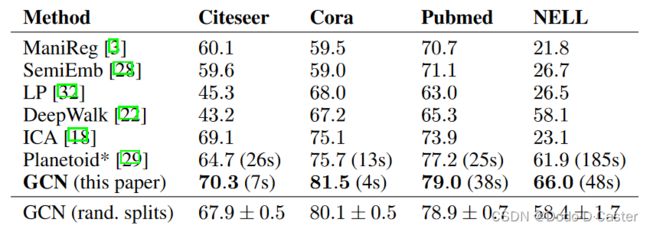
不同模型的准确率对比:
不同传播方法的准确率对比:
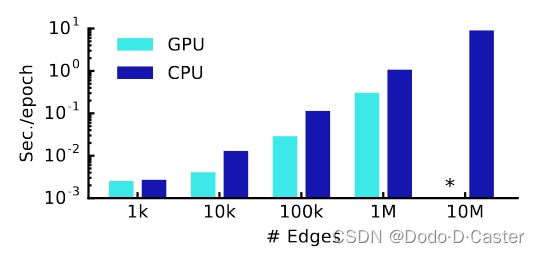
GPU vs CPU
3.3 对比
- 基于图拉普拉斯规范化的方法
- 局限:需要假设存在边的两节点相似,也就是倾向于具有相同的标签 (本文3.1 Loss部分有提)
- 基于Skip-gram的方法
- 局限:这些方法基于难以优化的multi-step pipeline
- 本文的方法
- 优点:解决了上述的局限
- 局限:
- 无法在GPU上训练large graph — 可能的解决方法:minibatch
- 不支持边的特征,局限于无向图 — 可能的解决方法:加入代表边特征的节点
- 没有权衡参数 λ \lambda λ - A ~ = A + λ I N \tilde A = A + \lambda I_N A~=A+λIN — 可能的解决方法:使用梯度下降来学习
4 个人产生的疑问
4.1 GNN中transductive和inductive learning的区别
疑问来源: 在梳理GCN的时候,对GCN如何做分类产生了疑问。在训练的时候邻接矩阵中包含了所有节点(包括训练集和测试集)的信息,那么在训练的过程中,训练集中的未标签数据和测试集的数据是不是起到了一样的作用?
解答:
https://blog.csdn.net/u012762410/article/details/127213748
https://datascience.stackexchange.com/questions/73654/what-is-difference-between-transductive-and-inductive-in-gnn
GNN中transductive和inductive learning
- 相同点:输入都是whole graph
- 不同点:
- 对于transductive,训练时测试集的节点是可知的,可以用测试集中的节点的除了标签以外的全部信息
- 对于inductive,训练时测试集的节点是不可知的,不能使用测试集中的节点的任何信息
GCN是transductive learning。在正向传播的过程中,会训练所有节点(包括训练集中的未标签数据和测试集)的特征,而在反向传播的时候,对于第二层网络,会用带标签的节点计算loss进行反向传播,对于第一层网络,则不用关注标签的问题,用后一层传播来的数据进行计算即可。