线性回归模型公式推导
线性回归公式推导
- 线性模型
- 一、线性回归
-
- (一)一元线性回归
-
- 1. 由最小二乘法得出损失函数
- 2. 证明损失函数 E ( w , b ) E(w,b) E(w,b)是关于 w w w和 b b b的凸函数
- 3. 对损失函数求关于b和w的一阶偏导数
- 4. 令一阶偏导数为0解出 w w w和 b b b
- (二)多元线性回归
-
- 1. 由最小二乘法求出损失函数
- 2. 证明损失函数 E w ^ E_{\hat w} Ew^是关于 w ^ \hat w w^的凸函数
- 3. 令一阶偏导数为0,解出 w ^ \hat w w^
- 二、对数几率回归
-
- (一)广义线性模型
- (二)对数几率回归公式推导
-
- 1. 对数几率回归模型
- 2. 极大似然估计方法
本内容依据周志华老师的《机器学习》(西瓜书)总结而来。初次发文,若有不当的地方,还请指正。
线性模型
给定有 d d d个属性描述的示例 x = ( x 1 ; x 2 ; . . . ; x d ) x=(x_1;x_2;...;x_d) x=(x1;x2;...;xd),其中 x i x_i xi是 x x x在第 i i i个属性上的取值,线性模型(linear model)试图学得一个通过属性的线性组合来进行预测的函数,即 f ( x ) = w 1 x 1 + w 2 x 2 + . . . + w d x d + b f(x)=w_1x_1+w_2x_2+...+w_dx_d+b f(x)=w1x1+w2x2+...+wdxd+b一般用向量的形式写成 f ( x ) = w T x + b f(x)=w^Tx+b f(x)=wTx+b其中 w = ( w 1 ; w 2 ; . . . ; w d ) w =(w_1;w_2;...;w_d) w=(w1;w2;...;wd) w w w和 b b b学得之后,模型就得以确定。
线性模型形式简单、易于建模,但蕴含着机器学习中的一些重要的基本思想。许多功能更为强大的非线性模型(nonlinear model)可在线性模型的基础上通过引入层级结构或高维映射而得。
一、线性回归
(一)一元线性回归
在线性回归问题中,首先考虑输入属性的数目只有一个,即一元线性回归问题,试图学得 f ( x i ) = w x i + b , 使 得 f ( x i ) ≃ y i f(x_i)=wx_i+b,使得f(x_i)\simeq y_i f(xi)=wxi+b,使得f(xi)≃yi
求解步骤:
1. 由最小二乘法得出损失函数E(w,b)
2. 证明损失函数E(w,b)是关于w和b的凸函数
3. 对损失函数求关于b和w的一阶偏导数
4. 令一阶偏导数等于0,解出w和b
1. 由最小二乘法得出损失函数
E ( w , b ) = ∑ i = 1 m ( y i − f ( x i ) ) 2 = ∑ i = 1 m ( y i − w x i − b ) 2 \begin{aligned}E_{(w,b)}&=\sum^m_{i=1}(y_i-f(x_i))^2\\ &=\sum_{i=1}^m (y_i-wx_i-b)^2\end{aligned} E(w,b)=i=1∑m(yi−f(xi))2=i=1∑m(yi−wxi−b)2均方误差有非常好的几何意义,它对应了常用的欧几里得距离或简称“欧氏距离”(Euclidean distance)。基于均方误差最小化来进行模型求解的方法称为“最小二乘法”(least square method)。在线性回归中,最小二乘法就是试图找到一条直线,使所有样本到直线上的欧氏距离之和最小。即求解目的为: ( w , b ) = arg min ( w , b ) ∑ i = 1 m ( y i − w x i − b ) 2 (w,b)=\mathop{\arg\min}\limits_{(w,b)}\sum^m_{i=1}(y_i-wx_i-b)^2 (w,b)=(w,b)argmini=1∑m(yi−wxi−b)2
2. 证明损失函数 E ( w , b ) E(w,b) E(w,b)是关于 w w w和 b b b的凸函数
二元函数判断凹凸性:
设 f ( x , y ) f(x,y) f(x,y)在区域D上具有二阶连续偏导数,记 A = f x x ′ ′ ( x , y ) , B = f x y ′ ′ ( x , y ) , C = f y y ′ ′ ( x , y ) A=f^{''}_{xx}(x,y), B=f^{''}_{xy}(x,y), C=f^{''}_{yy}(x,y) A=fxx′′(x,y),B=fxy′′(x,y),C=fyy′′(x,y)
(1) 在D上恒有A>0,且 A C − B 2 > = 0 AC-B^2>=0 AC−B2>=0时, f ( x , y ) f(x,y) f(x,y)在区域D上是凸函数;
(2) 在D上恒有A<0,且 A C − B 2 > = 0 AC-B^2>=0 AC−B2>=0时, f ( x , y ) f(x,y) f(x,y)在区域D上是凹函数。
二元凹凸函数求最值:
设 f ( x , y ) f(x,y) f(x,y)是在开区域D内具有连续偏导数的凸(或者凹)函数 ( x 0 , y 0 ) ∈ D (x_0,y_0)\in D (x0,y0)∈D,且 f x ′ ( x 0 , y 0 ) = 0 , f y ′ ( x 0 , y 0 ) = 0 f^{'}_{x}(x_0,y_0)=0,f^{'}_{y}(x_0,y_0)=0 fx′(x0,y0)=0,fy′(x0,y0)=0,则 f ( x 0 , y 0 ) f(x_0,y_0) f(x0,y0)必为 f ( x , y ) f(x,y) f(x,y)在D内的最小值(或最大值)。
求 A = f x x ′ ′ ( x , y ) A=f^{''}_{xx}(x,y) A=fxx′′(x,y):
∂ E ( w , b ) ∂ w = ∂ ∂ w [ ∑ i = 1 m ( y i − w x i − b ) 2 ] = 2 ∑ i = 1 m x i ( b + w x i − y i ) ∂ 2 E ( w , b ) ∂ w 2 = ∂ ∂ w ( ∂ E ( w , b ) ∂ w ) = 2 ∑ i = 1 m x i 2 \begin{aligned}{\partial E_{(w,b)}\over\partial w}&={\partial\over \partial w}[\sum ^m_{i=1}(y_i-wx_i-b)^2]\\ &=2\sum_{i=1}^mx_i(b+wx_i-y_i)\\ {\partial ^2E_{(w,b)}\over\partial w^2}&={\partial \over\partial w}({\partial{E_{(w,b)}}\over\partial w})\\&=2\sum ^m_{i=1}x_i^2 \end{aligned} ∂w∂E(w,b)∂w2∂2E(w,b)=∂w∂[i=1∑m(yi−wxi−b)2]=2i=1∑mxi(b+wxi−yi)=∂w∂(∂w∂E(w,b))=2i=1∑mxi2此即为 A = f x x ′ ′ ( x , y ) A=f^{''}_{xx}(x,y) A=fxx′′(x,y)。
求 B = f x y ′ ′ ( x , y ) B=f^{''}_{xy}(x,y) B=fxy′′(x,y):
∂ 2 E ( w , b ) ∂ w ∂ b = ∂ ∂ b ( ∂ E ( w , b ) ∂ w ) = 2 ∑ i = 1 m x i \begin{aligned} {\partial ^2E_{(w,b)}\over{\partial w\partial b}}&={\partial \over\partial b}({\partial E_{(w,b)}\over\partial w})\\ &=2\sum ^m_{i=1}x_i \end{aligned} ∂w∂b∂2E(w,b)=∂b∂(∂w∂E(w,b))=2i=1∑mxi此即为 B = f x y ′ ′ ( x , y ) B=f^{''}_{xy}(x,y) B=fxy′′(x,y)。
求 C = f y y ′ ′ ( x , y ) C=f^{''}_{yy}(x,y) C=fyy′′(x,y):
∂ E ( w , b ) ∂ b = ∂ ∂ b [ ∑ i = 1 m ( y i − w x i − b ) 2 ] = 2 ( m b − ∑ i = 1 m ( y i − w x i ) ) ∂ 2 E ( w , b ) ∂ b 2 = ∂ ∂ b ( ∂ E ( w , b ) ∂ b ) = 2 m \begin{aligned} {\partial E_{(w,b)}\over{\partial b}}&={\partial \over \partial b}[\sum_{i=1}^m(y_i-wx_i-b)^2]\\ &=2(mb-\sum^m_{i=1}(y_i-wx_i))\\ {\partial ^2E_{(w,b)}\over{\partial b^2}}&={\partial \over \partial b}({\partial{E_{(w,b)}}\over\partial b})\\ &=2m \end{aligned} ∂b∂E(w,b)∂b2∂2E(w,b)=∂b∂[i=1∑m(yi−wxi−b)2]=2(mb−i=1∑m(yi−wxi))=∂b∂(∂b∂E(w,b))=2m此即为 C = f y y ′ ′ ( x , y ) C=f^{''}_{yy}(x,y) C=fyy′′(x,y)。
易知 A > 0 , A C − B 2 = 4 m ∑ i = 1 m ( x i − x ‾ ) 2 > = 0 A>0,AC-B^2=4m\sum_{i=1}^m(x_i-\overline x)^2>=0 A>0,AC−B2=4m∑i=1m(xi−x)2>=0,故损失函数 E ( w , b ) E(w,b) E(w,b)是关于 w w w和 b b b的凸函数得证。
3. 对损失函数求关于b和w的一阶偏导数
∂ E ( w , b ) ∂ b = 2 ( m b − ∑ i = 1 m ( y i − w x i ) ) ∂ E ( w , b ) ∂ w = 2 ∑ i = 1 m x i ( b + w x i − y i ) \begin{aligned} {\partial E_{(w,b)}\over{\partial b}}&=2(mb-\sum^m_{i=1}(y_i-wx_i))\\ {\partial E_{(w,b)}\over\partial w} &=2\sum_{i=1}^mx_i(b+wx_i-y_i) \end{aligned} ∂b∂E(w,b)∂w∂E(w,b)=2(mb−i=1∑m(yi−wxi))=2i=1∑mxi(b+wxi−yi)
4. 令一阶偏导数为0解出 w w w和 b b b
{ ∂ E ( w , b ) ∂ b = 2 [ m b − ∑ i = 1 m ( y i − w x i ) ] = 0 ∂ E ( w , b ) ∂ w = 2 ∑ i = 1 m x i ( b + w x i − y i ) = 0 \begin{cases} {\partial E_{(w,b)}\over{\partial b}}&=2[mb-\sum^m_{i=1}(y_i-wx_i)]=0\\ {\partial E_{(w,b)}\over\partial w}&=2\sum_{i=1}^mx_i(b+wx_i-y_i)=0 \end{cases} {∂b∂E(w,b)∂w∂E(w,b)=2[mb−∑i=1m(yi−wxi)]=0=2∑i=1mxi(b+wxi−yi)=0得:
b = 1 m ∑ i = 1 m ( y i = w x i ) = 1 m ∑ i = 1 m y i − w ⋅ 1 m ∑ i = 1 m x i = y ‾ − w x ‾ w = ∑ i = 1 m y i x i − y ‾ ∑ i = 1 m x i ∑ i = 1 m x i 2 − x ‾ ∑ i = 1 m x i \begin{aligned} b&={1\over m}\sum^m_{i=1}(y_i=wx_i)\\ &={1\over m}\sum_{i=1}^my_i-w\cdot{1\over m}\sum_{i=1}^mx_i\\ &=\overline y-w\overline x\\ w=&{{\sum^m_{i=1}y_ix_i-\overline y\sum_{i=1}^mx_i}\over{\sum_{i=1}^mx_i^2-\overline x\sum_{i=1}^mx_i}} \end{aligned} bw==m1i=1∑m(yi=wxi)=m1i=1∑myi−w⋅m1i=1∑mxi=y−wx∑i=1mxi2−x∑i=1mxi∑i=1myixi−y∑i=1mxi至此,便求出了一元线性模型的参数 w w w和 b b b。
(二)多元线性回归
由一元的情况扩展开来,此时样本由d个属性描述,此时我们试图学得 f ( x i ) = w T x i + b , 使 得 f ( x i ) ≃ y i f(x_i)=w^Tx_i+b,使得f(x_i)\simeq y_i f(xi)=wTxi+b,使得f(xi)≃yi即多元线性回归问题,求解步骤与一元线性回归模型相似。
1. 由最小二乘法求出损失函数
f ( x i ) = w T x i + b = ( w 1 , w 2 , . . . , w d ) ( x i 1 x i 2 . . . x i d ) + b = b 记 作 w d + 1 ( w 1 , w 2 , . . . , w d , w d + 1 ) ( x i 1 x i 2 ⋮ x i d 1 ) = w ^ T x ^ i \begin{aligned} f(x_i)&=w^Tx_i+b\\ &=(w_1,w_2,...,w_d) \begin{pmatrix} x_{i1}\\x_{i2}\\...\\x_{id} \end{pmatrix}+b\\ &\overset{b记作w_{d+1}}{=}(w_1,w_2,...,w_d,w_{d+1}) \begin{pmatrix} x_{i1}\\x_{i2}\\\vdots\\x_{id}\\1 \end{pmatrix}\\ &=\hat w^T\hat x_i \end{aligned} f(xi)=wTxi+b=(w1,w2,...,wd)⎝⎜⎜⎛xi1xi2...xid⎠⎟⎟⎞+b=b记作wd+1(w1,w2,...,wd,wd+1)⎝⎜⎜⎜⎜⎜⎛xi1xi2⋮xid1⎠⎟⎟⎟⎟⎟⎞=w^Tx^i如此一来,就将回归模型记为 f ( x ^ i ) = w ^ T x ^ i f(\hat x_i)=\hat w^T\hat x_i f(x^i)=w^Tx^i,便于后续的分析。接下来便由最小二乘法定义损失函数:
E w ^ = ∑ i = 1 m ( y i − f ( x ^ i ) ) = ∑ i = 1 m ( y i − w ^ T x ^ i ) 2 \begin{aligned} E_{\hat w}&=\sum_{i=1}^m(y_i-f(\hat x_i))\\ &=\sum_{i=1}^m(y_i-\hat w^T\hat x_i)^2 \end{aligned} Ew^=i=1∑m(yi−f(x^i))=i=1∑m(yi−w^Tx^i)2 为便于分析,可做如下定义:
X = ( x 11 x 12 … x 1 d 1 x 21 x 22 … x 2 d 1 ⋮ ⋮ ⋱ ⋮ ⋮ x m 1 x m 2 … x m d 1 ) = ( x 1 T 1 x 2 T 1 ⋮ ⋮ x m T 1 ) = ( x ^ 1 T x ^ 2 T ⋮ x ^ m T ) y = ( y 1 , y 2 , … , y m ) \begin{aligned} X&=\begin{pmatrix} x_{11}&x_{12}&\dots&x_{1d}&1\\ x_{21}&x_{22}&\dots&x_{2d}&1\\ \vdots&\vdots&\ddots&\vdots&\vdots\\ x_{m1}&x_{m2}&\dots&x_{md}&1 \end{pmatrix}=\begin{pmatrix} x_1^T&1\\ x_2^T&1\\ \vdots&\vdots\\ x_m^T&1 \end{pmatrix}=\begin{pmatrix} \hat x^T_1\\\hat x_2^T\\\vdots\\\hat x_m^T\end{pmatrix}\\\\ y&=(y_1,y_2,\dots,y_m) \end{aligned} Xy=⎝⎜⎜⎜⎛x11x21⋮xm1x12x22⋮xm2……⋱…x1dx2d⋮xmd11⋮1⎠⎟⎟⎟⎞=⎝⎜⎜⎜⎛x1Tx2T⋮xmT11⋮1⎠⎟⎟⎟⎞=⎝⎜⎜⎜⎛x^1Tx^2T⋮x^mT⎠⎟⎟⎟⎞=(y1,y2,…,ym) 如此一来,可得:
( y 1 − w ^ T x ^ 1 y 2 − w ^ T x ^ 2 ⋮ y m − w ^ T x ^ m ) = ( y 1 y 2 ⋮ y m ) − ( w ^ T x ^ 1 w ^ T x ^ 2 ⋮ w ^ T x ^ m ) = ( y 1 y 2 ⋮ y m ) − ( x ^ 1 T w ^ x ^ 2 T w ^ ⋮ x ^ m T w ^ ) = y − X w ^ \begin{aligned} \begin{pmatrix} y_1-\hat w^T\hat x_1\\ y_2-\hat w^T\hat x_2\\ \vdots\\ y_m-\hat w^T\hat x_m \end{pmatrix} &=\begin{pmatrix} y_1\\y_2\\\vdots\\y_m \end{pmatrix}-\begin{pmatrix} \hat w^T\hat x_1\\ \hat w^T\hat x_2\\ \vdots\\ \hat w^T\hat x_m \end{pmatrix}\\ &=\begin{pmatrix} y_1\\y_2\\\vdots\\y_m \end{pmatrix}-\begin{pmatrix} \hat x_1^T\hat w\\ \hat x_2^T\hat w\\ \vdots\\ \hat x_m^T\hat w \end{pmatrix}\\ &=y-X\hat w \end{aligned} ⎝⎜⎜⎜⎛y1−w^Tx^1y2−w^Tx^2⋮ym−w^Tx^m⎠⎟⎟⎟⎞=⎝⎜⎜⎜⎛y1y2⋮ym⎠⎟⎟⎟⎞−⎝⎜⎜⎜⎛w^Tx^1w^Tx^2⋮w^Tx^m⎠⎟⎟⎟⎞=⎝⎜⎜⎜⎛y1y2⋮ym⎠⎟⎟⎟⎞−⎝⎜⎜⎜⎛x^1Tw^x^2Tw^⋮x^mTw^⎠⎟⎟⎟⎞=y−Xw^故: E w ^ = ( y − X w ^ ) T ( y − X w ^ ) E_{\hat w}=(y-X\hat w)^T(y-X\hat w) Ew^=(y−Xw^)T(y−Xw^)
2. 证明损失函数 E w ^ E_{\hat w} Ew^是关于 w ^ \hat w w^的凸函数
∂ E w ^ ∂ w ^ = ∂ ∂ w ^ [ ( y − X w ^ ) T ( y − X w ^ ) ] = ∂ ∂ w ^ ( y T − w ^ T X T ) ( y − X w ^ ) = ∂ ∂ w ^ ( y T y − w ^ T X T y − y T X w ^ + w ^ T X T X w ^ ) = ∂ ∂ w ^ ( − w ^ T X T y − y T X w ^ + w ^ T X T X w ^ ) = ( − y T X ) T − X T y + ( X T X + X T X ) w ^ = 2 X T ( X w ^ − y ) \begin{aligned} {\partial E_{\hat w}\over \partial\hat w} &={\partial \over {\partial \hat w}}[(y-X\hat w)^T(y-X\hat w)]\\ &={\partial \over {\partial \hat w}}(y^T-\hat w^TX^T)(y-X\hat w)\\ &={\partial \over\partial \hat w}(y^Ty-\hat w^TX^Ty-y^TX\hat w+\hat w^TX^TX\hat w)\\ &={\partial \over\partial \hat w}(-\hat w^TX^Ty-y^TX\hat w+\hat w^TX^TX\hat w)\\ &=(-y^TX)^T-X^Ty+(X^TX+X^TX)\hat w\\ &=2X^T(X\hat w-y) \end{aligned} ∂w^∂Ew^=∂w^∂[(y−Xw^)T(y−Xw^)]=∂w^∂(yT−w^TXT)(y−Xw^)=∂w^∂(yTy−w^TXTy−yTXw^+w^TXTXw^)=∂w^∂(−w^TXTy−yTXw^+w^TXTXw^)=(−yTX)T−XTy+(XTX+XTX)w^=2XT(Xw^−y) 上述式子中用到了矩阵微分公式:
∂ x T a ∂ x = ∂ a T x ∂ x = a , ∂ x T B x ∂ x = ( B + B T ) x {\partial x^Ta \over \partial x}={\partial a^Tx\over\partial x}=a, {\partial x^TBx\over \partial x}=(B+B^T)x ∂x∂xTa=∂x∂aTx=a,∂x∂xTBx=(B+BT)x 继续对 E w ^ E_{\hat w} Ew^求二阶导:
∂ 2 E w ^ ∂ w ^ 2 = ∂ ∂ w ^ [ 2 X T ( X w ^ − y ) ] = ( 2 X T X ) T = 2 X T X \begin{aligned} {\partial^2E_{\hat w}\over\partial\hat w^2}&={\partial\over\partial \hat w}[2X^T(X\hat w-y)]\\ &=(2X^TX)^T\\ &=2X^TX \end{aligned} ∂w^2∂2Ew^=∂w^∂[2XT(Xw^−y)]=(2XTX)T=2XTX 由多元实值函数凹凸性判定定理,若 X T X X^TX XTX是正定矩阵,则 E w ^ E_{\hat w} Ew^为凸函数。
3. 令一阶偏导数为0,解出 w ^ \hat w w^
2 X T ( X w ^ − y ) = 0 得 w ^ = ( X T X ) − 1 X T y 2X^T(X\hat w-y)=0\\得\hat w=(X^TX)^{-1}X^Ty 2XT(Xw^−y)=0得w^=(XTX)−1XTy至此,便解出了多元线性回归模型。
二、对数几率回归
(一)广义线性模型
线性模型虽简单,却有丰富的变化,线性回归模型可简写为 y = w T x + b y=w^Tx+b y=wTx+b,假设某一情况中对应的输出是在指数尺度上变化,那就可将输出的对数作为线性模型逼近的目标,即: l n y = w T x + b lny=w^Tx+b lny=wTx+b上式在形式上仍是线性回归,但实质上已是在求取输入空间到输出空间的非线性函数映射。这里的对数函数起到了将线性回归模型的预测值与真实的标记联系起来的作用。
更一般地,考虑单调可微函数 g ( ⋅ ) g(\cdot) g(⋅),令 y = g − 1 ( w T x + b ) y=g^{-1}(w^Tx+b) y=g−1(wTx+b)这样得到的模型称为“广义线性模型”(generalized linear model),其中函数 g ( ⋅ ) g(\cdot) g(⋅)称为“联系函数”(link function)。
(二)对数几率回归公式推导
1. 对数几率回归模型
上一节讨论了如何使用线性回归模型进行学习,但若要做的是分类任务该怎么办?答案蕴含在广义线性模型中:只需找到一个单调可微函数将分类任务的真实标记与线性回归模型的预测值联系起来。
考虑二分类任务,其输出标记 y ∈ { 0 , 1 } y\in\{0,1\} y∈{0,1},而线性回归模型产生的预测值 y = ( w T x + b ) y=(w^Tx+b) y=(wTx+b)是实值,于是需要找到一个函数将实值转化为0/1值,对数几率函数就是这样一个合适的函数。对数几率函数如图所示: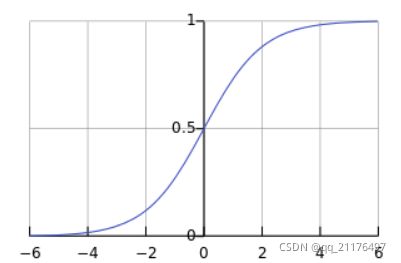
其表达式为: y = 1 1 + e − z y={1\over {1+e^{-z}}} y=1+e−z1,将其作为 g − ( ⋅ ) g^-(\cdot) g−(⋅)带入 y = g − 1 ( w T x + b ) y=g^{-1}(w^Tx+b) y=g−1(wTx+b),即可得对数几率回归模型: y = 1 1 + e − ( w T x + b ) = e w T x + b 1 + e w T x + b y={1\over{1+e^{-(w^Tx+b)}}}={e^{w^Tx+b}\over1+e^{w^Tx+b}} y=1+e−(wTx+b)1=1+ewTx+bewTx+b
2. 极大似然估计方法
哪一组参数使得现在的样本观测值出现的概率最大,哪一组参数可能就是真正的参数,我们就用它作为参数的估计值,这就是所谓的极大似然估计。已知随机变量的 y y y取1和0的概率分别为
p ( y = 1 ∣ x ) = e w T x + b 1 + e w T x + b p ( y = 0 ∣ x ) = 1 1 + e w T x + b p(y=1|x)={e^{w^Tx+b}\over1+e^{w^Tx+b}}\\p(y=0|x)={1\over1+e^{w^Tx+b}} p(y=1∣x)=1+ewTx+bewTx+bp(y=0∣x)=1+ewTx+b1 令 β = ( w ; b ) , x ^ = ( x , 1 ) \beta=(w;b),\hat x=(x,1) β=(w;b),x^=(x,1),则 w T x + b w^Tx+b wTx+b可简写为 β T x ^ \beta^T\hat x βTx^,于是上式可简化为 p ( y = 1 ∣ x ) = e β T x ^ 1 + e β T x ^ = p 1 ( x ^ ; β ) p ( y = 0 ∣ x ) = 1 1 + e β T x ^ = p 0 ( x ^ ; β ) p(y=1|x)={e^{\beta^T\hat x}\over1+e^{\beta^T\hat x}}=p_1(\hat x;\beta)\\p(y=0|x)={1\over1+e^{\beta^T\hat x}}=p_0(\hat x;\beta) p(y=1∣x)=1+eβTx^eβTx^=p1(x^;β)p(y=0∣x)=1+eβTx^1=p0(x^;β)可得:
p ( y ∣ x ; w , b ) = y ⋅ p 1 ( x ^ ; β ) + ( 1 − y ) ⋅ p 0 ( x ^ ; β ) p(y|x;w,b)=y\cdot p_1(\hat x;\beta)+(1-y)\cdot p_0(\hat x;\beta) p(y∣x;w,b)=y⋅p1(x^;β)+(1−y)⋅p0(x^;β)或者:
p ( y ∣ x ; w , b ) = [ p 1 ( x ^ ; β ) ] y [ p 0 ( x ^ ; β ) ] 1 − y p(y|x;w,b)=[p_1(\hat x;\beta)]^y[p_0(\hat x;\beta)]^{1-y} p(y∣x;w,b)=[p1(x^;β)]y[p0(x^;β)]1−y在许多情况下,求解似然函数的对数 l n L ( w ) lnL(w) lnL(w)比求解似然函数本身 L ( w ) L(w) L(w)更简单,通常称 l n L ( w ) lnL(w) lnL(w)为对数似然函数。 l ( w , b ) = ∑ i = 1 m l n p ( y i ∣ x i ; w , b ) l(w,b)=\sum_{i=1}^mlnp(y_i|x_i;w,b) l(w,b)=i=1∑mlnp(yi∣xi;w,b)将概率值带入对数似然函数,最大化似然函数,等价于最小化:
l ( β ) = ∑ r = 1 m ( − y i β T x ^ i + l n ( 1 + e β T x ^ i ) ) \begin{aligned} l(\beta)&=\sum_{r=1}^m(-y_i\beta^T\hat x_i+ln(1+e^{\beta^T\hat x_i}))\end{aligned} l(β)=r=1∑m(−yiβTx^i+ln(1+eβTx^i))便可求出参数的估计: β ∗ = a r g min β l ( β ) \begin{aligned}\beta^*&=arg\,\min_{\beta}l(\beta) \end{aligned} β∗=argβminl(β)