股价/期货等时间序列数据的整合检验、Grach建模

股价/期货等时间序列数据的整合检验、Grach建模

前言

之前解决一个金融方向的时间序列类问题的实验，因为要形成一个完整的论文，自己从头开始学的时候，把需要的实验和作图整合了一下。其中包括了时间序列数据的简单收益率、对数收益率的计算。数据的稳定性检验(单位根检验、自相关检验、偏相关检验)、白噪声检验、JB检验。还有QQ、PP图、频率分布图等作图。
最后还有GRACH建模。应该能从头到尾解决一个时间序列数据的从检验到建模的论文撰写，希望能方便大家。

如果对大家有帮助，希望可以点个star。
github地址：https://github.com/bamboosir920/Time-series-data-complete-experimental-integration-package
gitee地址：https://gitee.com/bamboosir920/Time-series-data-complete-experimental-integration-package

示例

数据格式：

示例：

代码

main.py

#格式 日期 价格(元/吨)
import numpy as np
import csv
from TStest import *
from TSbase import *


sns.set()  #切换到sns的默认运行配置
#避免中文显示不出来
matplotlib.rc("font",family='KaiTi')
#避免负号显示不出来
matplotlib.rcParams['axes.unicode_minus']=False
#导入数据
p=r'./xxx.csv'
with open(p) as f:
    data=np.loadtxt(f,str,delimiter=',') 
x=np.array(data[:,0])
y=np.array(data[:,1])
y = y.astype(np.float64)



'''
基础作图
'''
baseimg(data=y,date=x,xlabel="时间",ylabel="收盘价",x_loc=500,y_loc=500)

'''
收益率
'''
# 简单收益率
simpleReturn=simple_return_rate(y,False)
# 对数收益率
logReturn=log_return_rate(y,False)

'''
JB检验
'''
print(JBtest(logReturn))

'''
平稳性检验
'''
TS_ADF(logReturn)
TS_ACF(logReturn)
TS_PACF(logReturn)

'''
大图
# '''
ts_plot(logReturn,lags=30,title='对数收益率')

'''
白噪声检验
'''
white_test(simpleReturn,12)
white_test(logReturn,30)

'''
频率分布图
'''
frequency_distribution(logReturn,title='频率分布图')

'''
Garch建模
'''
Arch(logReturn)

'''
预测
'''
predict(y,logReturn,20000,'..')

TSbase.py

import numpy as np
import matplotlib
import matplotlib.pyplot as plt
#从pyplot导入MultipleLocator类,这个类用于设置刻度间隔
from matplotlib.pyplot import MultipleLocator
from math import *
#避免中文显示不出来
matplotlib.rc("font",family='KaiTi')
#避免负号显示不出来
matplotlib.rcParams['axes.unicode_minus']=False
#tsa为Time Series analysis缩写
import statsmodels.api as sm
import scipy.stats as scs
import seaborn as sns
# 导入 arch 包中的 arch_model 模块
from arch import arch_model

'''
用来绘制基础随时间而变化趋势图

date:时间,x轴
data:数据,y轴,具体数值
title:标题
xlabel:横坐标注释
ylabel:纵坐标注释
x_loc:X轴默认刻度,默认值为10
y_loc:y轴默认刻度,默认值为10
colors:折线颜色,默认为'#0066cc'
'''
def baseimg(data,date,title='',xlabel='',ylabel='',x_loc=10,y_loc=10,colors='#0066cc'):
    #绘制网格
    plt.grid(alpha=0.6,linestyle=':')
    #作图
    plt.plot(date,data,color=colors)
    #把x轴的刻度间隔设置为500,并存在变量里
    x_major_locator=MultipleLocator(x_loc)
    #把y轴的刻度间隔设置为500,并存在变量里
    y_major_locator=MultipleLocator(y_loc)
    #ax为两条坐标轴的实例
    ax=plt.gca()
    #把x轴的主刻度设置为500的倍数
    ax.xaxis.set_major_locator(x_major_locator)
    #把y轴的主刻度设置为500的倍数
    ax.yaxis.set_major_locator(y_major_locator)
    #设置标题、x轴注释、y轴注释
    plt.title(title,fontsize=16)
    plt.xlabel(ylabel,fontsize=12)
    plt.ylabel(xlabel)
    plt.show()
    return 0

'''
Logarithmic return rate
对数收益率
对数收益率: 所有价格取对数后两两之间的差值。

input:
data:数据
is_img:是否作图,True/False
title:标题名
colors:折线颜色,默认为'#0066cc'
'''
def log_return_rate(data,is_img=True,title='Logarithmic return rate',colors='#0066cc'):
    logReturn = np.diff(np.log(data))
    if is_img==True:
        plt.plot(logReturn,color=colors)
        plt.title(title,fontsize=16)
        plt.show()
    return logReturn

'''
simple return of rate
简单收益率
input:
data:数据
is_img:是否作图,True/False
title:标题名
colors:折线颜色,默认为'#0066cc'
'''
def simple_return_rate(data,is_img=True,title='simple return of rate',colors='#0066cc'):
    simpleReturn = np.diff(data)
    if is_img==True:
        plt.plot(simpleReturn,color=colors)
        plt.title(title,fontsize=16)
        plt.show()
    return simpleReturn

'''
价格预测
input:
data:价格序列
ret:收益率
count:拟合次数
title:标题
'''
def predict(data,ret,count,title=''):
    # 设置一个空列表来保存我们每个模拟价格序列的最终值
    result = []

    S = data[-1] #起始股票价格（即最后可用的实际股票价格）
    T = 252 #交易天数
    all=0

    mu=np.mean(ret) #收益率
    vol=np.std(ret)*sqrt(252/len(data)) #波动率


    #选择要模拟的运行次数-我选择了10,000
    for i in range(count):
    #使用随机正态分布创建每日收益表
        daily_returns=np.random.normal((1+mu)**(1/T),vol/sqrt(T),T)
        #设定起始价格，并创建由上述随机每日收益生成的价格序列
    price_list = [S]
    for x in daily_returns:
        price_list.append(price_list[-1]*x)
        #将每次模拟运行的结束值添加到我们在开始时创建的空列表中
        result.append(price_list[-1])

    plt.figure(figsize=(10,6))
    plt.hist(result,bins= 100)
    plt.axvline(np.percentile(result,5), color='r', linestyle='dashed', linewidth=2)
    plt.axvline(np.percentile(result,95), color='r', linestyle='dashed', linewidth=2)
    mean=np.mean(result)
    a5=result[int(len(result)/5)]
    a95=result[-int(len(result)/5)]
    print(mean)
    print(a95)
    print(a5)
    plt.figtext(0.8,0.8,s="起始价格: %.2f元" %S)
    plt.figtext(0.8,0.7,"平均价格 %.2f 元" %mean)
    plt.figtext(0.8,0.6,"5%"+" 置信度: %.2f元" %a5)
    plt.figtext(0.15,0.6, "95%" +"置信度: %.2f元" %a95)
    plt.title(title, weight='bold', fontsize=12)
    plt.show()
    

'''
频率分布图
Histogram of frequency distribution
input:
data:数据
title:标题
'''
def frequency_distribution(data,title='频率分布图'):
    sns.distplot(data, color='blue') #密度图
    plt.title(title,fontsize=16)
    plt.show()
    
'''
grach建模
input:
data:数据
title1:拟合ARCH残差图标题
title2:条件方差图标题
vol (str, optional) 波动率模型的名称，目前支持: 'GARCH' （默认）, 'ARCH', 'EGARCH', 'FIARCH' 以及 'HARCH'。
p (int, optional) 对称随机数的滞后阶（译者注：即扣除均值后的部分）。
o (int, optional)  非对称数据的滞后阶
q (int, optional)  波动率或对应变量的滞后阶
power (float, optional)  使用GARCH或相关模型的精度
dist (int, optional) 误差分布的名称，目前支持下列分布：
    正态分布: 'normal', 'gaussian' (default)
    学生T分布: 't', 'studentst'
    偏态学生T分布: 'skewstudent', 'skewt'
    通用误差分布: 'ged', 'generalized error”
'''
def Arch(data,p_=2,q_=2,o_=1,power_=2.0,vol_='Garch',dist_='StudentsT',title1='对比图',title2='拟合残差',title3='条件方差'):
     # 设定模型
    am=arch_model(data, p=p_, q=q_, o=o_,power=power_, vol=vol_, dist=dist_)
    res = am.fit(update_freq=5, disp='off')
    print(res.summary())

    fig = res.hedgehog_plot(type='mean')
    plt.title(title1,size=15)
    plt.show()

    plt.plot(res.resid)
    plt.title(title2,size=15)
    plt.show()
    
    plt.plot(res.conditional_volatility,color='r')
    plt.title(title3,size=15)
    plt.show()

TStest.py

import pandas as pd
import statsmodels.tsa.api as smt     
#tsa为Time Series analysis缩写
import statsmodels.api as sm
import scipy.stats as scs
from arch import arch_model
import numpy as np
import matplotlib
import matplotlib.pyplot as plt

from statsmodels.stats.diagnostic import acorr_ljungbox

#从pyplot导入MultipleLocator类,这个类用于设置刻度间隔
from matplotlib.pyplot import MultipleLocator
#引入单位根检验
from arch.unitroot import ADF
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf

import numpy as np
import scipy.stats as stats
#避免中文显示不出来
matplotlib.rc("font",family='KaiTi')
#避免负号显示不出来
matplotlib.rcParams['axes.unicode_minus']=False


'''
做一个完整检验的大图

input:
data:输入y轴数值
lags:延迟
title:标题

'''
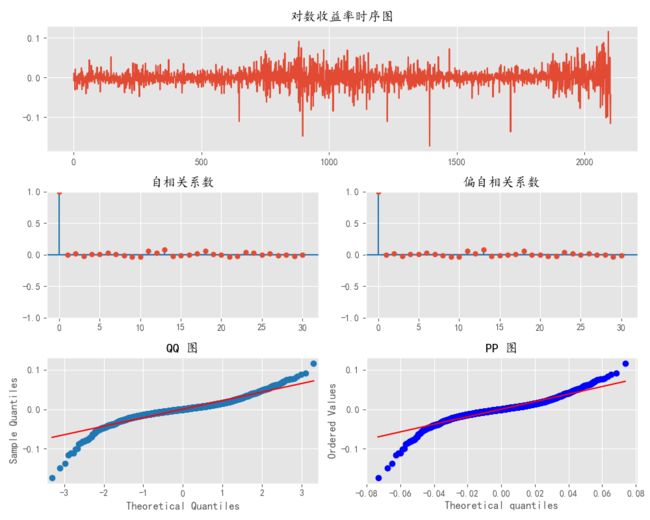
def ts_plot(data, lags=None,title=''):    
    if not isinstance(data, pd.Series):           
        data = pd.Series(data)    
        #matplotlib官方提供了五种不同的图形风格，    
        # #包括bmh、ggplot、dark_background、    
        # #fivethirtyeight和grayscale    
        with plt.style.context('ggplot'):            
            fig = plt.figure(figsize=(10, 8))        
            layout = (3, 2)        
            ts_ax = plt.subplot2grid(layout, (0,0),colspan=2)        
            acf_ax = plt.subplot2grid(layout, (1, 0))        
            pacf_ax = plt.subplot2grid(layout, (1, 1))        
            qq_ax = plt.subplot2grid(layout, (2, 0))        
            pp_ax = plt.subplot2grid(layout, (2, 1))        
            data.plot(ax=ts_ax)        
            ts_ax.set_title(title+'时序图')        
            smt.graphics.plot_acf(data, lags=lags,ax=acf_ax, alpha=0.5)        
            acf_ax.set_title('自相关系数')        
            smt.graphics.plot_pacf(data, lags=lags,ax=pacf_ax, alpha=0.5)        
            pacf_ax.set_title('偏自相关系数')        
            sm.qqplot(data, line='s', ax=qq_ax)        
            qq_ax.set_title('QQ 图')                
            scs.probplot(data, sparams=(data.mean(),data.std()), plot=pp_ax)        
            pp_ax.set_title('PP 图')         
            plt.tight_layout()
            plt.show()    
            return

'''
时间序列稳定性检验,单位根ADF

input:
data:输入y轴数值
name:数值含义

output:
Test Statistic : T值,表示T统计量
p-value: p值,表示T统计量对应的概率值
Lags Used:表示延迟
Number of Observations Used: 表示测试的次数
Critical Value 1% : 表示t值下小于 - 4.938690 , 则原假设发生的概率小于1%, 其它的数值以此类推。

其中t值和p值是最重要的,其实这两个值是等效的,既可以看t值也可以看p值。
p值越小越好,要求小于给定的显著水平,p值小于0.05,等于0最好。
t值,ADF值要小于t值,1%, 5%, 10% 的三个level,都是一个临界值,如果小于这个临界值,说明拒绝原假设。
1%、%5、%10不同程度拒绝原假设的统计值和ADF Test result的比较,ADF Test result同时小于1%、5%、10%即说明非常好地拒绝该假设.
P-value是否非常接近0.
'''
def TS_ADF(data):
    print("**************************************************************************")
    print("**************************************************************************")
    print("Time Series test————ADF")
    res=np.array(ADF(data))
    print(res)
    print("*************************************************************************")
    print("*************************************************************************")
    return res

'''
时间序列稳定性检验,自相关检验ACF

input:
data:输入数据

结果含义:
ACF 是一个完整的自相关函数,可为我们提供具有滞后值的任何序列的自相关值。
简单来说,它描述了该序列的当前值与其过去的值之间的相关程度。
时间序列可以包含趋势,季节性,周期性和残差等成分。
ACF在寻找相关性时会考虑所有这些成分。
直观上来说,ACF 描述了一个观测值和另一个观测值之间的自相关,包括直接和间接的相关性信息。

截尾:在大于某个常数k后快速趋于0为k阶截尾
拖尾:始终有非零取值,不会在k大于某个常数后就恒等于零(或在0附近随机波动)
'''
def TS_ACF(data):
    plot_acf(data)
    plt.show()

'''
时间序列稳定性检验,偏自相关函数PACF

input:
data:输入数据

结果含义:
PACF 是部分自相关函数或者偏自相关函数。
基本上,它不是找到像ACF这样的滞后与当前的相关性,而是找到残差（在去除了之前的滞后已经解释的影响之后仍然存在）与下一个滞后值的相关性。
因此,如果残差中有任何可以由下一个滞后建模的隐藏信息,我们可能会获得良好的相关性,并且在建模时我们会将下一个滞后作为特征。
请记住,在建模时,我们不想保留太多相互关联的特征,因为这会产生多重共线性问题。因此,我们只需要保留相关功能。

截尾:在大于某个常数k后快速趋于0为k阶截尾
拖尾:始终有非零取值,不会在k大于某个常数后就恒等于零(或在0附近随机波动)
'''
def TS_PACF(data): 
    plot_pacf(data)
    plt.show()

'''
白噪声检验
'''
def white_test(data,lag=25):
    print(acorr_ljungbox(data, lags = lag,boxpierce=True))
    return acorr_ljungbox(data, lags = lag,boxpierce=True)

'''
JB检验：
input:
data:输入数据、序列

output：
偏度、峰值、JB检验
'''

def JBtest(data):
    # 样本规模n
    n = data.size
    data_ = data - data.mean()
    """
    M2:二阶中心钜
    skew 偏度 = 三阶中心矩 与 M2^1.5的比
    krut 峰值 = 四阶中心钜 与 M2^2 的比
    """
    M2 = np.mean(data_**2)
    skew =  np.mean(data_**3)/M2**1.5
    krut = np.mean(data_**4)/M2**2

    """
    计算JB统计量，以及建立假设检验
    """
    JB = n*(skew**2/6 + (krut-3 )**2/24)
    pvalue = 1 - stats.chi2.cdf(JB,df=2)
    print("偏度：",stats.skew(data),skew)
    print("峰值：",stats.kurtosis(data)+3,krut)
    print("JB检验：",stats.jarque_bera(data))
    return np.array([JB,pvalue])