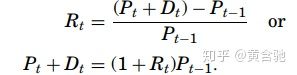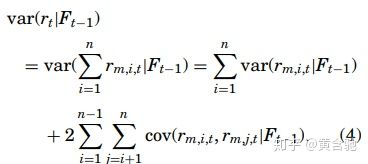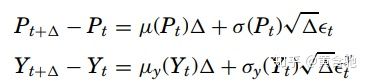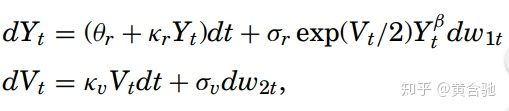一阶差分序列garch建模_量化小白暑期研究笔记(8)——金融时间序列综述论文解读...

论文:

`Financial Time Series''. In: Encyclopedia of Statistical Sciences​onlinelibrary.wiley.com

-----------------------------------------------------------------------------读前须知:

Excess kurtosisis :

a statistical term describing that a probability, or return distribution, has a kurtosis coefficient that is larger than the coefficient associated with a normal distribution, which is around 3---------------------------------------------------------------------------------------------

涉及模型及统计方法:

GARCH（p,q） Box-Ljung统计 BS公式 吉布斯迭代

----------------------------------------------------------------------------------------------

ASSET PRICE AND RETURN

Pt: t时刻资产价格 Fh: h时刻可获得的公开信息 Dt: (t − 1,t]时间所获股利
给定Fh, 金融时间序列和Pt&Dt随时间的演化有关

实际操作中经常使用2种return,

第一种simple return Rt定义为

第二种continuously compounded return or log return定义为

这两种return的关系是rt = ln（1 + Rt），每种return在应用中都有自己的优点。 例如，一个多期对数收益只是一定时间间隔中单周期对数收益的时间聚合，而投资组合的简单收益是各个简单收益的加权平均值，每个资产的权重是投资组合在该资产中价值的百分比。

金融业的另一个重要概念是风险。 还不错的金融投资应收获超过无风险利率的收益。 因此，一些财务研究使用风险调整后的收益。 资产的超额收益是资产收益率与某些无风险参考资产收益率间的差额，例如短期美国国库券收益。 我们在本文中使用了对数收益，但讨论的思路和方法适用于其他收益。

表1（a）给出了所选美国股票和标准普尔500指数每日对数收益率的百分比汇总统计数据。该表清楚地显示了每日股票收益的一些特殊特征。首先，每日对数收益的样本均值很小，但样本方差很大。其次，存在一些（消极的）偏斜。第三，返回序列具有高过度峰度(high excess kurtosis)。第四，如果存在序列相关性，那它对于每日股票收益来说是微弱的。表1（b）显示了所选汇率月度对数收益的相同统计数据。观察到类似的特征，但汇率序列具有显着的1阶滞后序列相关性。

图1显示了标准普尔500指数的每日对数收益时间图。该图显示了阶段性的高低变动(periods of high and low variabilities)。 这种现象被称为金融中的波动性聚集( volatility clustering)。 图2显示了标准普尔500指数的对数收益和对数收益绝对序列的样本自相关函数（ACF）。对数收益的ACF很小，但绝对序列的ACF很大并且衰减缓慢。因此，对数收益基本上连续不相关(serially uncorrelated)，但高度依赖。基于该序列的经验特征，给定Fh且t> h时,rt的精确条件分布在实践中难以指定。 因此，大部分研究都集中在给定Fh时rt前两个条件矩的时间演化上。

金融时间序列分析的目的是研究μt和σt之间的性质和关系。σt通常被称为序列波动性,它是金融风险的衡量标准，在衍生品定价中发挥着重要作用。 σt随时间变化的fact被称为条件异方差性。

FUNDAMENTAL AND TECHNICAL ANALYSES

将金融时间序列分析与其他统计分析区分开来的一个关键特征是重要的波动率变量σt不能直接观察到。 因此，有学者设计了特殊的模型和方法来分析金融时间序列，且分析可分为两种一般性的方法。

第一种方法研究μt与其他经济和市场变量之间的关系，如利率，国内生产总值增长率，通货膨胀率，消费者信心指数，失业率，贸易不平衡，企业收益，账面市场比率等。这被称为基本分析，它通常采用具有时间序列误差的回归模型，包括条件异方差性和因子分析。 用xt表示解释变量的向量，它的第一个元素是1。 回归模型如下:

未知参数β常用最小二乘估计,但必须进行调整以考虑方差估计中的异方差性。(???)

当xt的维数很大时，使用因子和主成分分析等降维方法来简化模型。

第二种方法探讨了给定Ft-1时rt的动态依赖性，并被称为技术分析。时间序列方法和随机过程是这种方法使用的主要工具。假设μt和σ^2t的依赖结构都满足动态线性模型。由于rt中的连续相关性serial correlation较弱，如表1和图2（a）所示，μt的动态结构相对简单,它通常是常数或Ft-1元素的简单函数(eg:一个简单的自回归模型). 相反，σ^2t的动态依赖性更复杂。特别是众所周知的是{r^2t}和{| rt |}序列有很强的序列相关性。见图2（b）。再举一个例子，考虑表1中美铝库存的每日对数收益。{r2t}和{| rt |}的Box-Ljung统计分别给出Q（10）= 574和Q（10）= 519。在{rt}是独立同分布（iid）随机变量的假设下，这些统计数据与其具有10个自由度的渐近卡方分布相比非常具有显着性。对序列{σ^2t}进行建模被称为波动率建模。为了便于讨论，我们将对数收益重写为

在实践中，epsilon_t通常被假定为标准正态分布或具有v自由度的标准化Student-t分布或广义误差分布。 在许多应用中，基本分析和技术分析需结合使用.

VOLATILITY MODEL GARCH

Family of Models

波动率建模有三种方法。 第一种指定了σ^2_t的固定函数，称为广义自回归条件异方差（GARCH）建模。σ^2_t的GARCH（p，q）模型定义为

for i≠j

因此,{ηt}是一不相关的序列。 但是，它们并不同分布。 我们可以重写GARCH为:

它是{(a_t)^2}序列的自回归移动平均（ARMA）模型的形式，其中如果i> p，则αi= 0，如果i> q，则βi= 0。 GARCH模型的许多性质可以从ARMA模型中推导出来。其中两个性质在金融时间序列分析中特别相关。首先,对一个给定模型,

或

中的大元素生成了一个大的

这反过来暗示将会有更大概率得到一个令人吃惊的a_t.故而GARCH模型能描述之前提到的波动率聚类。 其次，该模型可能具有高过度峰度 high excess kurtosis。 实际上，GARCH(p，q)模型中a_t的过度峰度excess kurtosis表达式如下(???)

(the fourth ...没懂)

GARCH的一个主要弱点是他们假设模型在波动率(σ_t)^2上的正负冲击a_(t-i)是对称的. (见下图,没懂)

另一方面，经验证据表明，大的正负面冲击对资产收益影响相当不同。为克服这个缺点，学界已研究出GARCH模型的许多变体，如指数GARCH模型.

条件最大似然法常被用于GARCH估计。

若epsilon_t不是高斯型,方程2的L(theta)也常常被最小化(原文就是写的最小化,可这里不是明显该最大化么)来获得theta的准最大似然估计QMLE.用theta_o来表示真实参数，l= 1 + p + q表示GARCH（p，q）参数个数。将(σ_t)^2重写成过去误差项past error terms的函数(误差项如下)

(接下来2张图没看懂)

这个定理和金融时间序列分析特别相关，因为金融时间序列往往重尾现象。Hall和Yao [14]建议使用Bootstrap方法来获得theta hat的临界值.

Stochastic Volatility Model

波动率建模的另一种方法是假设潜在波动率的随机模型。 通常使用简单的自回归来生成模型

额外的创新---{ηt}大大增加了随机波动率（SV）模型在模拟不断变化市场条件时的灵活性。 然而，这种优势伴随着估计复杂性的代价。

对于大或中等样本大小n，评估该似然函数的有效方法是将Hn视为增强数据并应用蒙特卡罗方法，例如采用吉布斯采样的马尔可夫链蒙特卡罗（MCMC）方法。

Realized Volatility

高频金融数据的出现，例如 股票市场的交易数据使得日内收益的二次变化成为波动率建模的可行替代方案。 这种方法的基本思想已存在多年。 例如，在[12]中使用每日对数收益来估计每月对数收益的波动性。 考虑估计对数收益序列的每日波动率问题。 使用log return的附加属性，每日收益是日内收益的时间聚合，即

r_t的方差为

在一些一般性条件下，方程4波动性可直接根据日内对数收益估算。 例如，如果

序列不相关,那么

是对每日波动率平方的一致估计。 这种估计在文献[2]中称为现实波动率。如若r_{m,i,t}是1阶滞后序列相关的(如:服从一阶滑动平均模型,那么

是对每日波动率平方的一致估计。 对于日内指数收益，如标普500，1阶滞后序列相关似乎很重要，特别在时间间隔很短时。 对于汇率和个股序列，日内对数收益的序列相关性相对较小。 现实波动率作为波动率估计的有效性在很大程度上取决于日内对数收益的过度峰度; 过度峰度越高，估计效率越低。

经验表明，实现波动率的对数边际分布近似正常。对数波动率序列也表现出长程依赖性的特征，例如，对数波动率序列的样本自相关性随着滞后的增加而缓慢衰减。线性时间序列模型（包括分数差异模型）已用于拟合{ln（σ2t）}序列，拟合模型用于生成波动率预测。

Remark 1.我们基于资产收益率对波动率进行了讨论。在期权市场中，交易期权的观察价格可借助著名的Black Scholes公式推导出相应的波动率。然而，隐含波动率取决于所使用的具体期权。 在实践中经常使用价内的短期看涨期权。(why?)

插图例证

图3（a）显示了标准普尔500指数从1926年到2001年912次观测的每月对数收益（百分比）。 该序列已在文献中被广泛研究. 如果高斯GARCH模型are entertained(不理解)，我们得到

其中括号中的数字表示渐近标准误差。令e_t=(r_t − 0.695)/(σ_t hat)为标准化残差.{et}和{e2t}的Box-Ljung统计给出Q（10）= 11.68（0.31）和Q（10）= 5.44（0.86），其中括号中的数字表示p值。因此，简单的GARCH（1,1）模型足以描述标准普尔500指数月度收益的前两个条件矩。 然而，标准化残差{et}的偏度和过度峰度分别为-0.717和2.057，表明e_t不是正态分布的。 图3（b）显示了年化波动率(GARCH（1,1）模型的σt×√12)序列.

方程5中的GARCH（1,1）模型具有实践中常见GARCH模型的几个特征。首先，α1+β1= 0.9811，接近但小于1，表示波动性高度抗性。它还表明，波动可能存在跳跃。

因此，对数返回具有高过量峰度。 实际上，拟合的GARCH（1,1）模型给出了7.58的过度峰度，这非常接近数据的过度峰度7.91;

对于随机波动率建模，我们将带有吉布斯采样的MCMC方法应用于数据; 有关详细信息，请参见[19]的第10章。 使用4000次迭代(其中前1000次迭代作为老化测试)，我们获得模型

其中系数是最后3000次吉布斯迭代的后验平均值，括号中的数字是后验标准误差。 图3（c）显示了数据的年化波动率，即后验均值。 该图显示了与GARCH（1,1）模型类似的模式，但20世纪80年代的波动率峰值似乎比GARCH（1,1）模型的波动率更高。 AR（1）中较大的系数也支持波动性的持续性.

可以以与ARMA模型相同的方式获得GARCH模型的预测。 这里估计的参数通常被视为已给定。 另一方面，若我们使用模拟技术来生成SV模型的预测,预测结果可接受参数不确定性，不过这需要进行密集计算.

HIGH-FREQUENCY DATA

逐笔交易市场数据的可用性为市场微观结构的实证研究开辟了一条新途径。例如，论文[5]使用在台湾证券交易所交易的345只股票的盘中5分钟收益，以建立由每日价格限制引起的统计和经济上显着的磁铁效应magnet effects 。通过磁铁效应，价格在接近极限时会加速到极限。高频数据具有许多在低频下观察数据时不会发生的特性。首先，交易不以相等时间间隔发生.其次，交易强度因交易时间而异;通常在交易日市场开盘和收盘时会出现更高的强度。第三，交易价格假定为离散值。第四，每笔交易产生若干变量，包括交易时间，买入价和卖出价，交易价格，交易量，depths of bid and ask等。第五，样本量大。如在1999年12月的正常交易期间，IBM股票的交易量超过133,000笔。（第三四点估计低频也可以吧？）

现在，以上特性已成为高频数据统计分析的新挑战。众所周知，非同步交易可能导致投资组合及个股收益中的负序列相关性negative serial correlations 。买卖价差在数据频率高时也会引入股票价格变化的1阶强负滞后序列相关性。因此，观察到的资产收益中存在序列相关性并不一定与金融中的有效市场假设相矛盾。

这些特征也为统计学家提供了新的研究机会。例如，第二个特征导致日内序列明显的昼夜模式，即每日季节性。如何有效地模拟昼夜模式及模式对数据统计特性有何影响，这些问题都有待进一步挖掘。再例如，连续交易间的时间间隔不仅在分析不等间隔时间序列时很有必要，在新事件发生时也能提供很有价值的信息;当有新信息传播时，交易往往更重。考虑交易区间中嵌入的信息内容会导致新式统计模型的发展，如[10]中的条件自回归持续时间模型。有关高频金融数据的进一步讨论，请参见[19]中的[6]和第5章。一般而言，当观察频率(observational frequency(??))较高时，证券市场制度安排对金融时间序列的影响变得更加明显。必须正确处理这种制度效应，以便对所研究的系列作出合理的推断。

CONTINUOUS-TIME MODEL

金融时间序列的应用必须基于离散时间观测。然而，资产定价的大部分理论都是基于连续时间模型。 金融工程文献中一个活跃的研究领域是使用离散观察的时间序列数据来估计连续时间模型。 资产价格Pt的简单扩散方程是

wt 是一个standard Brownian motion (或Wiener process)。µ(Pt) 与 σ(Pt)都是满足某些规律性条件的光滑函数，因此Pt通过随机积分存在。 例如，欧洲期权的Black-Scholes定价公式就基于几何布朗运动，dPt =μPtdt+σPtdwt，其中μ和σ是常数。 在此简单情况下，可应用Ito的引理来获得资产从时间t到t +的对数收益分布。 分布是高斯分布

r bar 和 s^2分别是收益的样本均值与方差。

在很多应用中，函数µ(Pt) 与 σ(Pt)未知，并且无法得到Pt的closed-form solution。另外，为更好地描述隐含波动率的经验特征，如波动率微笑，σ（Pt）被扩展为由另一个维纳过程驱动的随机波动。 微笑效应表示期权价格的隐含波动率在期权范围内不是常数，它随执行价格和期权到期时间变化而变化。

结合两个扩散方程，我们得到一个具有随机波动率的一般连续时间模型

方程6、7中基于离散观测数据的扩散方程估计是衍生品定价中的重要问题。 在一定时间间隔中，模型的离散时间近似是

其中

是双变量正态随机变量，均值为零，方差为1，相关系数为ρ。扩散方程的这种天真离散化可能导致参数估计中的离散化偏差(尤其当Delta很大时)。已有学者设想了不错的统计方法将两个连续观察之间的过程值视为缺失值以减少近似偏差。这通常通过[11]和[8]中的MCMC方法完成。另一方面，如果Delta太小，则市场微观结构对P{t + Delta}- P_{t}的影响变得明显。这需要我们在市场微观结构引起的近似精度和观测噪声之间进行权衡。其他估算扩散方程的方法包括[13]中矩的有效方法，[1]中的非参数方法，以及[15]中矩的广义方法等。最后，随机跳跃可添加到6式、7式的扩散方程中，以更好地描述隐含波动率的经验特征。

插图例证

图4显示了从1/1/1954到10/5/1997对每周三美国国库券收益率的2288次观察。该系列在[11]中用于说明扩散方程的估计。 我们使用相同数据和我们自己的程序来重现结果。表2（a）给出了数据的描述性统计，它与[11]中数据能很好地匹配。 首先，考虑如下形式中的简单恒定方差弹性（CEV）模型

Y_t:利率

除β外，参数的条件后验分布都是标准的，可在MCMC迭代中轻松绘制。β则可用混合接受/拒绝Metropolis-Hasting算法来绘制。 表2（b）给出了基于20,000吉布斯迭代的估计结果。 令人欣慰的是，两项独立估计的结果非常一致。 接下来，考虑随机波动率（SV）模型，形式如下

简单来说，w1t和w2t是两个独立的标准布朗运动。 这里计算强度显着增加，因为波动率序列是一个潜在过程。表2（c）显示了美国利率序列的SV模型的结果。 利率用百分比格式表示。 利率扩散方程的估计与CEV模型的估计类似，但它们与Eraker（2001）的估计存在一些差异。