基于神经网络进行数据降维

前言

机器学习方法降维可以说非常多了，无论是线性还是非线性，而且各有各的优势存在。本篇文章主要是基于神经网络的自编码技术对数据进行降维，无论是一维特征构成的样本数据（只有长或者宽有数据）还是3维特征构成的数据（图像数据长、宽、高）等都可以通过自编码器进行数据降维。

一：自编码器介绍

• 我们简单介绍下什么叫自编码器

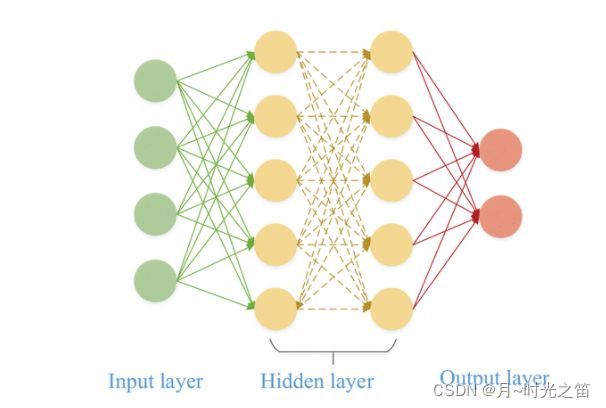
自编码器（autoencoder, AE）是一类在半监督学习和非监督学习中使用的人工神经网络其功能是通过将输入信息作为学习目标，对输入信息进行表征学习，其输出维度一般远小于输入维度，所以一般用于降维分析。自编码器包含编码器（encoder）和解码器（decoder）。

图1

从上图1中，我们把输入的高维数据到输入隐藏层，称为编码过程，通过学习到的权重信息，我们将得到隐藏层到Bottleneck层的数据，也就是我们的目标降维数据，再把降维数据映射到输出隐藏层，最终输出隐藏层的数据尽可能还原成原本数据，称为解码过程，那么还原回来的数据也可称为重构数据，重构数据与原始数据的误差称为重构误差，我们的目标就是使重构误差尽可能的小，基于此来不停的学习和更新隐藏层数据和Bottleneck层数据。这就是自编码器的一般原理（我们从图一的数据维度的变化能更直观感受这一降维和还原过程）。

此结构降维的数据本质上跟传统的PCA是一样的，最终降维数据都是通过矩阵运算组合得到的，但它又比一般PCA性能强大，毕竟它是基于非线性计算规则而且还是基于网络自主监督学习更新。

• 噪声或异常值存在情况

1：如果我们的目标是降维，那么噪声的存在必定会对降维的数据造成干扰，所以去噪声是务必要进行的，

2：如果我们的目标是检测噪声或者异常值的存在，那么先前的所有样本通过自编码器各个还原后，计算重构误差（可选MSE），如果MSE的值明显出现很大或者很异于正常样本值，那么可以判断此样本存在异常值，

3：当然，异常值或者噪声的存在不能过多，否则很容易产生过拟合现象。

• 其他自编码器

收缩自编码器（contractive autoencoder）

正则自编码器（regularized autoencoder）

变分自编码器（Variational AutoEncoder, VAE）

二：常见神经网络简介

本文主要是基于两种神经网络进行自编码降维，一个就是一般的反向传播神经网络，另一种就是卷积神经网络。

• 一般反向传播神经网络（BPNN）

图2

如上面图2显示，BPNN可以说是比较经典的入门神经网络，相关介绍是非常多的，总的来说就是正向向前得出预测值，根据误差函数和优化器来进行反向链式法则求导以更新各种权重参数。本人在此篇文章也介绍过基于LSTM网络的参数更新理论推导，这里BPNN就不过多介绍了。有兴趣的可以看看这里：LSTM的理论与实验

• 卷积神经网络（CNN）

由于卷积神经网络算是比较经典和熟悉的网络结构，大体前项顺序为：数据输入层、卷积计算层、ReLU激励层、池化层、全连接层（FC），反向参数更新依旧根据建立loss函数、链式法则求导以及梯度下降算法，下面我们简单回顾总结下：

1. 数据输入层：对建模数据进行简单的预处理，包括但不限于异常值处理，标准化处理等等，
2. 卷积计算层：通过设定滑动窗口的过滤器，通过卷积计算公式对数据进行特征提取，每个神经元一般只提取一种特征且一次权重值是不变的，即所谓权重共享机制，
3. 激励层：即把卷积层的结果做非线性映射，用公式可以表示为：$output=f\left({\sum }_i^n{w}_i{x}_i+b\right)$，这里 $f$ 就是所谓的激活函数，
4. 池化层：池化层夹在连续的卷积层中间，
   用于压缩数据和参数的量，减小过拟合。简而言之，如果输入是图像的话，那么池化层的最主要作用就是压缩图像，
5. 全连接层：两层之间所有神经元都有权重连接，通常全连接层在卷积神经网络尾部。也就是跟传统的神经网络神经元的连接方式是一样的，
6. 反向传播更新参数：设真实值与预测值误差为 $E=\frac{1}{2}{\sum }_{i=1}^N{\left(Y_i-T_i\right)}^2$ ，其中共 $N$ 个训练样本，那么再根据链式法则对参数 $w_i,b_i$ 求导以及梯度下降算法即可更新每个参数！

PS：以上过程仅仅对CNN结构做浓缩总结！

三：基于BPNN的自编码降维实验

from keras.layers import MaxPooling1D,Conv1D,UpSampling1D
from keras.layers import Dense, Input
from keras.models import Model
from keras import initializers
import matplotlib.pyplot as plt
import tensorflow as tf
import numpy as np
import pandas as pd
import time

my_seed = 999###
tf.random.set_seed(my_seed)##运行tf这段才能真正固定随机种子

plt.rcParams['font.sans-serif']=['SimHei']##中文乱码问题！
plt.rcParams['axes.unicode_minus']=False#横坐标负号显示问题！

originaldata = pd.read('建模数据.xlsx',index_col=0)

def data_format(data):

    data = (data - data.min()) / (data.max() - data.min())  ### minmax_normalized
  # data = (data - data.mean()) / data.std()  ### standarded_normalized
    data = np.array(data)##从矩阵形式转换数组形式
    return data
x_all_normalize = data_format(originaldata)

def bulid_BPNNmodel(train_data, test_data):

    ##压缩特征维度
    encoding_dim = 10
    input_msg = Input(shape=(train_data.shape[1],))

    # 编码层
    h1 = 128  ##隐藏层1
    h2 = 64  ##隐藏层2
    h3 = 32  ##隐藏层3
    encoded = Dense(h1, activation='relu', kernel_initializer=initializers.random_normal(stddev=0.01),bias_initializer='zeros')(input_msg)
    encoded = Dense(h2, activation='relu', kernel_initializer=initializers.random_normal(stddev=0.01),bias_initializer='zeros')(encoded)
    encoded = Dense(h3, activation='relu', kernel_initializer=initializers.random_normal(stddev=0.01),bias_initializer='zeros')(encoded)
    encoder_output = Dense(encoding_dim)(encoded)

    # 解码层
    decoded = Dense(h3, activation='relu', kernel_initializer=initializers.random_normal(stddev=0.01),bias_initializer='zeros')(encoder_output)
    decoded = Dense(h2, activation='relu', kernel_initializer=initializers.random_normal(stddev=0.01),bias_initializer='zeros')(decoded)
    decoded = Dense(h1, activation='relu', kernel_initializer=initializers.random_normal(stddev=0.01),bias_initializer='zeros')(decoded)
    decoded_output = Dense(train_data.shape[1], activation='relu',kernel_initializer=initializers.random_normal(stddev=0.01), bias_initializer='zeros')(decoded)

    autoencoder = Model(inputs=input_msg, outputs=decoded_output)  # 解码
    encoder_model = Model(inputs=input_msg, outputs=encoder_output)  # 编码
    autoencoder.compile(optimizer='adam', loss='mean_squared_error', metrics=['mse'])

    print(train_data.shape, input_msg.shape, decoded_output.shape, encoder_output.shape)
    bs = int(len(train_data) / 4)  #####数据集较少，全参与形式，epochs一般跟batch_size成正比
    epochs = max(int(bs / 2), 128 * 3)##最少循环128次
    a = autoencoder.fit(train_data, train_data, epochs=epochs, batch_size=bs, verbose=0, validation_split=0.2)##在训练集中划分0.2作为测试集
    print('训练集Loss列表（长度%s）%s：' % (len(a.history['loss']), a.history['loss']))
    print('测试集Loss列表（长度%s）%s：' % (len(a.history['val_loss']), a.history['val_loss']))
    print('\033[1;31m{0:*^80}\033[0m'.format('测试集损失函数值情况'))
    print(autoencoder.evaluate(test_data, test_data))  ##观察测试集损失情况
    # encoder_model.save('临时保存的BPNN模型.hdf5')
    return encoder_model,bs,a.history['loss'],a.history['val_loss']

###预测和作图
def outputresult(data,model):
    modelres = model(data,data)
    dim_msg = modelres[0].predict(data)##此时预测是拿纯测试集预测
    print('降维后数据维度：',dim_msg.shape)
    dim_msg = np.reshape(dim_msg,(dim_msg.shape[0],dim_msg.shape[1]))
    latent_feature = pd.DataFrame(dim_msg)
    latent_feature.index = originaldata.index##read_res[2]
    latent_feature.columns = [('feature'+str(i + 1)) for i in range(dim_msg.shape[1])]
    latent_feature = np.round(latent_feature,6)
    print(latent_feature)

    plt.figure(figsize=(15, 8))
    plt.plot(modelres[2], label='训练集损失',)
    plt.plot(modelres[3], label='测试集损失')
    plt.xlabel('循环次数',fontsize=18)
    plt.tick_params(labelsize=18)
    plt.legend(fontsize=15)
    plt.show()
    return x_all_normalize.shape
outputresult(x_all_normalize,bulid_BPNNmodel)

图3

四：基于CNN的自编码降维实验

##只需要调用的时候把bulid_BPNNmodel改为bulid_CNNmodel即可

def bulid_CNNmodel(train_data, test_data):

    fnum1 = 16  ##filter1数目
    fnum2 = 1  ##filter2数目，如果最后一层是多卷积核，那么将出现多个平行降维数据，我们可以取其中一个，或者均值，或者直接设定一个卷积核
    ps1 = 25  ##pool_size1##这里的pooling要注意，因为存在整数运算逻辑，如果我们一维数据维度大小为1024，那么1024/25/10非正整数，将报错
    ps2 = 10  ##pool_size2##如果是2050，则降维后一维数据维度为2500/25/10=10
    input_msg = Input((train_data.shape[1], 1))
    encoded = Conv1D(filters=fnum1, kernel_size=4, strides=1, padding='same', activation='tanh',kernel_initializer=initializers.random_normal(stddev=0.01), bias_initializer='zeros')(input_msg)
    encoded = MaxPooling1D(pool_size=ps1)(encoded)
    encoded = Conv1D(filters=fnum2, kernel_size=6, strides=1, padding='same', activation='tanh',kernel_initializer=initializers.random_normal(stddev=0.01), bias_initializer='zeros')(encoded)
    encoder_output = MaxPooling1D(pool_size=ps2)(encoded)
    encoder_model = Model(inputs=input_msg, outputs=encoder_output)

    # 解码器，反过来
    decoded = UpSampling1D(size=ps2)(encoder_output)##上采样过程（反卷积）
    decoded = Conv1D(filters=fnum1, kernel_size=6, strides=1, padding='same', activation='tanh',kernel_initializer=initializers.random_normal(stddev=0.01), bias_initializer='zeros')(decoded)
    decoded = UpSampling1D(size=ps1)(decoded)
    decoded = Conv1D(filters=fnum2, kernel_size=4, strides=1, padding='same', activation='tanh',kernel_initializer=initializers.random_normal(stddev=0.01), bias_initializer='zeros')(decoded)

    # 转成原始数据大小
    decoded_output = Conv1D(filters=1, kernel_size=2, strides=1, padding='same', activation='tanh',kernel_initializer=initializers.random_normal(stddev=0.01), bias_initializer='zeros')(decoded)
    autoencoder = Model(input_msg, decoded_output)
    print(autoencoder.summary())  ##打印网络结构
    autoencoder.compile(optimizer='adam', loss='mean_squared_error', metrics=['mse'])

    print(train_data.shape, input_msg.shape, decoded_output.shape, encoder_output.shape)
    bs = int(len(train_data) / 4)  #####数据集较少，全参与形式，epochs一般跟batch_size成正比
    epochs = max(int(bs / 2), 128 * 3)
    a = autoencoder.fit(train_data, train_data, epochs=epochs, batch_size=bs, verbose=0, validation_split=0.2)##在训练集中划分0.2作为测试集
    print('训练集Loss列表（长度%s）%s：' % (len(a.history['loss']), a.history['loss']))
    print('测试集Loss列表（长度%s）%s：' % (len(a.history['val_loss']), a.history['val_loss']))
    print('\033[1;31m{0:*^80}\033[0m'.format('测试集损失函数情况'))
    print(autoencoder.evaluate(test_data, test_data))  ##观察测试集损失情况
    # encoder_model.save('临时保存的CNN模型.hdf5')
    return encoder_model,bs,a.history['loss'],a.history['val_loss'],autoencoder

图4

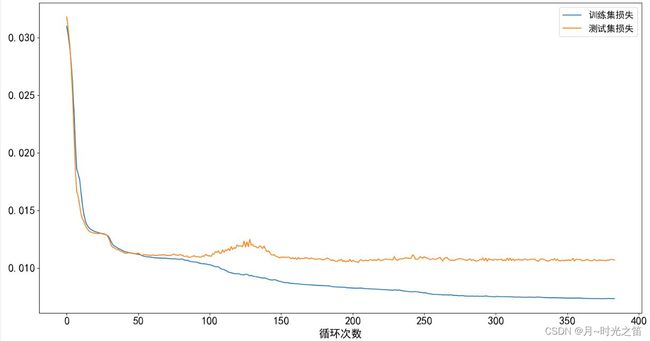
对比图1和图2我们能明显感受到CNN基于训练集构成的降维模型在测试集上的表现要比BPNN好，也许是因为基于卷积和反卷积操作提取和还原信息更为详细和清晰的缘故，但付出的代价是训练时间明显要长于BPNN，本人这台PC机如果BPNN需要26s，CNN大约需要95s，约3.7倍！

五：总结

自编码器属于神经网络的另一种用途。当然自编码器运用的神经网络不仅仅限于BPNN、CNN，RNN类型的网络同样能运用。但是，每个模型并不是万能的，自编码同样有一些缺点，比如在过拟合处理方面，我们要异常的小心处理，否则“学习的方向”很容易出现误导性错误。