带马尔科夫切换的正向随机微分方程数值格式模拟

前言

在现实世界中, 很多现象或模型都具有状态切换的特性, 用马尔科夫链刻画这一现象, 可以很好地解释不同条件下的随机切换，这导致马尔科夫切换的随机微分方程（SDEwMS）在最近几年的迅速发展。这种随机数学模型不仅能广泛运用于金融市场，而且在控制工程领域同样如此。然而这类模型的显式解是非常难求的，我们此篇文章主要是建立弱一阶Euler和Milstein格式来求解此类随机微分方程，想要了解更高解的弱格式，可以参考如下论文。

Yang Li, Taitao Feng, Yaolei Wang, and Yifei Xin. A high order accurate and effective scheme for solving Markovian switching stochastic models[J]. Mathematics, 2021, 9(6), 588.

一：带马尔科夫切换的随机微分方程（SDEwMS）

1：马尔科夫链知识

- 基础的跳和马尔科夫链知识

在之前的“随机知识”相关文章中，我们详细提到了马氏链以及如何模拟离散马氏链的相关知识，详细可见如下文章，这里不再介绍，但后面的格式模拟会用到此部分知识。
离散马氏链模拟过程

• 泊松随机测度

结合基础知识，我们定义 $N(de,dt)$ 为在空间 $\epsilon \times [0,T]$ 上的强度为 $\lambda (de)dt$

的泊松随机测度，其中 $\lambda$ 为在$\epsilon$ 上的$Lebanese$测度，

有 $d{r}_t={\int }_{\epsilon }l(r_{t-,},e)N(de,dt)$ ，其中 $l(i,e)=j-i,e\in {\Delta }_{ij};l(i,e)=0$, 其他，

其中 ${\Delta }_{ij}$ 是长度 跟$q_{ij}$ 有关的小区间，定义如下：

${\Delta }_{12}=[0,q_{12}),{\Delta }_{13}=[q_{12},q_{12}+q_{13}),...,{\Delta }_{1M}$

${\Delta }_{12}=[0,q_{12}),{\Delta }_{13}=[q_{12},q_{12}+q_{13}),...,$

${\Delta }_{1M}=\left[{\sum }_{j=2}^{M-1}{q}_{1j},{\sum }_{j=2}^M{q}_{1j}\right),$

${\Delta }_{21}=\left[{\sum }_{j=2}^M{q}_{1j},{\sum }_{j=2}^M{q}_{1j}+q_{21}\right),$

${\Delta }_{23}=\left[{\sum }_{j=2}^M{q}_{1j}+q_{21},{\sum }_{j=2}^M{q}_{1j}+q_{21}+q_{23}\right),..,$

${\Delta }_{2M}=\left[{\sum }_{j=2}^M{q}_{1j}+{\sum }_{j=1,j\ne 2}^{M-1}{q}_{2j},{\sum }_{j=2}^M{q}_{1j}+{\sum }_{j=1,j\ne 2}^M{q}_{2j}\right),...$

$=\left[{\sum }_{j=2}^{M-1}{q}_{1j},{\sum }_{j=2}^M{q}_{1j}\right),$

${\Delta }_{21}=\left[{\sum }_{j=2}^M{q}_{1j},{\sum }_{j=2}^M{q}_{1j}+q_{21}\right),$

${\Delta }_{23}=\left[{\sum }_{j=2}^M{q}_{1j}+q_{21},{\sum }_{j=2}^M{q}_{1j}+q_{21}+q_{23}\right),..,$

${\Delta }_{2M}=\left[{\sum }_{j=2}^M{q}_{1j}+{\sum }_{j=1,j\ne 2}^{M-1}{q}_{2j},{\sum }_{j=2}^M{q}_{1j}+{\sum }_{j=1,j\ne 2}^M{q}_{2j}\right),...$

其中 $M$ 是马氏链长度。

2：SDEwMS的结构介绍

在完备概率空间 $\left(\Omega ,F,P\right)$ ，具有信息流 ${\left\{F_t\right\}}_{t\ge 0}$ ，一般$SDEwMS$有如下微分结构：

$d{X}_t=f(t,X_t,r_t^h)dt+g(t,X_t,r_t^h)d{W}_t,t\in (0,T],X_0=x_0$。

其中 $T$ 是一个有限的终端时刻， $r_t^h\in S=\{1,2,...,M\}$ 为右连续的$Borel$可测的马尔科夫链。

$W_t={\left(W_t^1,...,W_t^d\right)}^T$ 是 $d$ 维各元素之间互相独立的布朗运动，

$X_t={\left(X_t^1,...,X_t^q\right)}^T$ 是 $q$ 维随机过程，漂移项 $f(\cdot ,\cdot ,\cdot ,):[0,T]\times R^q\times S\to R^q$ 和

扩散项 $g(\cdot ,\cdot ,\cdot ,):[0,T]\times R^q\times S\to R^{q\times d}$ 都是可测函数， $x_0$ 是方程的初始值。

3：解的存在唯一性定理

对固定常数 $L$ 和任意有限的终端时刻， $T>0,x,y\in R^q,\forall t\in [0,T]$, 飘逸系数

$f(\cdot ,\cdot ,\cdot ,)$ ，扩散系数 $g(\cdot ,\cdot ,\cdot ,)$ 满足$Lipschitz$ 条件：

$\left|f(t,x,i)-f(t,y,i)\right|\vee \left|g(t,x,i)-g(t,y,i)\right|\le L\left|x-y\right|,\left|f(t,x,i)-f(s,x,i)\right|\le L\left|t-s\right|$。
及线性增长条件：

$\left|f(t,x,i)\vee g(s,x,i)\right|\le M(1+\left|x\right|)$ ，

其中 $M=L\vee max\{\left|f(t,0,i)\vee g(t,0,i)\right|\}$。

所以方程$SDEwMS$满足如上条件，当初始条件 $x_0\in F_0$ 时，方程存在唯一的解

$\{X_t,t\in [0,T]\}$ 。

具体证明可参阅相关论文文献！

二：相关伊藤公式

伊藤公式是推导相关数值格式的必要理论知识，所以这里要详细介绍一下。

1：伊藤公式

对上述$SDEwMS$方程，我们记 $x\in R^q,\phi (t,x,i)\in C^{2,1}\left([0,T]\times R^q\times S;R\right)$ ，定义算子

$L^0\phi ,L^j\phi ,L_e^{-1}\phi$ 从 $R^q\times S\to R:L_{\phi }^0=\frac{\partial \phi }{\partial t}+{\sum }_{k=1}^q\frac{\partial \phi }{\partial x_k}{f}_k+\frac{1}{2}{\sum }_{m=1}^d{\sum }_{l,k=1}^q\frac{{\partial }^2\phi }{\partial x_k\partial x_l}{g}_{l,m}{g}_{k,m}$

$+{\sum }_{j\in S}{q}_{ij}\phi$,

$L^j\phi ={\sum }_{k=1}^q\frac{\partial \phi }{\partial x_k}{g}_{k,j},L_e^{-1}\phi =\phi \left(t,x,i+l(i,e)\right)-\phi (t,x,i)$,

其中 $i\in S,i\le j\le d$。

我们得到如下伊藤积分公式：

$\phi \left(t_{n+1},X_{t_{n+1}},r_{t_{n+1}}\right)=\phi (t_n,X_{t_n},r_{t_n})+{\int }_{t_n}^{t_{n+1}}{L}^0\phi (s,X_s,r_s)ds+$

${\sum }_{j=1}^d{\int }_{t_n}^{t_{n+1}}{L}^j\phi (s,X_s,r_s)d{W}_s^j+{\int }_{t_n}^{t_{n+1}}{\int }_{\epsilon }{L}_e^{-1}\phi \left(s,X_s,r_s\right)\tilde{N}(de,ds)$，

这里 $\tilde{N}(de,ds)=N(de,ds)-\lambda (de)ds$ 是一个补偿泊松测度。

2：伊藤展开

结合上述的伊藤公式算子，对任意 $\phi \left(t_{n+1},X_{t_{n+1}},r_{t_{n+1}}\right)\in C^{2,1}(R^q\times S;R)$ ，在 t_n 处使用伊藤公式得到如下积分形式：

$\phi \left(t_{n+1},X_{t_{n+1}},r_{t_{n+1}}\right)=\phi \left(t_n,X_{t_n},r_{t_n}\right)+{\int }_{t_n}^{t_{n+1}}{L}^0\phi \left(s,X_s,r_s\right)ds+$

${\sum }_{j=1}^d{\int }_{t_n}^{t_{n+1}}{L}^j\phi \left(s,X_s,r_s\right)d{W}_s^j$,

为了简化叙述伊藤展开，我们令 $d=q=1$ ，同理得：

$\phi \left(t_{n+1},X_{t_{n+1}},r_{t_{n+1}}\right)=\phi \left(t_n,X_{t_n},r_{t_n}\right)+{\int }_{t_n}^{t_{n+1}}{L}^0\phi \left(s,X_s,r_s\right)ds+{\int }_{t_n}^{t_{n+1}}{L}^1\phi \left(s,X_s,r_s\right)d{W}_s$,

我们再对 $L^0\phi \left(s,X_s,r_s\right)和L^1\phi \left(s,X_s,r_s\right)$ 使用伊藤公式可得：

$\phi \left(t_{n+1},X_{t_{n+1}},r_{t_{n+1}}\right)=\phi \left(t_n,X_{t_n},r_{t_n}\right)+$

${\int }_{t_n}^{t_{n+1}}\left[L^0\phi \left(s,X_s,r_s\right)+{\int }_{t_n}^s{L}^0{L}^0\phi \left(\tau ,X_{\tau },r_{\tau }\right)d\tau +{\int }_{t_n}^s{L}^1{L}^0\phi \left(\tau ,X_{\tau },r_{\tau }\right)d{W}_{\tau }+{\int }_{t_n}^s{L}_e^{-1}{L}^0\phi \left(\tau ,X_{\tau },r_{\tau }\right)d{\tilde{N}}_{\tau }\right]ds+$

${\int }_{t_n}^{t_{n+1}}\left[L^1\phi \left(s,X_s,r_s\right)+{\int }_{t_n}^s{L}^0{L}^1\phi \left(\tau ,X_{\tau },r_{\tau }\right)d\tau +{\int }_{t_n}^s{L}^1{L}^1\phi \left(\tau ,X_{\tau },r_{\tau }\right)d{W}_{\tau }+{\int }_{t_n}^s{L}_e^{-1}{L}^1\phi \left(\tau ,X_{\tau },r_{\tau }\right)d\tilde{N}\tau \right]d{W}_s$。

在得到上面等式中, 若 $\phi \left(s,X_s,r_s\right)$ 足够光滑, 我们继续对上述涉及的多维积分展开, 可以得到更高阶的数值格式。

三：数值格式

1：弱收敛定义

给定时间分割 $0=t_0<t_1<...<t_{N-1}<t_N=T$ ，假设 $\Delta t=t_{n+1}-t_n,\Delta W_n=W_{t_{n+1}}-$

$W_{t_n}(n=0,1,2,...,N)$, 且存在光滑函数 $G\in C_p^{2(\beta +1)}$ 和正常数 $C$ 满足不等式

$\left|E[G(X_t)-G(X^N)]\right|\le C\left(1+E[|X_0{|}^b]\right)(\Delta t{)}^{\beta }$,

其中 $\beta ,b\in N$ ,则 $X^N$ 以阶数 \beta 弱收敛于 $X_T$。 当然有弱收敛就有强收敛，当我们不以整个轨迹误差取期望再绝对值，取而代之的是以每个点的绝对误差取期望后，就是我们的强收敛误差要求，高阶强收敛格式更加复杂，条件更加苛刻，阶数可以是0.5的倍数关系。

2：弱一阶收敛格式

我们简记 $f_k^i=f(t,X^n,i),g_k^i=g(t,X^n,i)$ , 于是有如下格式:
设初始条件 $X_0$ 已知，对于 $0\le n\le N-1$ ，对于 $m$ 维的伊藤过程的第 $k$ 个分量，我们有如下格式：

1：欧拉格式（弱1.0阶，强0.5阶）： $X_k^{n+1,i}=X_k^n+f_k^i\Delta t+g_k^i\Delta W_n$
2：米尔斯坦格式（强弱都是1.0阶）： $X_k^{n+1,i}=X_k^n+f_k^i\Delta t+g_k^i\Delta W_n+\frac{1}{2}{L}^1{g}_k^i\left((\Delta W_n{)}^2-\Delta t\right)$
3：高阶收敛格式

高阶格式的形式比较复杂，且模拟和证明难度较大，想要了解更高解的弱格式，可以参考如下论文。

Yang Li, Taitao Feng, Yaolei Wang, and Yifei Xin. A high order accurate and effective scheme for solving Markovian switching stochastic models[J]. Mathematics, 2021, 9(6), 588.

四：实验模拟

• 马尔科夫链代码

import matplotlib.pyplot as plt
import numpy as np
import time
plt.rcParams['font.sans-serif']=['SimHei']##中文乱码问题！
plt.rcParams['axes.unicode_minus']=False#横坐标负号显示问题！

start_time = time.time()

def markov_m(days,delta):
    original_value = 1  ## 设置初始状态
    r = np.array([[-1,0.6,0.4], [10 ,-5, 5], [3, 1, -4]])  ###根据定义随意给的的转移速率矩阵
    p = r * delta
    for i in range(r.shape[1]):
        p[i, i] = 1 + p[i, i]

    # P = np.exp(delta * r) - 1
    # for i in range(r.shape[1]):
    #     P[i, i] = 1 + P[i, i]
    # print(P)  ###delta越小，P跟p越接近

    U = np.random.uniform(0,1,days)
    q = np.zeros((1,days))

    for i in range(days):
        u = U[i]
        v_temp = original_value
        q[:,i] = v_temp
        original_value = 1
        s = 0
        while original_value <= p.shape[1] and u > s:
            s = s + p[v_temp - 1, original_value - 1]  ###概率值叠加
            original_value = original_value + 1  ###矩阵列索引变大
        original_value = original_value - 1  ##由于开始original_value =1，所以要减1
    return p,q.tolist()[0]

• SDEwMS格式模拟代码

def schemes(a_ls,b_ls,names):

    time_ls = [16,32,64,128,256]
    tran_matx_ls = []
    state_vect_ls = []
    for i in time_ls:
        mres = markov_m(i, 0.1)##调用马氏链模拟函数
        tran_matx = mres[0]
        state_vect = mres[1]
        print('\033[1;31m时间长度为%s时转移概率矩阵为：\033[0m'%i)
        print(tran_matx)
        tran_matx_ls.append(tran_matx)
        print('\033[1;34m时间长度为%s时状态向量为：\033[0m'%i)
        print(state_vect)
        state_vect_ls.append(state_vect)

    logtimels = []
    logerrorls = []
    CRls = []
    msg = '''
                        1：exp函数
                        2：sin函数
                        3：原函数的2.5次方
                        4：原函数
                '''
    print(msg)
    msg_ls = ['exp函数','sin函数','原函数的2.5次方','原函数']
    ##定义初始化内容
    choose = int(input('请选择g(x)函数：'))
    echoes = 500
    error_ls = []
    value_matx = np.zeros((echoes,len(time_ls)))

    Euler = 'y + a * dt * y + b * y * dwt_temp'
    Milstein = Euler + ' + 0.5 * b * b * y * (dwt_temp * dwt_temp - dt)'
    schemes_ls = [Euler,Milstein]

    x0 = 1.5  ##SDE真解初始值
    for s,n in zip(schemes_ls,names):
        for e in range(echoes):
            for i in range(len(time_ls)):
                y = x0  ##数值格式初始值
                N = time_ls[i]
                dt = 1 / N
                yt = []
                dwt = np.random.normal(0,1,N) * np.sqrt(dt)
                nowstate_vect = state_vect_ls[i]

                ###真解求解过程
                v_ls = []
                vtemp = 0
                for j in range(N):##循环长度
                    a = a_ls[int(nowstate_vect[j] - 1)]##取对应的mu系数
                    b = b_ls[int(nowstate_vect[j] - 1)]##取对应的sigm系数
                    vtemp = vtemp + (a - 0.5 * b * b) * dt + b * dwt[j]##对于离散可变系数，用积分定义求解其真解
                    v_ls.append(vtemp)

                xT = ''##分配个内存
                finv = x0 * np.exp(v_ls[-1])
                if choose == 1:
                    xT = np.exp(finv)
                if choose == 2:
                    xT = np.sin(finv)
                if choose == 3:
                    xT = np.power(finv,2.5)
                if choose == 4:
                    xT = finv

                ##数值格式解
                for j in range(N):
                    a = a_ls[int(nowstate_vect[j]-1)]##取对应的mu系数
                    b = b_ls[int(nowstate_vect[j]-1)]##取对应的sigm系数
                    dwt_temp = dwt[j]
                    y = eval(s)
                    if choose == 1:
                        yt.append(np.exp(y))
                    if choose == 2:
                        yt.append(np.sin(y))
                    if choose == 3:
                        yt.append(np.power(y,2.5))
                    if choose == 4:
                        yt.append(y)
                error_temp = yt[N - 1] - xT ##真解与数值解末端值作差
                error_ls.append(error_temp)
            value_matx[e,:] = error_ls
            error_ls = []
        error_fin = np.abs(sum(value_matx) / echoes)##弱收敛最终求期望
        log_time = np.log(1 / np.array(time_ls))
        log_error_fin = np.log(error_fin)
        CR = np.polyfit(log_time,log_error_fin,1)##一次多项式拟合
        print('\033[1;36m{0:*^80}\033[0m'.format('计算结果'))
        print('格式%s的误差绝对值期望为：%s'%(n,np.round(error_fin,6)))
        print('格式%s的弱收敛阶为：%s'%(n,round(CR[0],6)))
        logerrorls.append(np.round(log_error_fin,6))
        logtimels.append(log_time)
        CRls.append(round(CR[0],6))
    return logtimels,logerrorls,CRls,msg_ls[choose - 1]

statemu_ls = [1,0.8,0.9]##飘逸系数
statesigm_ls = [-0.1,0.2,0.05]##扩散系数
scheme_names = ['Euler', 'Milstein']
R = schemes(statemu_ls,statesigm_ls,scheme_names)

图1

图2

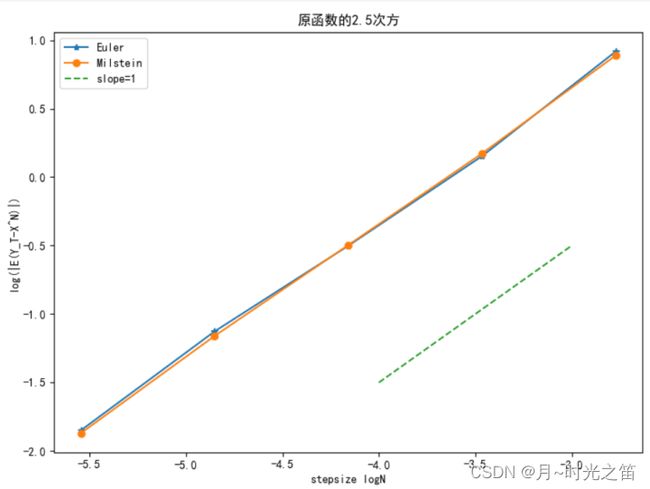
上图图1和图2就是模拟的实验结果，符合理论结果！

• 作图代码

marker_ls = ['-*','-o']
def make_figure():
    plt.figure(figsize=(8, 6))
    for i,j,l,m in zip(R[0],R[1],scheme_names,marker_ls):
        plt.plot(i,j,m,label=l)
    plt.plot(np.array([-4,-3]),np.array([-4,-3]) + 2.5,'--',label='slope=1')
    plt.xlabel('stepsize logN')
    plt.ylabel('log(|E(Y_T-X^N)|)')
    plt.title(R[3])
    plt.legend()
    plt.show()
make_figure()

图3

五：总结

SDEwMS是SDE的一个推广，试用性更强，但是对应的数值解理论会变得更加复杂。近年来，很多人也研究倒向带马尔科夫的随机微分方程并取得了很多理论上的突破。

随机微分方程是个很深很广的研究领域，无论正向还是倒向，无论带切换还是带跳还是带反射，都是值得研究的，有兴趣的朋友可以多研读这方面的著作，本篇内容仅抛砖引玉之用！