机器学习笔记之受限玻尔兹曼机(二)模型表示

引言

上一节基于马尔可夫随机场介绍了玻尔兹曼分布，本节将介绍受限玻尔兹曼机的模型表示(Representation)与 学习任务(Laerning)。

回顾：玻尔兹曼分布

基于Hammersley-Clifford定理，可以将马尔可夫随机场$\mathcal{G}$中关于随机变量集合的联合概率分布$\mathcal{P}(\mathcal{X})$表示为如下形式：
$$\mathcal{P}(\mathcal{X})=\frac{1}{\mathcal{Z}}\prod _{i=1}^{\mathcal{K}}{\psi }_i(x_{{\mathcal{C}}_i})$$
其中$x_{{\mathcal{C}}_i}(i=1,2,\cdots ,\mathcal{K})$表示极大团${\mathcal{C}}_i$中结点组成的随机变量集合；${\psi }_i(x_{{\mathcal{C}}_i})$表示极大团$x_{{\mathcal{C}}_i}$对应的势函数；$\mathcal{Z}$表示规范化因子。
由于势函数的恒正属性，因此通常将势函数使用能量函数进行表示：
$${\psi }_i(x_{{\mathcal{C}}_i})=\exp \left\{-\mathbb{E}[x_{{\mathcal{C}}_i}]\right\}i=1,2,\cdots ,\mathcal{K}$$
那么 基于能量函数表示的联合概率分布$\mathcal{P}(\mathcal{X})$被称作吉布斯分布，也称玻尔兹曼分布：
这里全部使用’玻尔兹曼分布‘进行描述。
$$\begin{array}{rl}\mathcal{P}(\mathcal{X})& =\frac{1}{\mathcal{Z}}\prod _{i=1}^{\mathcal{K}}\exp \left\{-\mathbb{E}[x_{{\mathcal{C}}_i}]\right\}\\ & =\frac{1}{\mathcal{Z}}\exp \left[-\sum _{i=1}^{\mathcal{K}}\mathbb{E}[x_{{\mathcal{C}}_i}]\right]\end{array}$$

此时的联合概率分布$\mathcal{P}(\mathcal{X})$明显是指数族分布的表示形式。
可以将$-{\sum }_{i=1}^{\mathcal{K}}\mathbb{E}[x_{{\mathcal{C}}_i}]$看作是’某权重矩阵‘$\mathcal{W}$与’极大团向量‘$x_{\mathcal{C}}=(x_{{\mathcal{C}}_1},x_{{\mathcal{C}}_2},\cdots ,x_{{\mathcal{C}}_{\mathcal{K}}}{)}^T$的线性组合。
$$\frac{1}{\mathcal{Z}}\exp \left[-\sum _{i=1}^{\mathcal{K}}\mathbb{E}[x_{{\mathcal{C}}_i}]\right]\Rightarrow \frac{1}{\mathcal{Z}}\exp [{\mathcal{W}}^T{x}_{\mathcal{C}}]$$
如果给能量函数$\mathbb{E}[x_{{\mathcal{C}}_i}](i=1,2,\cdots ,\mathcal{K})$一个准确描述的话，可以将$\mathbb{E}[x_{{\mathcal{C}}_i}]$描述为如下形式：
$$\mathbb{E}[x_{{\mathcal{C}}_i}]=-\left\{[x_{{\mathcal{C}}_i}{]}^T\mathcal{U}{x}_{{\mathcal{C}}_i}+b^T{x}_{{\mathcal{C}}_i}\right\}i=1,2,\cdots ,\mathcal{K}$$
其中$\mathcal{U}$表示模型参数的权重矩阵；$b$表示偏置向量。

个人理解：在花书(第20章)将随机变量集合$x$描述为一个$d$维的分布。为了简化运算，将每一维分布均设为’伯努利分布‘，从而将’能量函数‘描述为如下形式:
$$\mathbb{E}(x)=-x^T\mathcal{U}x-b^{T}x$$
回归文章示例，将$p$维随机变量$\mathcal{X}$表示为’若干个结点‘(可能有的结点内部包含一个随机变量，有的包含多个)，然后将这些结点归纳为$\mathcal{K}$个极大团$x_{{\mathcal{C}}_i}(i=1,2,\cdots ,\mathcal{K})$。可以将每个极大团中的随机变量看作是$\mathcal{X}$的一个子集，因而这里的表述没什么问题。欢迎小伙伴们交流讨论。

玻尔兹曼机

玻尔兹曼机(Boltzmann Machine,BM)示例表示如下：
蓝色结点表示观测变量，白色结点表示隐变量，下同。

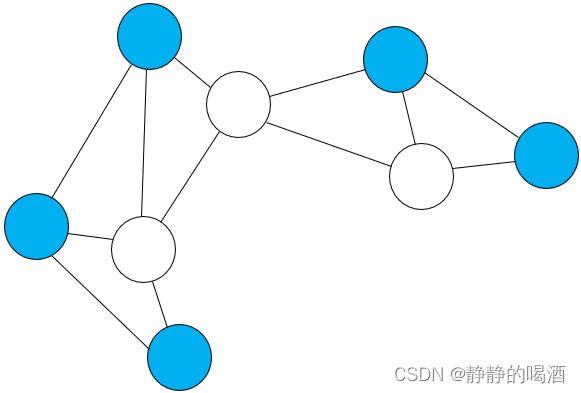
玻尔兹曼机本质上就是一个马尔可夫随机场，但是不同点在于玻尔兹曼机将随机变量集合$\mathcal{X}$分成了两个子集：
需要注意的是，这里的$m,n,p$表示随机变量的维度，而不是极大团的编号。
$$\begin{array}{rl}\mathcal{X}& =(x_1,x_2,\cdots x_p{)}^T\Rightarrow \left(\begin{array}{c}h\\ v\end{array}\right)\\ & \{\begin{array}{l}h=(h_1,h_2,\cdots ,h_m{)}^T\\ v=(v_1,v_2,\cdots ,v_n{)}^{T}m+n=p\end{array}\end{array}$$
其中$v$表示观测变量；$h$表示隐变量。它的能量函数不同于单个随机变量种类$x\in {\mathbb{R}}^p$，它的能量函数根据图中边两端结点种类 分为三种表示：
$$\mathbb{E}(v,h)=-\left[(v^T\mathcal{R}v+b^{T}v)+v^T\mathcal{W}h+(h^T\mathcal{S}h+c^{T}h)\right]$$

• 以观测变量$v$内部的边为例。$v_i,v_j\in v$表示观测变量的两个结点，它们之间的能量(边;关联关系)可表示为:
  $$\mathbb{E}(v_i,v_j)=-v_i\cdot r_{ij}\cdot v_j$$
  其中$r_{ij}$表示$v_i,v_j$之间的权重系数。至此，观测变量$v$内部的能量结果可表示为如下形式：
  $$\begin{array}{rl}-\sum _{i=1}^m\sum _{j=1}^m{v}_i\cdot r_{ij}\cdot v_j& =-(v_1,v_2,\cdots ,v_m)\left(\begin{array}{c}{r}_{11},r_{12},\cdots ,r_{1m}\\ r_{21},r_{22},\cdots ,r_{2m}\\ ⋮\\ r_{m1},r_{m2},\cdots ,r_{mm}\end{array}\right)\left(\begin{array}{c}{v}_1\\ v_2\\ ⋮\\ v_m\end{array}\right)\\ & =-v^T\mathcal{R}v\end{array}$$
• 其他表示边的关系如$-v^T\mathcal{W}h,-h^T\mathcal{S}h$同理。关于结点本身的能量也通过权重系数进行表达。如观测变量的能量表达：${\sum }_{i=1}^m{b}_i{v}_i=b^{T}v$,隐变量同理。

其中$\mathcal{R},b$表示基于观测变量团的权重矩阵和偏置向量；$\mathcal{S},c$表示基于隐变量团的权重矩阵和偏置向量；$\mathcal{W}$表示边两端分别是观测变量和隐变量的权重矩阵。
最终，玻尔兹曼机对应的 联合概率分布(概率质量函数) 表示如下：
在后续’玻尔兹曼机‘中将继续进行介绍。
$$\begin{array}{rl}\mathcal{P}(v,h)& =\frac{1}{\mathcal{Z}}\exp \{-\mathbb{E}[v,h]\}\\ & =\frac{1}{\mathcal{Z}}\exp \left\{\left[(v^T\mathcal{R}v+b^{T}v)+v^T\mathcal{W}h+(h^T\mathcal{S}h+c^{T}h)\right]\right\}\end{array}$$

关于玻尔兹曼机的问题

如果并不是所有变量都能够被观测，如隐变量的存在。这种情况下，隐变量类似于神经网络中的隐藏层神经元，此时的波尔兹曼机就不再局限于变量之间的线性关系了。通过对模型的学习，类似于神经网络隐藏层的函数逼近定理，它可以对 离散型随机变量的任意概率质量函数$\mathcal{P}(\mathcal{X})$进行逼近。

当然，这种情况下，同样需要玻尔兹曼机内部结点之间存在丰富的关联关系。如下图：

这种复杂结构引出玻尔兹曼机的缺陷：由于结构过于复杂，没有办法对其进行精确推断。
其次，如果使用近似推断，如马尔可夫链蒙特卡罗方法，由于分布过于复杂，需要采集足够量的样本对其进行近似。这种方式的计算量过于庞大。

受限玻尔兹曼机

玻尔兹曼机的缺陷主要在于模型对应的概率图结构过于复杂。受限玻尔兹曼机(Restricted Boltzmann Machine,RBM)是在玻尔兹曼机的基础上，对结点间的边进行约束。约束要求是：只有隐变量$h$和观测变量$v$之间存在连接，$h,v$变量内部无连接。

上图关于优化后的受限玻尔兹曼机表示如下：

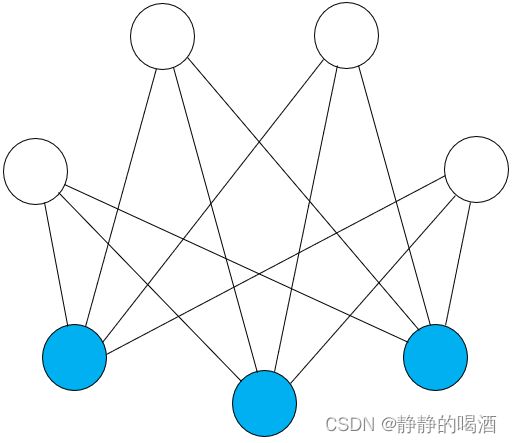
同理，基于改进后的概率图表达，可以对波尔兹曼机的联合概率分布进行优化：
$$\begin{array}{rl}\mathcal{P}(\mathcal{X})=\mathcal{P}(v,h)& =\frac{1}{\mathcal{Z}}\exp \{-\mathbb{E}(v,h)\}\\ & =\frac{1}{\mathcal{Z}}\exp (v^T\mathcal{W}h+b^{T}v+c^{T}h)\end{array}$$
继续对上式进行展开：
$$\begin{array}{rl}\mathcal{P}(v,h)& =\frac{1}{\mathcal{Z}}\exp [v^T\mathcal{W}h]\cdot \exp [b^{T}v]\cdot \exp [c^{T}h]\\ & =\frac{1}{\mathcal{Z}}\left\{\exp \left[\sum _{i=1}^m\sum _{j=1}^n{v}_i\cdot w_{ij}\cdot h_j\right]\cdot \exp \left[\sum _{i=1}^m{b}_i{v}_i\right]\cdot \exp \left[\sum _{j=1}^n{c}_j{h}_j\right]\right\}\\ & =\frac{1}{\mathcal{Z}}\left\{\prod _{i=1}^m\prod _{j=1}^n\exp (v_i\cdot w_{ij}\cdot h_j)\cdot \prod _{i=1}^m\exp (b_i{v}_i)\prod _{j=1}^n\exp (c_j{h}_j)\right\}\end{array}$$
上式展开后的结果就是各种各样的指数函数做乘法。因此可以从因子图(Factor Graph)的角度对受限玻尔兹曼机进行描述，对应因子图表示如下：
例如团(实际上就是极大团)$v_i\iff h_j$可以定义为$f_{ij}(v_i,h_j)=\exp (v_i\cdot w_{ij}\cdot h_j)$，其他同理。这里就不多描述了。
因受限玻尔兹曼机的性质，其概率图中任意三个结点之间均不能构成极大团。因此，每一条边对应的两个结点都是一个极大团。

最终，受限玻尔兹曼机需要学习的参数包含以下三个：
$$\mathcal{W}={\left(\begin{array}{c}{w}_{11},w_{12},\cdots ,w_{1n}\\ w_{21},w_{22},\cdots ,w_{2n}\\ ⋮\\ w_{m1},w_{m2},\cdots ,w_{mn}\end{array}\right)}_{m\times n}b={\left(\begin{array}{c}{b}_1\\ b_2\\ ⋮\\ b_m\end{array}\right)}_{m\times 1}c={\left(\begin{array}{c}{c}_1\\ c_2\\ ⋮\\ c_n\end{array}\right)}_{n\times 1}$$

受限玻尔兹曼机的学习任务(填坑)

在介绍对比散度(Contrastive Divergence)介绍完毕后，再介绍受限玻尔兹曼机的学习任务。

相关参考：
深度学习(花书)——第20章 深度生成模型
(系列二十八)玻尔兹曼机1-介绍
机器学习-受限玻尔兹曼机（3）-模型表示（Representation）