机器学习之四(读书笔记)
- Deep Learning
- Backpropagation
- Tips for Deep Learning
八、Deep Learning
历史:
- 1958:Perceptron(linear model)(感知器)
- 1969:Perceptron has limitation
- 1980:Multi-layer perceptron(多层感知器)(与今天的DNN没有显著差异)
- 1986:Backpropagation(反向传播)(通常超过3个隐藏层就train不出好的结果)
- 1989:1 hidden layer is “good enough”
- 2006:RBM initialization(breakthrough)(受限玻尔兹曼机的初始训练)
- 2009:GPU
- 2011:Deep Learning被引入到语音辨识中
- 2012:Deep Learning 赢得ILSVRC image比赛
Three Steps for Deep Learning:

- 第一步
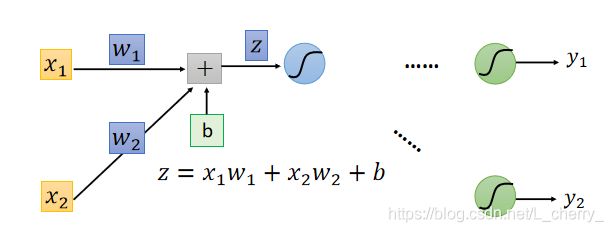
其中,第一步定义一个function,这个function就是一个Neural Network:
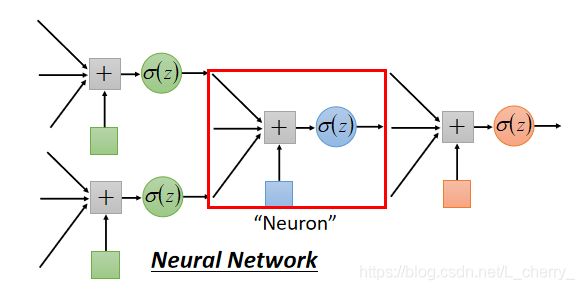
用不同的方法连接Neural Network就会得到不同的structure;Network的参数 θ \theta θ:所有neuron的weight和bias的集合。
连接Neuron的方式(自己手动设置):
Fully Connect Feedforward Network(最常见)(全连接前馈网络):
把Neuron拍成一排一排,每一组Neuron都有一组weight和bias(weight和bias是根据training data找出):

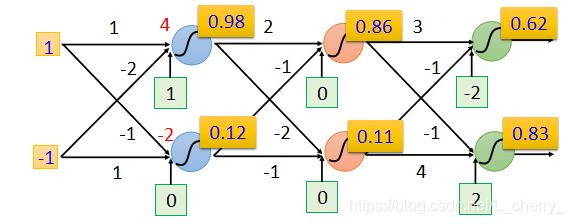
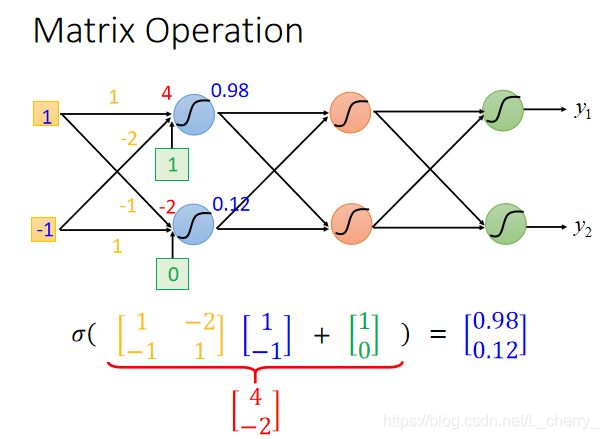
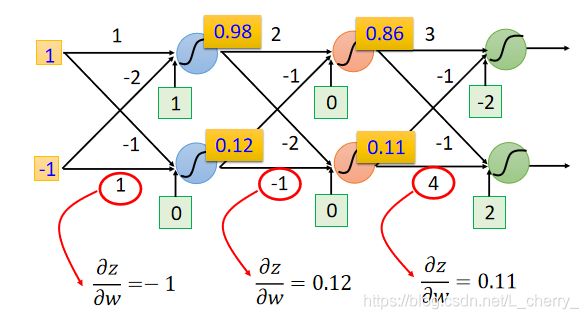
假设上面蓝色Neuron,w=1,-2;b=1;下面蓝色Neuron,w=-1,1;b=0;
假设现在的input是 [ 1 − 1 ] \begin{bmatrix} 1\\ -1 \end{bmatrix} [1−1],计算上面蓝色的Output为0.98
( 1 ∗ 1 + ( − 1 ) ∗ ( − 2 ) + 1 = 4 1*1+(-1)*(-2)+1=4 1∗1+(−1)∗(−2)+1=4再通过sigmoid function得到0.98,sigmoid function如下)
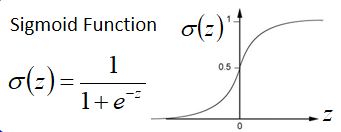
假设这个structure中的每一个weight和bias都已知,就可以反复进行以上运算,如下图:
假设input是 [ 0 0 ] \begin{bmatrix} 0\\ 0 \end{bmatrix} [00],得到的结果如下:
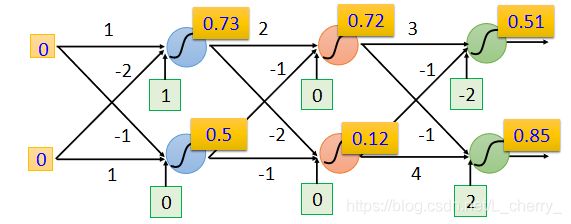
决定了一个Neural Network的structure就是决定了一个function set。
大体上,neuron有很多layer,layer和layer之间所有的Neuron两两相接,整个Network需要一组input(vector),对Layer1的每一个Neuron来说,它的input就是input layer 的每一个dimension:

其中,input layer不由neuron组成。
Deep = Many hidden layers,那么Deep Learning到底可以有几层hidden layer?
- AlexNet(2012):8 layers,错误率为16.4%
- VGG(2014):19 layers,错误率为7.3%
- GoogleNet(2014):22 layers,错误率为6.7%
- Residual Net(2015):152 layers,错误率为3.57%
network的运作常常把它用Matrix Operation(矩阵运算)来表示,举例:
假设第一个layer的两个neuron,它们的weight分别是1,-2,-1,1,即可排成一个matrix: [ 1 − 2 − 1 1 ] \begin{bmatrix} 1 &-2 \\ -1 & 1 \end{bmatrix} [1−1−21],假设input为 [ 1 − 1 ] \begin{bmatrix} 1\\ -1 \end{bmatrix} [1−1],bias为 [ 1 0 ] \begin{bmatrix} 1\\ 0 \end{bmatrix} [10],再通过sigmoid function得到结果,那么整个运算为:
在整个neural network文件中,sigmoid function被称为activation function(激活函数),但是不一定激活函数就是sigmoid function。
总体来说,一个neural network,假设第一个layer的weight全部集合起来成为一个矩阵 W 1 W^1 W1,bias全部集合起来当作一个向量 b 1 b^1 b1;同理,layer2的weight矩阵为 W 2 W^2 W2,bias向量为 b 2 b^2 b2…layerL的weight矩阵为 W L W^L WL,bias向量为 b L b^L bL,那么由input x得到output y的整个过程如下:
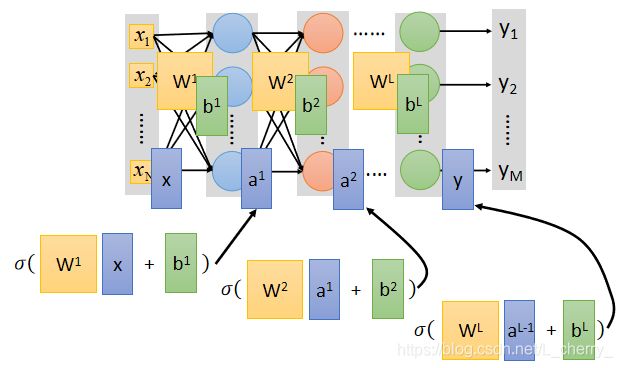
那么x和y的关系为:
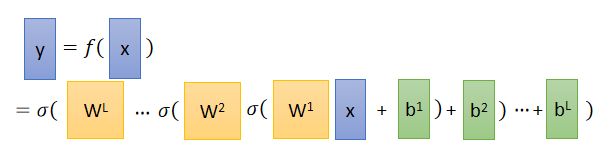
写成矩阵运算的好处是:可以用GPU加速。
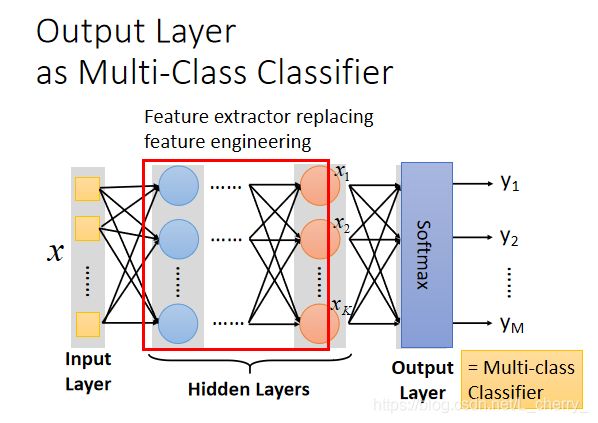
hidden layers可以看作feature extractor(特征提取器),代替了手工的feature engineering;
Output layer = Multi-Class Classifier,因此最后一layer会加上Softmax:
举例:识别手写数字
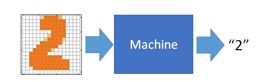
Input是一张图像,对机器来说,一张image就是一个vector(向量),假设这是一个解析度为16*16的image,那么它有256个pixel(像素),那么这个image就是一个256维的vector,每一个pixel对应其中一个dimension(维),涂黑的地方标记为1,没有涂黑的地方标记为0;
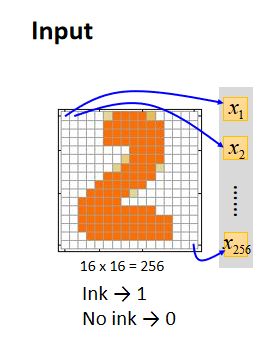
Output(这里是10维)看作是对应到每一个数字的几率,几率最大的数字为最终结果;
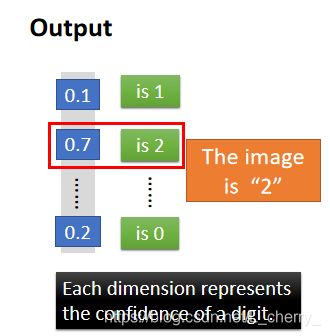
整个过程为:
接下来就是要使用Gradient Descent找一组参数,挑一个最适合用来实现手写数字辨别的function,在这个步骤里面需要做一些design(要求只有input256维,output 10维,需要设计几个hidden layer,每个hidden layer要有多少neuron)。
决定一个好的function set取决于这个network的structure。
Q:How many layers ?How many neurons for each layer?
Trial and Error + Intuition(直觉)
Q:Can the structure be automatically determined?
e.g. Evolutionary Artificial Neural Networks
Q:Can we design the network structure?
e.g. Convolutional Neural Network(CNN)
2.第二步
如何定义一个function的好坏?
假设做手写数字辨识,给定一组参数,现有一张image和它的label,通过label1得知target为一个10维的vector,第一维对应到数字1,其它维都对应到0;Input这张image的pixel,然后通过neural network得到一个Output,Output称之为 y y y,target称之为 y ^ \hat{y} y^,接下来计算这个 y y y和 y ^ \hat{y} y^的交叉熵(和做Multi-class classification一样),调整network的参数,使交叉熵越小越好。
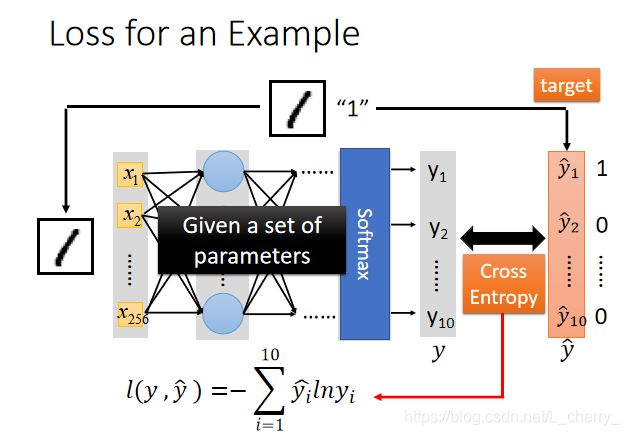
对于所有的training data而言,第一笔data算出来的cross entropy是 C 1 C^1 C1…第N笔data算出来的是 C N C^N CN,把所有的cross entropy加起来得到一个total loss L,接下来要在function set里找一个减少total loss L的function,或者找一组network的parameter θ ⋆ \theta^\star θ⋆减少total loss L。

怎么找一个 θ ⋆ \theta^\star θ⋆ minimize这个total loss?
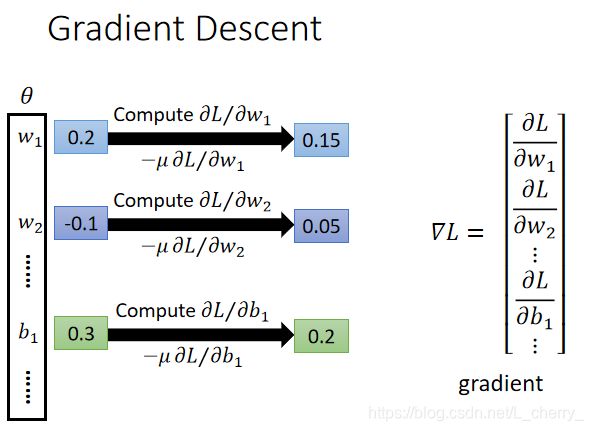
Grandient Descent
首先给 θ ⋆ \theta^\star θ⋆ 中的每一个参数random初始值,然后去计算一下每一个参数对total loss的偏微分,(把偏微分全部集合起来叫做Gradient)有了偏微分可以更新参数,得到一组新的参数,反复以上步骤得到一组好的参数。

Backpropagation:an efficient way to compute ∂ L / ∂ w \partial L/\partial w ∂L/∂w in neural network.
工具箱如下:

关于Backpropagation如何让Neural Network的training变得有效率
在其中用到一个知识点——Chain Rule(链规),如下图:
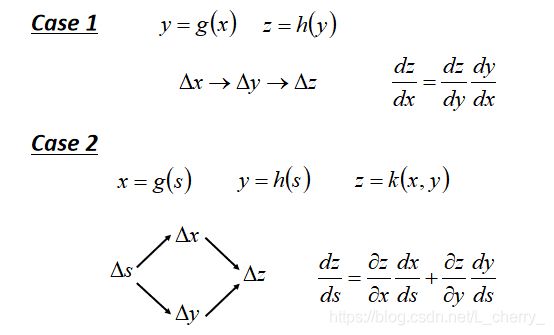
回到Neural Network的training:
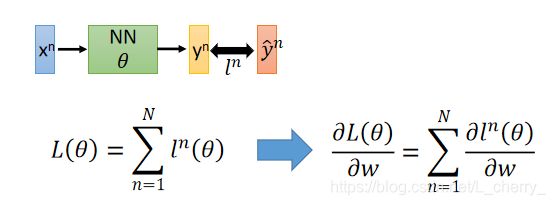
定义一个Loss Function,其中 l n l^n ln代表 y n y^n yn和 y ^ n \hat{y}^n y^n的距离(计算出每一笔data的偏微分,就可以得到total loss对w的偏微分):
首先考虑一个Neuron(如何计算它的偏微分):
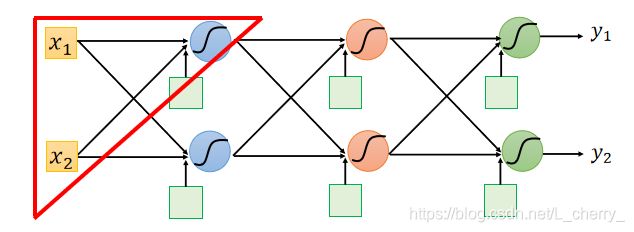
假设取layer1,那么它的偏微分为:

其中,计算所有参数的 ∂ z / ∂ w \partial z/\partial w ∂z/∂w叫做Forward pass(前传);计算用于所有输入z的激活函数的 ∂ l / ∂ z \partial l/\partial z ∂l/∂z叫做Backward pass(逆推);
- 计算 ∂ z / ∂ w \partial z/\partial w ∂z/∂w(Forward pass):
根据 z = x 1 w 1 + x 2 + w 2 + b z = x_1w_1+x_2+w_2+b z=x1w1+x2+w2+b得到:

结论:偏微分 ∂ z / ∂ w \partial z/\partial w ∂z/∂w的结果为由该权重w连接的输入值:
计算 ∂ l / ∂ z \partial l/\partial z ∂l/∂z(Backward pass):
假设这里的激活函数为sigmoid function,在layer1,令 a = σ ( z ) a =\sigma(z) a=σ(z) ,a乘上weight再加上一堆value得到 z ′ {z}' z′和 z ′ ′ {z}'' z′′ ,那么 ∂ l / ∂ z \partial l/\partial z ∂l/∂z:

那么 ∂ l / ∂ a \partial l/\partial a ∂l/∂a:
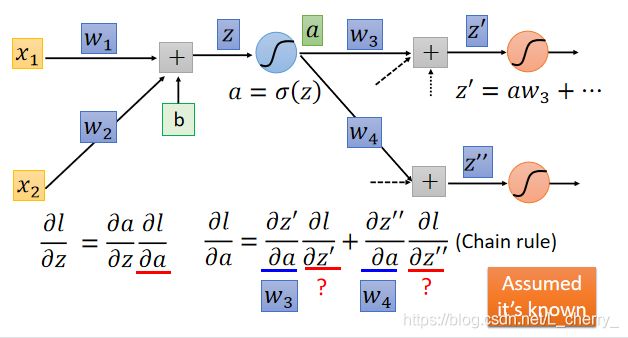
由于这里影响a的只有 z ′ {z}' z′和 z ′ ′ {z}'' z′′,所以计算 ∂ l / ∂ a \partial l/\partial a ∂l/∂a只有两项(如果有n个neuron就是有n项表达); ∂ z ′ / ∂ a \partial {z}'/\partial a ∂z′/∂a根据 z ′ = a w 3 + . . . {z}' = aw_3+... z′=aw3+...这个式子计算得到的值为 w 3 w_3 w3,同理, ∂ z ′ ′ / ∂ a = w 4 \partial {z}''/\partial a = w_4 ∂z′′/∂a=w4;
这里假设通过某种方法已经得到 ∂ l / ∂ z ′ \partial l/\partial {z}' ∂l/∂z′和 ∂ l / ∂ z ′ ′ \partial l/\partial {z}'' ∂l/∂z′′的值,那么 ∂ l / ∂ z \partial l/\partial z ∂l/∂z:
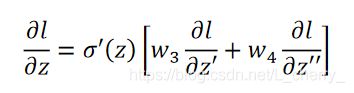
这里我们可以反向看待这个式子:假设有另外一个neuron,它的input就是 ∂ l / ∂ z ′ \partial l/\partial {z}' ∂l/∂z′和 ∂ l / ∂ z ′ ′ \partial l/\partial {z}'' ∂l/∂z′′,再分别乘上 w 3 w_3 w3和 w 4 w_4 w4相加后再乘以 σ ′ ( z ) {\sigma }'(z) σ′(z)得到output ∂ l / ∂ z \partial l/\partial z ∂l/∂z,其中 σ ′ ( z ) {\sigma }'(z) σ′(z)是一个常数。
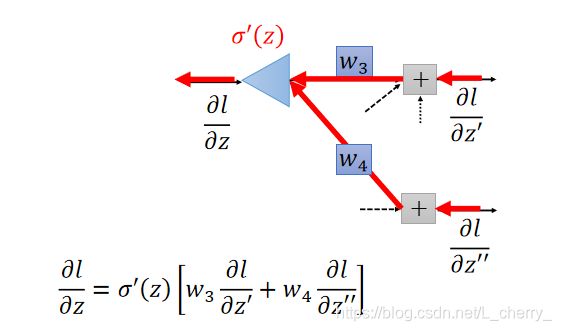
那么 ∂ l / ∂ z ′ \partial l/\partial {z}' ∂l/∂z′和 ∂ l / ∂ z ′ ′ \partial l/\partial {z}'' ∂l/∂z′′如何计算?
假设两个不同的case:
Case 1 :假设图中两个红色的Neuron就已经是Output Layer,那么 ∂ l / ∂ z ′ \partial l/\partial {z}' ∂l/∂z′和 ∂ l / ∂ z ′ ′ \partial l/\partial {z}'' ∂l/∂z′′就可以根据Chain Rule计算:
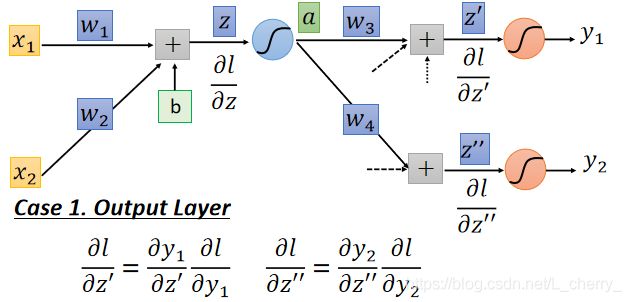
Case 2 :假设图中两个红色的Neuron不是Output Layer,后面还有其他东西,从最后一层往前算到此处:
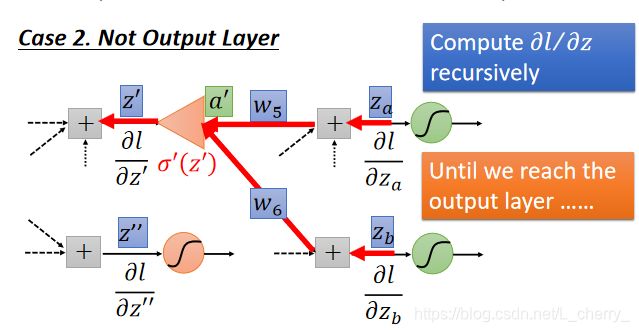
为了让整个计算有效率,应该从后往前算偏微分:
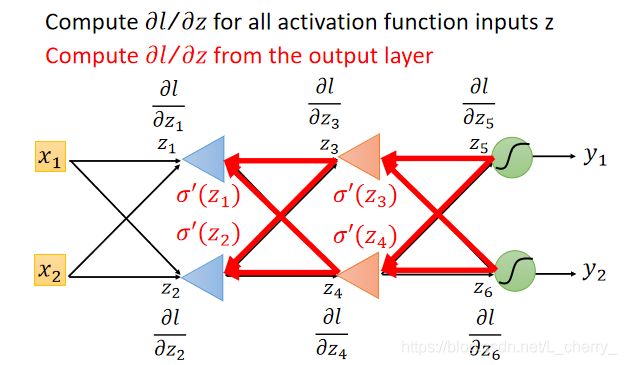
Backpropagation总结:
![]()
Why deep learning?
比较shallow和deep的model:
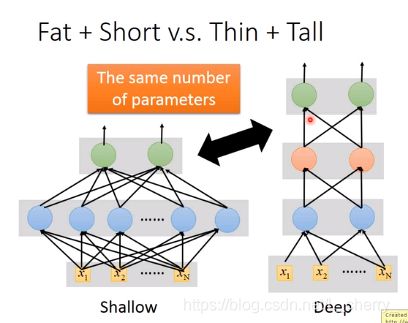
得到的结果是:
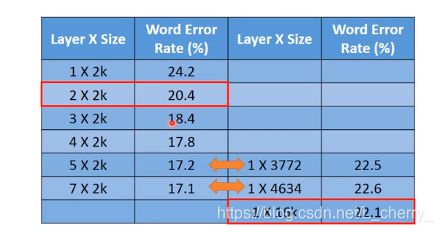
deep的效果较好的原因–可以将deep learning看成模块化(好处是有些function可以共享)。
假设现有短发女、短发男、长发女、长发男四类数据,由于长发男的数据较少导致长发男的classifier比较weak,就可以用模块化的概念解决这个问题:
(1)首先将这个问题切成比较小的问题,这样就会有足够的data去train出比较好的结果:
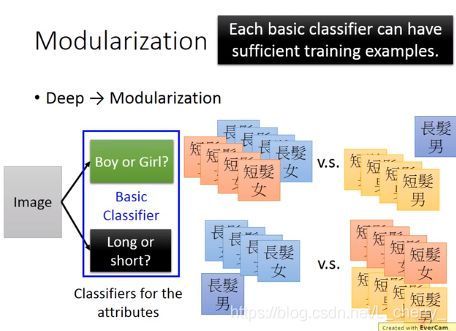
(2)最后解决这个问题时的classifier就去参考basic attribute output,这样每一个classifier共用同样的module,用比较少的数据也可以训练好:
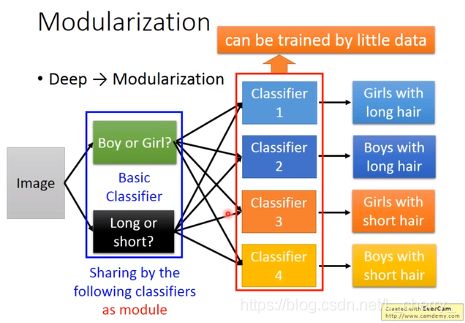
deep learning的modularization是自动学习的:
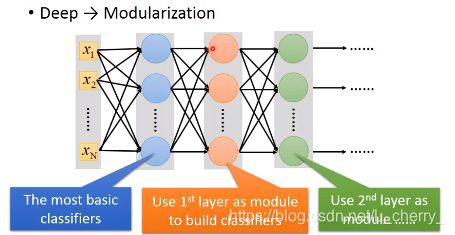
任何连续函数f可以用一层neuron network来完成,只要那一层neuron network够宽,但是这样是没有效率的,使用deep structure更有效率。
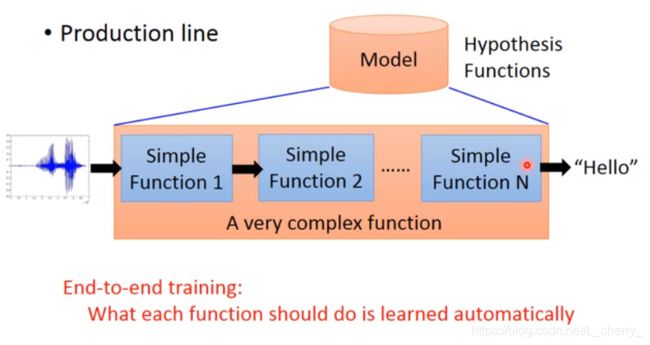
End-to end Learning:
假设要处理一个很复杂的Model,这个Model里面需要像一个生产线,由很多简单的function串联在一起,End-to end Learning就是只给Model的input,output,不需要告诉它中间的function 如何分工:
九、Tips for Deep Learning
完成Deep Learning的三步之后就会得到一个Neural Network,接着检查这个Neural Network在Training Data上有没有得到好的结果,如果没有,就返回检查之前的三步中有什么问题,思考如何修改可以在Training Data上得到比较好的结果;如果在Training Data上得到好的结果,就将结果imply到Testing Data上,如果在Testing Data上没有得到好的结果,那么就导致了过度拟合,仍然得返回检查之前的三步中有什么问题,再做修改;修改后再去检查Training Data上的结果是否变坏,如果变坏还得再去修改之前的三步,直至达到好的结果。
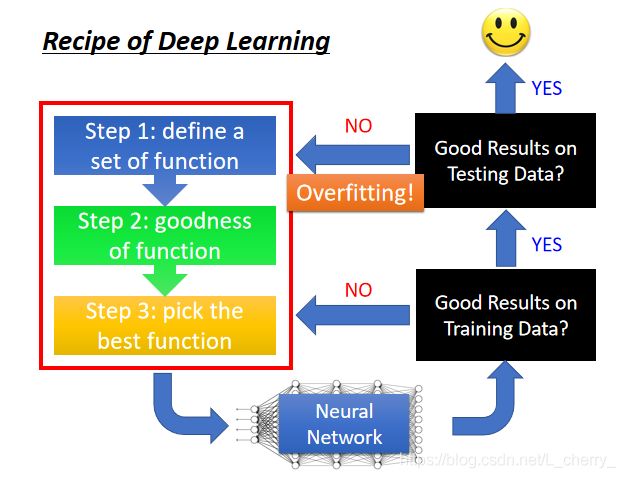
注意:并不是所有不好的performance都是overfitting。
解决Deep learning针对两个问题:一是Training data结果不好,二是Testing data结果不好;
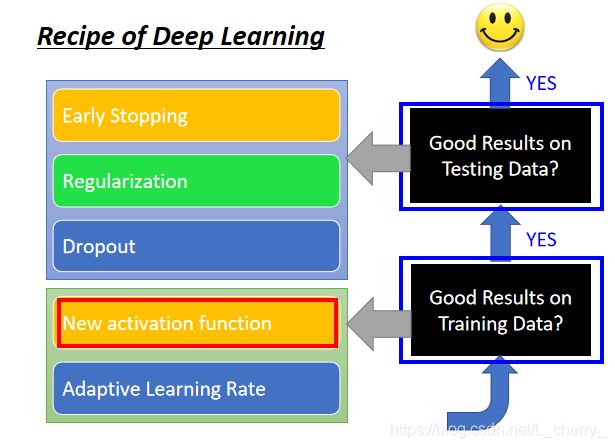
(一)针对training data进行改善
1. New activation function–针对training data,更换新的激活函数
举例:使用sigmoid function解决手写识别问题会在training data上有不好的结果,出现了vanishing gradient problem:
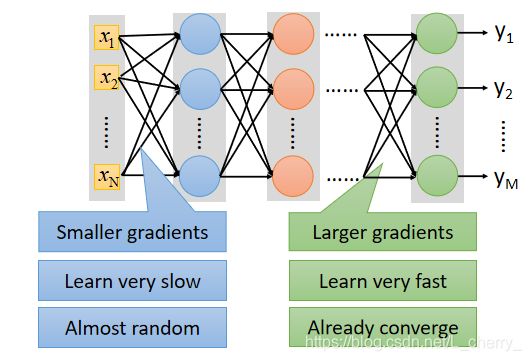
这是由于在input修改参数,每通过sigmoid function,变化就衰减一次,network越深,衰减次数越多,直到最后对output影响是非常小的,因此对cost的影响也很小。
解决办法:ReLU(Rectified Linear Unit线性整流单元)
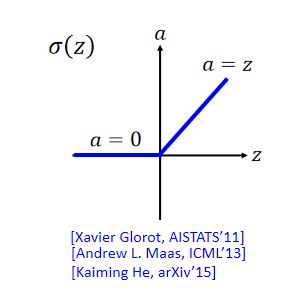
选择ReLU的理由:(1)比较快;(2)生物理由;(3)等同于无穷多的sigmoid function叠加的结果;(4)可以解决vanishing gradient problem。
解决vanishing gradient problem:当把不影响结果的neuron去掉,整个network就变成一个瘦长的linear network,就不存在递减的问题(当input变化较大时整个network就是nonlinear的;)
ReLU变体(解决ReLU不可微问题):
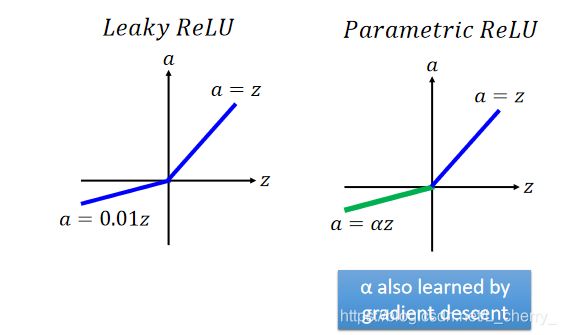
ReLU is a special cases of Maxout.
Maxout(可学习激活函数):将一组input乘上不同的weight得到不同的value,将这些value组队(组队方式事先决定),在同一个组中选择最大的value作为output。

Maxout可以模仿ReLU:
假设ReLU的neuron,input为 x x x,weight为 w w w,bias为 b b b,通过ReLU函数后得到 a a a,那么 a a a和 z z z分别与 x x x的关系为:
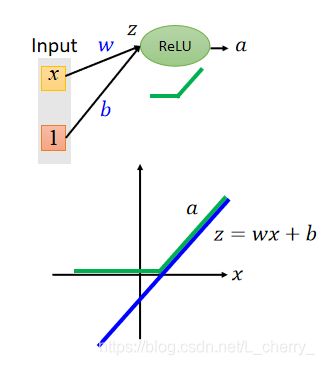
假设Maxout的neuron,input为 x x x,weight为 w w w和0,bias为 b b b和0,通过Maxout函数后得到 a a a,那么 a a a和 z 1 , z 2 z_1,z_2 z1,z2分别与 x x x的关系为:

但是,Maxout还可以做出不同于ReLU的式子,假设Maxout的neuron,input为 x x x,weight为 w w w和 w ′ w' w′,bias为 b b b和 b ′ b' b′,通过Maxout函数后得到 a a a,那么 a a a和 z 1 , z 2 z_1,z_2 z1,z2分别与 x x x的关系为:
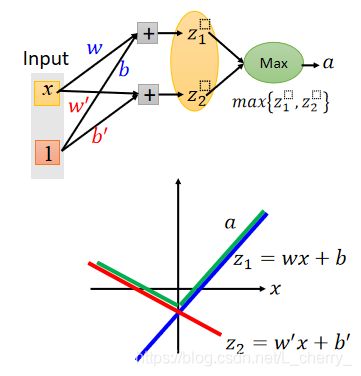
Maxout的样子是由参数 w w w和 b b b决定的,因此Maxout是一个Learnable Activation Function(可学习激活函数)。
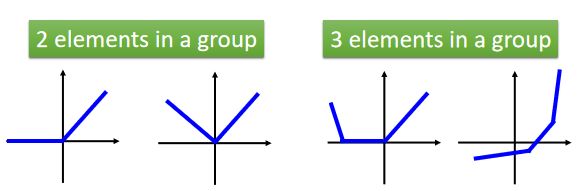
Maxout函数:(1)可以做出任何的piecewise linear convex function(分段线性凸函数);(2)多少段取决于一个group里有多少元素:
如何去train Maxout?
给一组training data x x x,假设我们知道哪一个 z z z将会是最大的:
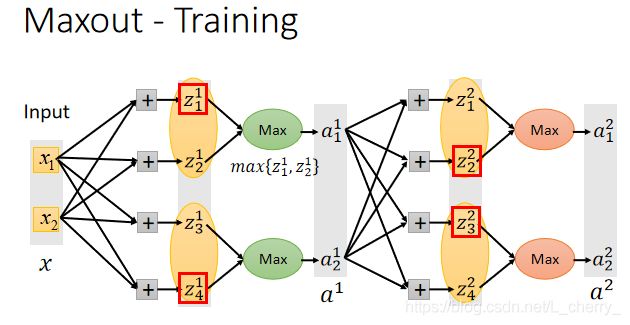
将不影响output的element拿掉就会得到比较细长的线性的network,train的时候就是train这些留下来的element(那么没有被train到的element怎么办?实际上,给予不同的input,max值是不一样的,所以每一次给予不同的input,这个network的structure都是不一样的,每一次network的structure不断变换,直到最后element其实都能被train到)。
2. Adaptive Learning Rate–针对training data,自适应学习率
之前学到过的有:

但是在做Deep Learning时,Loss Function可以是任何形状,比如:

Adagrad进阶版–RMSProp:
其中 α \alpha α值可以自己调整,假设把 α \alpha α值设的小一点,就说明倾向于相信新的gradient的error surface的平滑或陡峭程度,比较无视旧的:

optimal network parameters问题(最优参数):
(1)可能卡在local minimum(局部极小值);
(2)可能卡在saddle point(鞍点);
(3)可能卡在plateau;
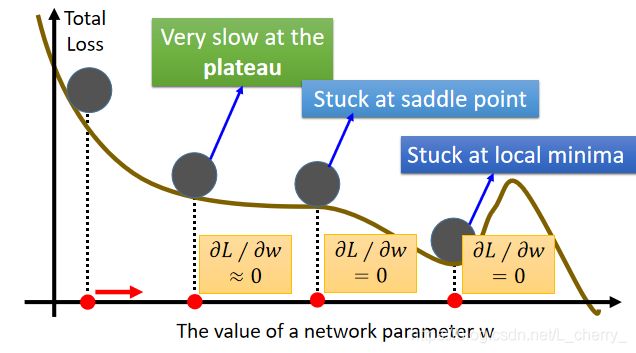
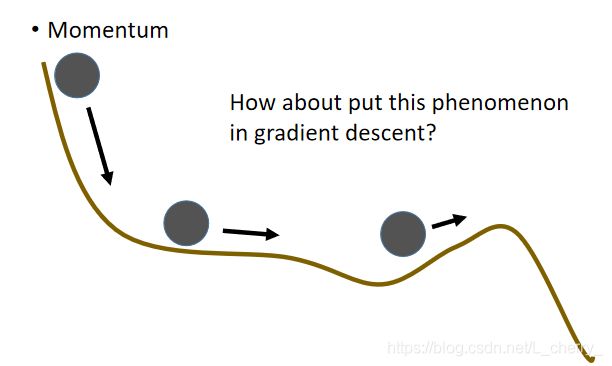
如何解决上述问题?
把Momentum(动量,惯性)引入gradient descent。
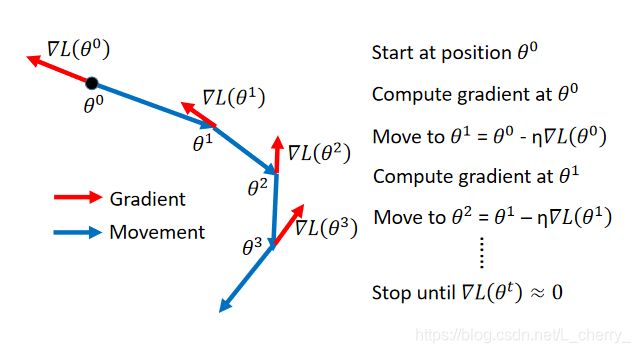
传统的gradient方法:
引入momentum的gradient方法:
Movement :movement of last step minus gradient at present(前一个时间点移动的方向,用 v v v表示),初始时,前一个时间点移动的方向 v 0 v^0 v0=0:
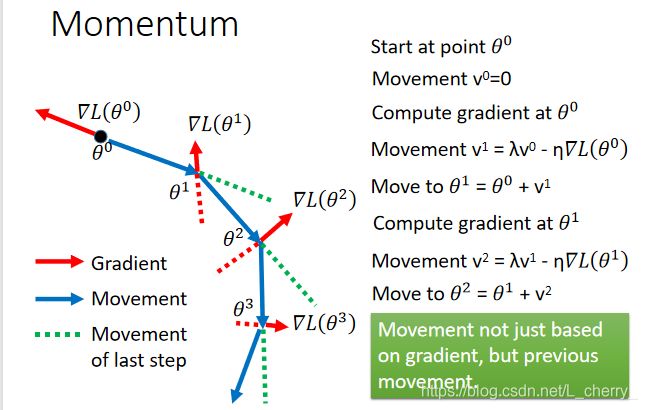
实际上, v i v^i vi是过去所有gradient的总和:
v 0 = 0 v^0 =0 v0=0;
v 1 = − η ▽ L ( θ 0 ) v^1 = -\eta \triangledown L (\theta ^0) v1=−η▽L(θ0);
v 2 = − λ η ▽ L ( θ 0 ) − η ▽ L ( θ 1 ) v^2 = -\lambda \eta \triangledown L(\theta ^0)-\eta \triangledown L (\theta ^1) v2=−λη▽L(θ0)−η▽L(θ1);…
以下通过图示表示加入momentum后是怎么运作的(其中Negative of ∂ L / ∂ w \partial L/\partial w ∂L/∂w 表示gradient方向):

由于惯性的作用在gradient为0的地方,仍旧可以往右走,甚至上坡时在惯性作用足够大时也有继续往右的可能。
总结:以上几种optimizer优化器:Adagrad、RMSProp 、Adam。
(二)针对testing data进行改善(在training data上得到好的结果,在testing data上得到不太好的结果)
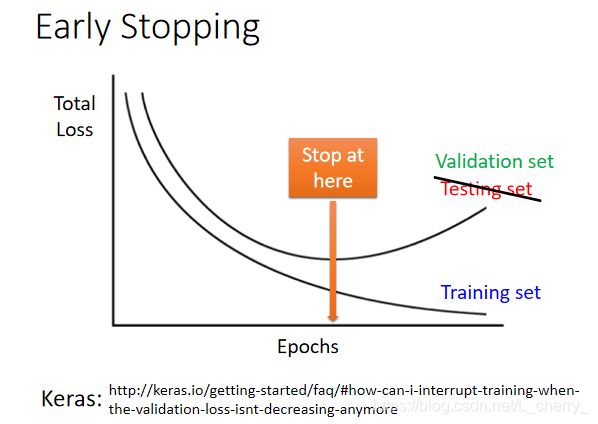
1. Early Stopping–针对testing data
停在testing data的total loss最小的地方(而不是training data最小的地方),由于我们无法预知testing data的total loss,即可用validation set来验证。
2. Regularization–针对testing data,正则化,重新定义loss function
重新定义loss function使得损失最小化:
将原来的损失函数加上一项Regularization term(不会考虑bias,只考虑weight):
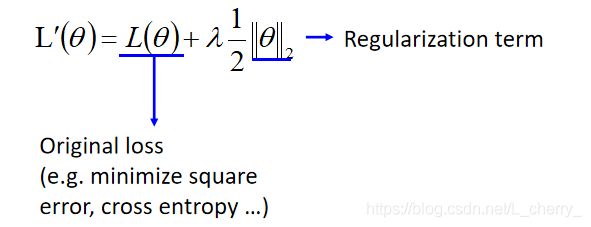
(1)这个Regularization term可以是参数的L2-Norm(范数),假设参数 θ = { w 1 , w 2 , . . . } \theta = \begin{Bmatrix} w_1,w_2,... \end{Bmatrix} θ={w1,w2,...},那么它的L2-Norm为:
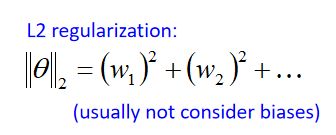
每次update时原来的 w w w都会乘于一个小于1的值( η \eta η和 λ \lambda λ的值较小,那么 1 − η λ 接 近 于 1 且 小 于 1 1-\eta\lambda接近于1且小于1 1−ηλ接近于1且小于1),那么update后就会越来越接近0,这个叫做weight decay。
(2)当设置为L1 regularization时:
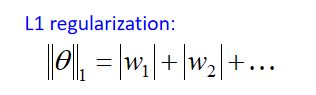
绝对值无法微分, w w w为正,微分后为1, w w w为负,微分后为-1,得到的update式子为:

L2 的结果会保留很多接近0的值,L1每次都下降一个固定的value,因此不会保留很多很小的值,得到的结果会比较sparse(稀疏)。L2的值平均都比较小,L1得到的结果有很大的值,也有很小的值。
3.Dropout–针对testing data
方法:在training 时,每一次update参数之前都对每一个neuron(包括input)进行sampling,如果这个neuron被丢掉,跟它相邻的weight也会失去作用,然后再去train,注意,每一次更新之前都得做一次samplling:
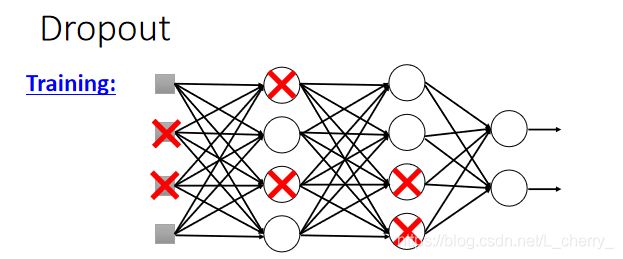

在testing时,注意两件事,(1)不做dropout;(2)如果在training时dropout rate为p%,在testing时所有的weight都要乘(1-p)%;

为什么在testing时weight需要multiply (1-p)%?
其中一种解释,在training时,由于不需要的weight被dropout了,所以导致在没有dropout的testing得到的结果会增加,因此需要更改weight的值:
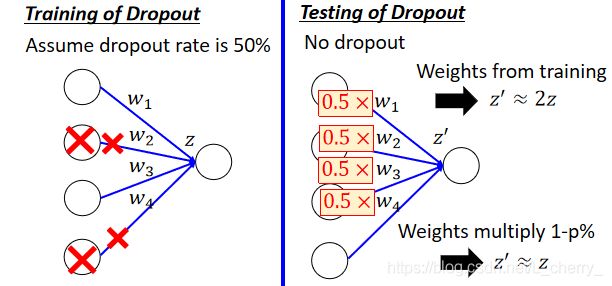
Dropout is a kind of ensemble
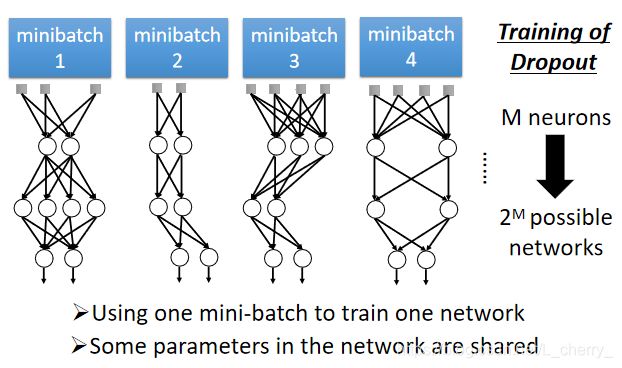
在training时,M个neuron可能会有 2 M 2^M 2M个可能的networks,每次只用一个mini-batch去train一个network,同时一些参数在这些network中是共享的。
在testing时,如果做dropout,把testing data放到那些network中去,每一个network出一个结果,把所有的结果平均起来是最后的结果,但是这样效率太低,因此在testing时不做dropout,但要把所有的weight乘上(1-p)%,然后把testing data放进去,得到最后的结果,这个结果和进行dropout后得到的结果是近似的:

为什么两者的结果近似?
假设存在一个简单的network,只有一个neuron,它的activation function是linear,不考虑bias:
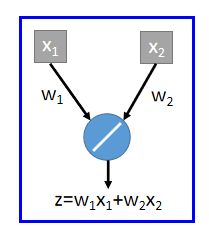
进行dropout,可能会有一下四种情况(每一个element可能会被丢掉,也可能不会):
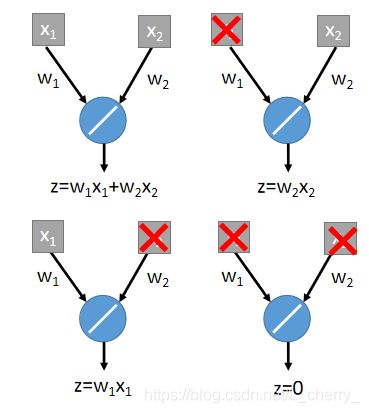
得到的结果就是所有network结果平均,即为:
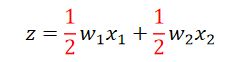
假设现在把原来的network的weight都乘 1 2 \frac{1}{2} 21,那么得到的结果为:
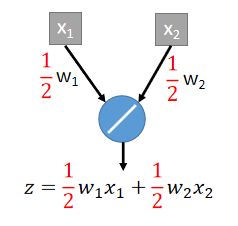
两者近似的前提是:这个network的activation function是linear的。
本文是对blibli上李宏毅机器学习2020的总结,如有侵权会立马删除。

