PyTorch框架学习十六——正则化与Dropout
PyTorch框架学习十六——正则化与Dropout
- 一、泛化误差
- 二、L2正则化与权值衰减
- 三、正则化之Dropout
- 补充:
这次笔记主要关注防止模型过拟合的两种方法:正则化与Dropout。
一、泛化误差
一般模型的泛化误差可以被分解为三部分:偏差、方差与噪声。按照周志华老师西瓜书中的定义,这三者分别如下所示:
- 偏差:度量学习算法的期望预测与真实结果的偏离程度,即刻画了学习算法本身的拟合能力。
- 方差:度量了同样大小的训练集的变动导致的学习性能的变化,刻画了数据扰动所造成的影响。
- 噪声:表达了在当前任务上任何学习算法所能达到的期望泛化误差的下界。
二、L2正则化与权值衰减
正则化是一种减小方差的策略,具体可以学习吴恩达老师的机器学习的视频。
损失函数衡量模型的输出与真实标签的差异,正则化使用的地方在目标函数,即在原来的代价函数的基础上再加上正则化项。
L2正则化的目标函数如下所示:
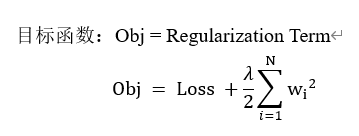
其中正则化项前的系数lambda/2,lambda调节正则化的程度,/2是为了反向传播求导的时候和平方的2可以约掉。
在反向传播进行权值更新时,无正则化项和有正则化项的更新公式如下所示:
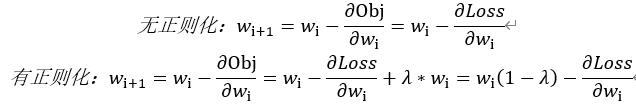
一般lambda是在0到1之间的数,所以从上图得知,有正则化时更新后的权值会比无正则化时更小一点,所以一般也将L2正则化称为权值衰减(weight decay)。
下面构建了两个相同的网络,一个没有用正则化项,一个使用了正则化项,可以观察它们各自的拟合效果:
import torch
import torch.nn as nn
import matplotlib.pyplot as plt
import sys, os
from tools.common_tools import set_seed
from torch.utils.tensorboard import SummaryWriter
set_seed(1) # 设置随机种子
n_hidden = 200 # 自定义一个全连接网络,每层200个神经元
max_iter = 2000 # 最大迭代次数2000次
disp_interval = 200 # 绘图的epoch间隔
lr_init = 0.01 # 初始化学习率
# ============================ step 1/5 数据 ============================
# 构造一批虚拟的数据
def gen_data(num_data=10, x_range=(-1, 1)):
w = 1.5
train_x = torch.linspace(*x_range, num_data).unsqueeze_(1)
train_y = w*train_x + torch.normal(0, 0.5, size=train_x.size())
test_x = torch.linspace(*x_range, num_data).unsqueeze_(1)
test_y = w*test_x + torch.normal(0, 0.3, size=test_x.size())
return train_x, train_y, test_x, test_y
train_x, train_y, test_x, test_y = gen_data(x_range=(-1, 1))
# ============================ step 2/5 模型 ============================
class MLP(nn.Module):
def __init__(self, neural_num):
super(MLP, self).__init__()
self.linears = nn.Sequential(
nn.Linear(1, neural_num),
nn.ReLU(inplace=True),
nn.Linear(neural_num, neural_num),
nn.ReLU(inplace=True),
nn.Linear(neural_num, neural_num),
nn.ReLU(inplace=True),
nn.Linear(neural_num, 1),
)
def forward(self, x):
return self.linears(x)
# 实例化两个上面构建的全连接网络,用于比较
net_normal = MLP(neural_num=n_hidden)
net_weight_decay = MLP(neural_num=n_hidden)
# ============================ step 3/5 优化器 ============================
# net_normal 无正则化,net_weight_decay 有正则化,系数为1e-2
optim_normal = torch.optim.SGD(net_normal.parameters(), lr=lr_init, momentum=0.9)
optim_wdecay = torch.optim.SGD(net_weight_decay.parameters(), lr=lr_init, momentum=0.9, weight_decay=1e-2)
# ============================ step 4/5 损失函数 ============================
loss_func = torch.nn.MSELoss()
# ============================ step 5/5 迭代训练 ============================
writer = SummaryWriter(comment='_test_tensorboard', filename_suffix="12345678")
for epoch in range(max_iter):
# forward
pred_normal, pred_wdecay = net_normal(train_x), net_weight_decay(train_x)
loss_normal, loss_wdecay = loss_func(pred_normal, train_y), loss_func(pred_wdecay, train_y)
optim_normal.zero_grad()
optim_wdecay.zero_grad()
loss_normal.backward()
loss_wdecay.backward()
optim_normal.step()
optim_wdecay.step()
if (epoch+1) % disp_interval == 0:
# 可视化
for name, layer in net_normal.named_parameters():
writer.add_histogram(name + '_grad_normal', layer.grad, epoch)
writer.add_histogram(name + '_data_normal', layer, epoch)
for name, layer in net_weight_decay.named_parameters():
writer.add_histogram(name + '_grad_weight_decay', layer.grad, epoch)
writer.add_histogram(name + '_data_weight_decay', layer, epoch)
test_pred_normal, test_pred_wdecay = net_normal(test_x), net_weight_decay(test_x)
# 绘图
plt.scatter(train_x.data.numpy(), train_y.data.numpy(), c='blue', s=50, alpha=0.3, label='train')
plt.scatter(test_x.data.numpy(), test_y.data.numpy(), c='red', s=50, alpha=0.3, label='test')
plt.plot(test_x.data.numpy(), test_pred_normal.data.numpy(), 'r-', lw=3, label='no weight decay')
plt.plot(test_x.data.numpy(), test_pred_wdecay.data.numpy(), 'b--', lw=3, label='weight decay')
plt.text(-0.25, -1.5, 'no weight decay loss={:.6f}'.format(loss_normal.item()), fontdict={'size': 15, 'color': 'red'})
plt.text(-0.25, -2, 'weight decay loss={:.6f}'.format(loss_wdecay.item()), fontdict={'size': 15, 'color': 'red'})
plt.ylim((-2.5, 2.5))
plt.legend(loc='upper left')
plt.title("Epoch: {}".format(epoch+1))
plt.show()
plt.close()
最终的拟合效果:
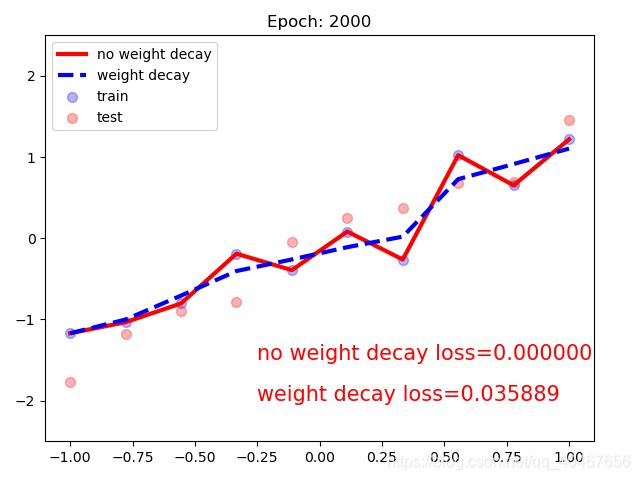
红色的线显然已经过拟合了,而蓝色的线加了正则化项,比红色的线的效果好一点,这就是L2正则化项缓解过拟合的一个举例。
因为在代码中使用了TensorBoard可视化每一网络层的权重,可以看一下有无正则化两种情况下权值分布的差异:
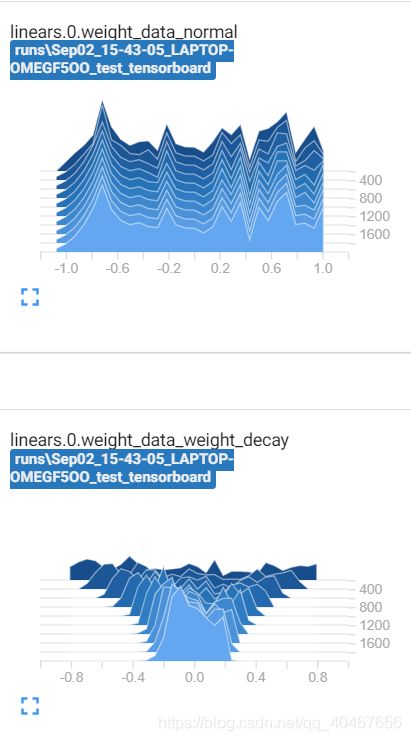
可以看出不加正则化时,权值是比较分散的,而且存在较大的值,加入正则化之后,权值的分布都集中在较小值的范围,不存在较大的权值,这也是减轻过拟合的体现。
三、正则化之Dropout
Dropout的概念发扬光大于AlexNet之中,简单来说就是对网络中的每个神经元进行随机失活。
- 随机:有一个失活概率Dropout probability。
- 失活:该神经元对应的权值为0,即该神经元不与其他神经元连接。
如下图所示就是一次随机失活的情况:
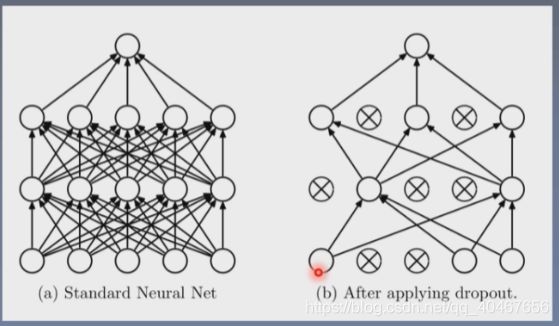
训练过程的每个epoch得到的失活后的网络都不一样,这样使得模型具有多样性,不会特别依赖某些固定的神经元,不会使得某些神经元的权重过大,缓解了过拟合的问题。
注意:Dropout是在训练过程进行随机失活,在测试的时候是恢复为原来的网络结构的,所以测试的时候,要将所有的权重乘以1-Dropout probability,以保持输入与权值相乘的结果与训练时一样大。
下面我们看一下在PyTorch中Dropout的实现:
torch.nn.Dropout(p: float = 0.5, inplace: bool = False)
然后需要注意的是,PyTorch在实现Dropout的时候,训练时权重均乘以了1/(1-p),即除以1-p,这样的话测试的时候就不用手动将所有的权重乘以1-Dropout probability了,方便了测试的过程。
用上面L2正则化的代码示例稍加修改作为Dropout的举例:
import torch
import torch.nn as nn
import matplotlib.pyplot as plt
import sys, os
from tools.common_tools import set_seed
from torch.utils.tensorboard import SummaryWriter
set_seed(1) # 设置随机种子
n_hidden = 200
max_iter = 2000
disp_interval = 400
lr_init = 0.01
# ============================ step 1/5 数据 ============================
def gen_data(num_data=10, x_range=(-1, 1)):
w = 1.5
train_x = torch.linspace(*x_range, num_data).unsqueeze_(1)
train_y = w*train_x + torch.normal(0, 0.5, size=train_x.size())
test_x = torch.linspace(*x_range, num_data).unsqueeze_(1)
test_y = w*test_x + torch.normal(0, 0.3, size=test_x.size())
return train_x, train_y, test_x, test_y
train_x, train_y, test_x, test_y = gen_data(x_range=(-1, 1))
# ============================ step 2/5 模型 ============================
class MLP(nn.Module):
def __init__(self, neural_num, d_prob=0.5):
super(MLP, self).__init__()
self.linears = nn.Sequential(
nn.Linear(1, neural_num),
nn.ReLU(inplace=True),
nn.Dropout(d_prob),
nn.Linear(neural_num, neural_num),
nn.ReLU(inplace=True),
nn.Dropout(d_prob),
nn.Linear(neural_num, neural_num),
nn.ReLU(inplace=True),
nn.Dropout(d_prob),
nn.Linear(neural_num, 1),
)
def forward(self, x):
return self.linears(x)
net_prob_0 = MLP(neural_num=n_hidden, d_prob=0.)
net_prob_05 = MLP(neural_num=n_hidden, d_prob=0.5)
# ============================ step 3/5 优化器 ============================
optim_normal = torch.optim.SGD(net_prob_0.parameters(), lr=lr_init, momentum=0.9)
optim_reglar = torch.optim.SGD(net_prob_05.parameters(), lr=lr_init, momentum=0.9)
# ============================ step 4/5 损失函数 ============================
loss_func = torch.nn.MSELoss()
# ============================ step 5/5 迭代训练 ============================
writer = SummaryWriter(comment='_test_tensorboard', filename_suffix="12345678")
for epoch in range(max_iter):
pred_normal, pred_wdecay = net_prob_0(train_x), net_prob_05(train_x)
loss_normal, loss_wdecay = loss_func(pred_normal, train_y), loss_func(pred_wdecay, train_y)
optim_normal.zero_grad()
optim_reglar.zero_grad()
loss_normal.backward()
loss_wdecay.backward()
optim_normal.step()
optim_reglar.step()
if (epoch+1) % disp_interval == 0:
net_prob_0.eval()
net_prob_05.eval()
# 可视化
for name, layer in net_prob_0.named_parameters():
writer.add_histogram(name + '_grad_normal', layer.grad, epoch)
writer.add_histogram(name + '_data_normal', layer, epoch)
for name, layer in net_prob_05.named_parameters():
writer.add_histogram(name + '_grad_regularization', layer.grad, epoch)
writer.add_histogram(name + '_data_regularization', layer, epoch)
test_pred_prob_0, test_pred_prob_05 = net_prob_0(test_x), net_prob_05(test_x)
# 绘图
plt.clf()
plt.scatter(train_x.data.numpy(), train_y.data.numpy(), c='blue', s=50, alpha=0.3, label='train')
plt.scatter(test_x.data.numpy(), test_y.data.numpy(), c='red', s=50, alpha=0.3, label='test')
plt.plot(test_x.data.numpy(), test_pred_prob_0.data.numpy(), 'r-', lw=3, label='d_prob_0')
plt.plot(test_x.data.numpy(), test_pred_prob_05.data.numpy(), 'b--', lw=3, label='d_prob_05')
plt.text(-0.25, -1.5, 'd_prob_0 loss={:.8f}'.format(loss_normal.item()), fontdict={'size': 15, 'color': 'red'})
plt.text(-0.25, -2, 'd_prob_05 loss={:.6f}'.format(loss_wdecay.item()), fontdict={'size': 15, 'color': 'red'})
plt.ylim((-2.5, 2.5))
plt.legend(loc='upper left')
plt.title("Epoch: {}".format(epoch+1))
plt.show()
plt.close()
net_prob_0.train()
net_prob_05.train()
做的修改就是网络模型里加入了Dropout层,删去了L2正则化项,然后实例化了两个模型,一个失活概率为0,即等效为不加Dropout层,一个失活概率为0.5,即加入Dropout层,将这两个模型进行数据拟合,观察结果如下:
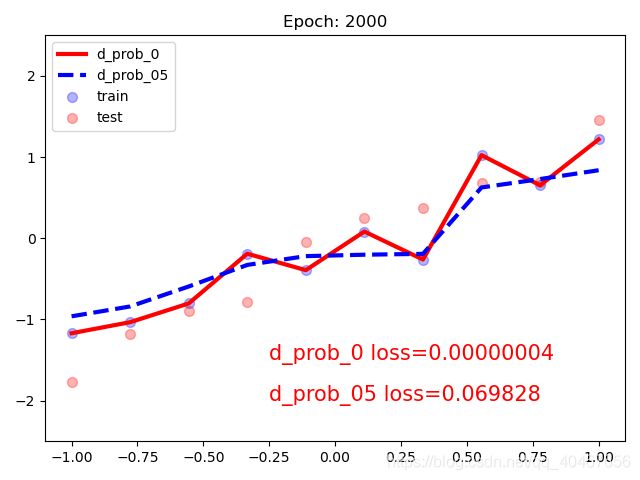
也可以看出,Dropout层的加入也一定程度上缓解了过拟合。
同样,我们也来看一下这时的权值分布,因为第一层是输入层,没有加Dropout层,所以我们看第三层的权值分布(第二层为ReLU层):
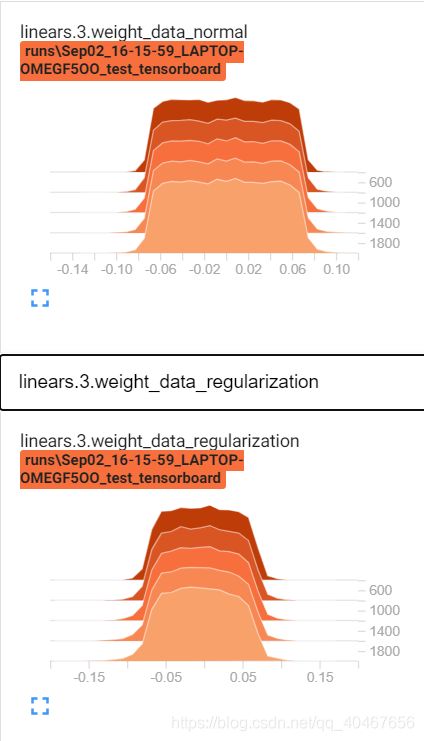
也有类似的作用——收缩权重。
补充:
在使用Dropout层,以及后面要讲的BN层这些东西时,还有一个需要注意的小细节,因为这些层在训练模式和测试模式是有差别的,所以在不同时刻需要切换模式,用到的就是上面代码中的
net_prob_0.eval()
net_prob_05.eval()
以及:
net_prob_0.train()
net_prob_05.train()