BP神经网络设计与实现
BP神经网络设计与实现
实验要求
基于Python原生实现,不调用深度学习框架函数,完成代码编写
实验内容
1、详细论述本次实验的算法设计及描述。
2、双月数据构建生成及使用方法。
3、根据误差反向传播计算准则,生成双月数据分类结果,并进行可视化展示,主要分以下部分开展实验:
(1)根据初始权重参数不同,对实验结果进行展示分析。
(2)根据网络结构不同,对实验结果进行展示分析。
(3)根据学习率不同,对进行实验结果进行展示分析。
(4)根据激活函数不同,对实验结果进行展示分析。
详细过程
一、算法设计及描述
本次实验主要是通过BP神经网络对双月数据进行分类,即通过BP反向传播算法实现二分类,算法设计思路如下:
-
通过numpy库构建双月数据,并生成矩阵数据
-
将上半月标记为1,下半月标记为-1,即转化为二分类问题
-
初始化网络中的权值,偏置项如下:
# 初始化权重,随机设置,范围为(-1,1) #输入层3个节点,隐藏层50个节点 V = np.random.random((3, 50)) * 2 - 1 W = np.random.random((50, 1)) * 2 - 1 #偏置 b1=0.5*np.ones((200,50)) #输入层到隐藏层偏置 b2=0.5*np.ones((200,1)) #隐藏层到输出层偏置4.激活前向传播,得到各层输出和损失函数的期望值
#向前传播 L1 = sigmoid(np.dot(X, V)+b1) # L1:输入层传递给隐藏层的值; L2 = sigmoid(np.dot(L1, W)+b2) # L2:隐藏层传递到输出层的值;输出层1个节点 L2_delta = (Y.T - L2) * dsigmoid(L2) # L2_delta:输出层的误差信号 L1_delta = L2_delta.dot(W.T) * dsigmoid(L1) # L1_delta:隐藏层的误差信号5.根据损失函数,计算输出单元的误差项和隐藏单元的误差项,并更新权值和偏置项
# W_C:输出层对隐藏层的权重改变量 # V_C:隐藏层对输入层的权重改变量 W_C = lr * L1.T.dot(L2_delta) V_C = lr * X.T.dot(L1_delta) #权重更新 W = W + W_C V = V + V_C6.重复步骤2-4,直到损失函数小于事先给定的阈值或迭代次数用完为止。
for i in range(20000): update() # 更新权值 if i % 500 == 0: L1 = sigmoid(np.dot(X, V)) # 隐藏层输出 L2 = sigmoid(np.dot(L1, W)) # 输出层输出 print('当前误差:', np.mean(np.abs(Y.T - L2))) num_MSE.append(np.mean(np.abs(Y.T - L2))) num_step.append(i)7.输出最终的参数即为最佳参数,然后根据训练好的网络对双月数据重新分类,计算准确率
#根据训练好的网络对双月数据重新分类,计算准确率 #前向传播 L1 = sigmoid(np.dot(X, V)+b1) # 隐藏层输出 L2 = sigmoid(np.dot(L1, W)+b2) # 输出层输出 list1 = [] for i in map(judge, L2): list1.append(i) #将分类结果置于list1 print(list1) coun = 0 for i in range(len(list1)): if list1[i] == y[i]: coun += 1 print("准确率:", coun/200)8.通过训练好的网络构造预测函数,并画出决策边界
#预测函数 def predict(X): b=np.ones((1,50)) L1 = tanh(np.dot(X, V)+b) L2 = tanh(np.dot(L1, W)) y=judge(L2) return y for x in np.arange(-15., 25., 0.1): for y in np.arange(-10., 10., 0.1): X=np.array([[x,y]]) y_p = predict(X) if (y_p_old < 0 and y_p > 0):#找出临界点 test_x.append(x) test_y.append(y) y_p_old = y_p # 画决策边界 plt.subplot(211) plt.plot(x1, y1, 'r*', x2, y2, 'b*',test_x, test_y, 'g--') plt.show()
二、双月数据构建生成及使用方法。
实现条件:
-
假设上半月固定不动
-
下半月的圆心可随着d的不同以及r的不同而调整
-
上半月和下半月半径相同
-
半径r表示各自圆心到半圆环中部的位置
半圆的生成:
1 、半径: r U ( r − w / 2 , r + w / 2 ) ( 均匀分布 ) 1、半径:r~U(r-w/2,r+w/2)(均匀分布) 1、半径:r U(r−w/2,r+w/2)(均匀分布)
2 、上半月: θ U ( 0 , π ) 下半月: θ U ( − π , 0 ) 2、上半月:θ~U(0,π) 下半月:θ~U(-π,0) 2、上半月:θ U(0,π)下半月:θ U(−π,0)
import numpy as np
import matplotlib.pyplot as plt
import math
# 构建双月数据
def dbmoon(N=100, d=2, r=10, w=2):
N1 = 10*N
w2 = w/2
done = True
data = np.empty(0)
while done:
# 生成矩阵数据
tmp_x = 2*(r+w2)*(np.random.random([N1, 1])-0.5)
tmp_y = (r+w2)*np.random.random([N1, 1])
tmp = np.concatenate((tmp_x, tmp_y), axis=1)
tmp_ds = np.sqrt(tmp_x*tmp_x + tmp_y*tmp_y)
# 生成双月数据
idx = np.logical_and(tmp_ds > (r-w2), tmp_ds < (r+w2))
idx = (idx.nonzero())[0]
if data.shape[0] == 0:
data = tmp.take(idx, axis=0)
else:
data = np.concatenate((data, tmp.take(idx, axis=0)), axis=0)
if data.shape[0] >= N:
done = False
print(data)
db_moon = data[0:N, :]
print(db_moon)
data_t = np.empty([N, 2])
data_t[:, 0] = data[0:N, 0] + r
data_t[:, 1] = -data[0:N, 1] - d
db_moon = np.concatenate((db_moon, data_t), axis=0)
return db_moon
三、根据误差反向传播计算准则,生成双月数据分类结果,并进行可视化展示,主要分以下部分开展实验:
(1)根据初始权重参数不同,对实验结果进行展示分析。
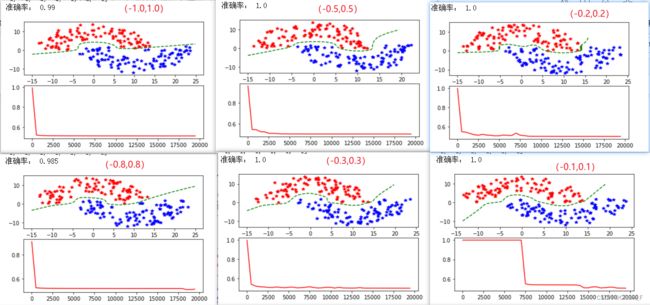
本部分主要以sigmod为激活函数,学习率设为0.05,网络结构为3-50-1,本实验中初始权重都设置为随机生成,以不同范围初始权重为变量讨论对结果的影响:
初始权重范围分别设为了(-1.0,1.0),(-0.8,0.8),(-0.5,0.5),(-0.3,0.3),(-0.2,0.2),(-0.1,0.1)
经过实验结果分析,选取6中不同范围的初始权重进行实验,得出的分类效果都比较好,由此可分析出,初始权重对神经网络的最终学习结果影响不大,但会影响训练收敛速度。
(2)根据网络结构不同,对实验结果进行展示分析。
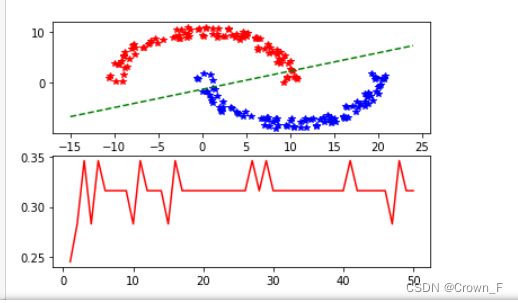
首先分析单层传感器的分类效果,选择激活函数为符号函数,只有输入和输出两层:
可见单层传感器只能进行线性划分,对于这种非线性数据,肉眼可见分类效果很不好。
其次以三层网络为例
本部分主要以sigmoid为激活函数,学习率设为0.1,网络结构为3-n-1,本实验中初始权重都设置为随机生成,范围在(-1.0,1.0)以隐藏层节点数为变量讨论对结果的影响:
由此可见网络越简单,训练效果越差,网络越复杂,训练效果越好,但并不是网络越复杂越好,网络太复杂也容易陷入局部极小值,使训练结果出现极端情况。
为体现对比效果,另取tanh做激活函数,学习率设为0.1,网络结构为3-50-1,2-50-1,本实验中初始权重都设置为随机生成,范围在(-1.0,1.0),以两种网络结构为变量讨论对结果的影响:
(3)根据学习率不同,对进行实验结果进行展示分析。
本部分主要以sigmoid为激活函数,网络结构为3-20-1,本实验中初始权重都设置为随机生成,范围在(-1.0,1.0)以学习率为变量讨论对结果的影响:

由实验结果分析,当学习率>=0.5时,网络很难收敛,很难找到最优值,当学习率在0.03-0.1之间效果都比较好,但如果学习率设置太小的话,网络收敛速度会变慢,而且有出现陷入局部极值情况。
(4)根据激活函数不同,对实验结果进行展示分析。
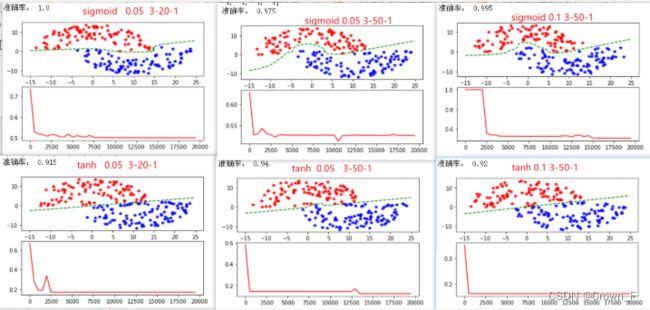
本部分设置学习率为0.05,网络结构为3-20-1,本实验中初始权重都设置为随机生成,范围在(-1.0,1.0),激活函数主要选取sigmoid和tanh两种:
Tanh的诞生比Sigmoid晚一些,sigmoid函数我们提到过有一个缺点就是输出不以0为中心,使得收敛变慢的问题。而Tanh则就是解决了这个问题。Tanh就是双曲正切函数。等于双曲余弦除双曲正弦。
但经过实际实验发现,在此分类模型中,以sigmoid做激活函数的分类效果比以tanh做激活函数的分类效果要好。
实验总结
BP神经网络无论在网络理论还是在性能方面已比较成熟。其突出优点就是具有很强的非线性映射能力和柔性的网络结构。网络的中间层数、各层的节点个数可自己设定,并且随着结构的差异有不同的效果。但是BP神经网络也有一些缺陷。
- 学习速度慢,即使是一个简单的问题,一般也需要几百次甚至上千次的学习才能收敛。
- 容易陷入局部极小值,这个很让人头疼,如果参数设置的不合适,在实验过程中会经常遇到这种情况。
- 怎样选择网络层数、各层节点个数才能使训练效果达到最好是不清楚的。
实验感悟
BP神经网络无论在网络理论还是在性能方面已比较成熟。其突出优点就是具有很强的非线性映射能力和柔性的网络结构。网络的中间层数、各层的节点个数可自己设定,并且随着结构的差异有不同的效果。但是BP神经网络也有一些缺陷。
- 学习速度慢,即使是一个简单的问题,一般也需要几百次甚至上千次的学习才能收敛。
- 容易陷入局部极小值,这个很让人头疼,如果参数设置的不合适,在实验过程中会经常遇到这种情况。
- 怎样选择网络层数、各层节点个数才能使训练效果达到最好是不清楚的。